Scienza greco-romana. Tolomeo
Scienza greco-romana. Tolomeo
Tolomeo
L'indagine scientifica
Di Claudio Tolomeo si sono conservate numerose opere, che nel loro insieme coprono un ampio settore dell'enciclopedia del sapere del II sec. d.C. La sua importanza e la sua fama nella storia della scienza sono dovute principalmente agli scritti di astronomia, in primo luogo all'Almagesto (Syntaxis mathematica), oltre al quale ci restano altri cinque testi più brevi della stessa area, ossia le Tavole manuali, le Ipotesi planetarie, il Planisfero, l'Analemma e le Fasi delle stelle fisse; di lui abbiamo anche trattazioni complessive di astrologia, quale la Tetrabiblos, di musicologia, quale gli Armonici, di geografia, quale la Geografia, e di teoria della visione, l'Ottica; ci resta infine un suo breve scritto di carattere filosofico, Il criterio e l'egemonico.
Della vita di Tolomeo sappiamo soltanto quanto si può ricavare dai suoi scritti: operò ad Alessandria d'Egitto, alla cui Biblioteca dovette certamente attingere per la grandissima quantità di materiale documentario presente nelle sue opere. Le osservazioni astronomiche personali, di cui riferisce nell'Almagesto, vanno dal 127 al 141; la pubblicazione di quest'opera va collocata alcuni anni dopo, non pochissimi, data la sua mole e la quantità degli argomenti trattati. Dopo l'Almagesto Tolomeo deve essere vissuto ancora a lungo, visto che sono successivi a tale opera molti altri suoi scritti, tutti contenenti ricerche impegnative e lunghe: certamente le Tavole manuali, le Ipotesi planetarie, la Tetrabiblos, la Geografia e, molto probabilmente, l'Ottica (quest'ultima presumibilmente posteriore anche alle Ipotesi planetarie). Le altre sue opere rimasteci non sono collocabili cronologicamente con sicurezza. Considerato che Tolomeo non poteva essere molto giovane nel 127, si può dire che nacque intorno al 100, che la pubblicazione dell'Almagesto avvenne all'incirca nel 150 e che la sua morte avvenne verosimilmente poco dopo il 170.
Due aspetti consentono di delimitare il settore dell'enciclopedia scientifica a lui contemporanea, nel quale si colloca la sua produzione scientifica. Da una parte, si tratta sempre di aree di indagine passibili di rilevanti applicazioni matematiche; le cose che sono ‒ dice Tolomeo nel proemio dell'Almagesto ‒ sono costituite da forma, materia e mutamento, e rientrano nel campo di indagine che è chiamato 'matematico' tutte le qualità formali delle cose: la figura, il numero, la grandezza, cui aggiunge il luogo e il tempo e associa inoltre i moti locali (I, 1). In tutte le sue opere sopra citate la trattazione contiene una notevole componente matematica, seppure in una misura che varia di volta in volta. Dall'altra parte, nel loro insieme le sue opere convergono nell'elaborazione di una cosmologia, il cui tratto saliente è dato dalla netta separazione tra cielo e Terra, cui è associata una caratterizzazione del cielo come divino, costituito da una materia speciale, l'etere, e perciò oggetto privilegiato di una trattazione matematica. Una cosmologia siffatta è presente sullo sfondo dell'Almagesto, è più in primo piano nelle Ipotesi planetarie e nella Tetrabiblos ed è ripresa nelle pagine finali degli Armonici. Gli aspetti matematici delle cose che sono e la loro integrazione in un tale quadro cosmologico costituiscono dunque i due centri dell'attenzione delle indagini scientifiche di Tolomeo.
In generale, nelle opere di Tolomeo si avverte l'intento di esaurire l'intero specifico campo di indagine considerato, senza omettere nulla; le più ampie hanno in effetti l'impianto di manuali e in esse è sempre trattata una quantità molto grande di fenomeni ed è sempre presente l'intento di riorganizzare in modo coerente l'insieme. Tolomeo quasi certamente non si pensò come uno scienziato che innova, trovando vie di ricerca mai percorse prima, ma piuttosto come un uomo di scienza che si situa in una tradizione, la elabora, eventualmente la corregge e ne sviluppa le parti non compiute. Egli sottolinea nell'Almagesto il suo debito verso Ipparco di Nicea (II sec. a.C.); e un rapporto analogo con i predecessori si può intravedere, nonostante le carenze della nostra documentazione, anche nella Geografia, nell'Ottica e negli Armonici; soltanto in quest'ultima opera ‒ scritta in presenza di due tradizioni musicologiche rivali, a ciascuna delle quali Tolomeo imputa carenze metodologiche specifiche ‒ emerge in certa misura, ma senza enfasi, il senso di una sua originalità. Ciò, d'altronde, non gli impedì di essere di fatto originale in punti anche molto importanti; basti citare, in ottica, il collegamento tra le analisi geometriche e le considerazioni fisiologiche e, soprattutto, in astronomia l'introduzione dell''equante' nel fronteggiare le difficoltà connesse a un trattamento fine dei moti planetari (dove sono originali anche i procedimenti di calcolo adottati).
Nelle sue opere maggiori, dato il loro carattere di manuale scientifico, è presente una forte attenzione didattica, uno sforzo di cominciare dal principio, cioè dai fenomeni più radicati nell'esperienza percettiva di tutti, più evidenti e irrecusabili, e di lasciare in vista i passi compiuti. In questo modo esse furono lette e considerate per molti secoli, con differente fortuna, in conseguenza non soltanto della loro intrinseca vitalità scientifica, ma anche delle vicende della loro trasmissione. Grande fortuna conobbe non soltanto l'Almagesto ‒ l'opera fondamentale dell'astronomia matematica fino a Copernico compreso ‒ ma anche la Tetrabiblos, mentre, per esempio, l'Ottica fu probabilmente la prima a morire scientificamente (in conseguenza dei risultati delle ricerche di Ibn al-Hayṯam ‒ l'Alhazen dei medievali, m. nel 1039 ‒, che pure era stato influenzato molto fortemente da Tolomeo).
L''Almagesto'
Il titolo originale dei tredici libri di cui consta la grande opera astronomica di Tolomeo fu Mathēmatikḕ sýntaxis, 'trattazione matematica', dove 'matematica' va inteso in senso molto ampio, comprensivo anche di 'astronomica'; essa fu chiamata in seguito la 'grande' o la 'grandissima' (megístē) trattazione, e la doppia storpiatura di questo termine nelle traduzioni latino-medievali delle traduzioni arabe ha fatto sì che divenisse l'Almagesto.
Il Libro I ha carattere preliminare. Come di norma per un'introduzione, la prima metà (capp. I-VIII) è stata certamente redatta alla fine del lavoro e in essa Tolomeo riesamina le ipotesi più generali che reggono la sua astronomia: il cielo è sferico (I, 3), la Terra per la percezione astronomica è sferica (I, 4) ed è grande come un punto rispetto al cielo (I, 6), si trova al centro (I, 5) e vi resta immobile (I, 7); si aggiunge la distinzione, ormai antica e notissima, tra i due principali moti celesti, quello diurno e quello eclitticale (I, 8). La sezione è motivata con una considerazione didattica: è opportuno "tenere nella memoria" (I, 2) tali ipotesi. Queste sono inizialmente ricavate dai fenomeni più evidenti e indubitabili, e forniscono soltanto per grandi linee il quadro d'insieme preliminare del campo d'indagine, cioè del cielo (I, 9); esse saranno definitivamente confermate dall'accordo con i fenomeni che si avrà nelle indagini particolari, cioè quelle sui diversi fenomeni planetari (I, 8). Qui dunque Tolomeo adduce argomentazioni molto generali, che riprendono discussioni anche di secoli addietro. Fin dove è possibile, il punto delle sue argomentazioni è che queste ipotesi sono in accordo con i fenomeni più evidenti, ed esse soltanto lo sono.
Quanto poi all'ipotesi che la Terra non compia nessun movimento, essa è confermata scomponendo l'ipotesi opposta in due e rigettando l'una e l'altra separatamente (I, 7); in entrambi i casi, considerazioni di compatibilità con i fenomeni si combinano con considerazioni fisiche. Che la Terra si muova allontanandosi dal centro, come cadendo in una direzione, è anzitutto contrario ai fenomeni, dunque va respinto come impossibile; Tolomeo aggiunge poi considerazioni fisiche che spiegano il permanere della Terra al centro rifacendosi alla fisica di Aristotele. Non c'è invece incompatibilità con i fenomeni per quanto riguarda l'ipotesi che la Terra si muova restando al centro e ruotando su un asse coincidente con quello dei poli celesti; qui il rifiuto si basa esclusivamente su ragioni fisiche; precisamente, se la Terra ruotasse su sé stessa i corpi sulla sua superficie dovrebbero sempre essere lasciati indietro dal suo moto, a meno di ulteriori supposizioni assurde, come quella che l'aria ruoti insieme alla Terra e i corpi sulla Terra siano "come unificati" all'aria.
La discussione tolemaica merita due osservazioni. La prima è che l'ipotesi di un moto rotatorio della Terra qui considerata è quella 'geocentrica' di Eraclide Pontico (IV sec. a.C.), per la quale la Terra resta al centro della rotazione sia del Sole sia di tutti i pianeti, e non quella eliocentrica, né nella versione completa ‒ per la quale il Sole immobile è il centro della rotazione sia della Terra sia dei pianeti ‒ né in una versione soltanto parziale (quale probabilmente fu quella formulata da Aristarco di Samo nel III sec. a.C.). L'eliocentrismo non è considerato in questo passo (né Tolomeo lo considera mai) e la scelta è tra due versioni del geocentrismo. La scelta che a noi postcopernicani appare critica non è qui considerata dall'indagine di Tolomeo; a buon diritto, egli può ritenere astronomicamente irrilevante la tesi che rigetta, perché nella teoria dei moti planetari non cambierebbe nulla. Questo porta alla seconda osservazione (nella quale si anticipa un punto che sarà ripreso più avanti, nel par. 3); il fatto che Tolomeo si curi di confutare l'ipotesi eraclidea indica quale fosse la sua mira in questa discussione. Egli vuole per la sua astronomia matematica ipotesi vere, e non semplicemente adeguate per la 'salvezza dei fenomeni', visto che altrimenti si sarebbe limitato a vagliare la compatibilità con i fenomeni delle diverse ipotesi di un movimento della Terra; perciò l'argomentazione verte in generale sul problema se la Terra si muova, ed egli introduce ragioni fisiche, in particolare là dove non dispone di un'altra via per decidere, data l'equivalenza immediata dell'ipotesi eraclidea con la sua.
Alla sezione introduttiva fa seguito una prevalentemente matematica, in cui è dimostrato il cosiddetto 'teorema di Tolomeo', in base al quale diviene possibile produrre una tavola delle corde ‒ l'unica funzione trigonometrica considerata dagli antichi ‒ per intervalli molto piccoli, di mezzo grado (I, 10-11). Tolomeo presume nel suo lettore soltanto la conoscenza della geometria euclidea; sulla base di questa, mediante le tavole trigonometriche, sarà compiuto tutto il lavoro di produzione dei modelli e di determinazione dei loro parametri astronomicamente rilevanti.
L'Almagesto contiene essenzialmente una teoria dei moti planetari, che mira a rendere possibile la previsione della posizione in cui si troverà un astro per qualsiasi momento del tempo; la validità della teoria è provata dalla giustezza delle previsioni. L'esposizione si articola in quattro sezioni, che si succedono in quest'ordine: (1) il Sole (Lib. III), (2) la Luna (Libb. IV-VI), (3) le stelle fisse (Libb. VII-VIII), (4) i cinque pianeti allora conosciuti, cioè Mercurio, Venere, Marte, Giove, Saturno (Libb. IX-XIII). Non si tratta di una sequenza arbitraria: la teoria della Luna richiede il calcolo delle posizioni del Sole; la mappatura delle stelle fisse è compiuta, per alcune stelle di cruciale importanza, servendosi della Luna come di una sorta di marcatore; la teoria dei cinque pianeti si serve in molti casi di osservazioni fatte in riferimento a certe stelle fisse e inoltre richiede anch'essa il calcolo delle posizioni del Sole. Ogni sezione si serve dunque di esiti delle sezioni che la precedono. C'è anche una certa crescita nella complessità, in particolare nel passaggio dal Sole alla Luna e ai cinque pianeti, ma il grado di complessità è un criterio soltanto parziale di organizzazione del testo; in effetti, tra i cinque pianeti il primo a essere trattato è Mercurio, il più vicino a noi, che pure è quello che richiederà il modello più complicato.
Le diverse e successive sezioni sul Sole, sulla Luna e sui pianeti presentano poi ciascuna una sequenza interna, che nelle sue linee generali si ripete. Essa è scandita fondamentalmente in sette passi: (1) produzione dei valori numerici delle periodicità principali dell'astro; (2) produzione delle tavole dei moti medi per le periodicità presentate nel primo passo; (3) presentazione e discussione dei modelli geometrico-cinematici adottati per ciascun astro; (4) derivazione dei valori numerici di quei parametri dei modelli adottati, in base ai quali si potranno calcolare le posizioni vere; (5) controlli ed eventuali complicazioni nel modello adottato e produzione del modello finale, dotato dei valori numerici finali; (6) produzione delle tavole delle 'equazioni' (come le chiameranno i medievali), in base alle quali si possono calcolare le posizioni vere dell'astro per ogni momento; (7) istruzioni per il calcolo.
Il passo (5) è assente per il Sole (il quale non richiede complicazioni per il suo modello). La sequenza dei passi (3), (4) e (5) è nitidamente visibile soltanto nel caso della Luna e tuttavia è sicuramente sottesa anche alla trattazione dei pianeti. In questa delineazione delle teorie planetarie ci limiteremo alla parte principale, cioè la teoria dei moti in longitudine, che da sola occupa una buona metà dell'Almagesto (ignorando le complicazioni apportate dalla precessione degli equinozi, la teoria delle eclissi e quella degli spostamenti in latitudine). Una esposizione scomposta e scandita secondo i passi della sequenza comune consentirà di far vedere nel modo più chiaro come in generale Tolomeo procede.
Nello studio dei moti in longitudine i periodi chiave sono quello cosiddetto 'tropico', cioè del ritorno dell'astro alla stessa longitudine, e quello detto 'anomalistico', ossia del ritorno dell'astro alla stessa velocità, riguardo al quale è da notare che il termine 'anomalia' mantiene una certa ambiguità; infatti, esso significa non soltanto in generale 'non uniformità', ma anche quella particolare non uniformità apparente che è spiegata mediante l'epiciclo, anche dopo che, in base a questa spiegazione, è divenuta soltanto apparente, e 'anomalistico' è inteso qui in questa seconda accezione.
Il primo passo consiste nello stabilire la durata dei due periodi. Nel caso del Sole (III, 1) essi coincidono nell''anno tropico' (vale a dire il periodo in cui il Sole ritorna alla longitudine dell'equinozio di primavera, da distinguere dall''anno sidereo', cioè il periodo in cui il Sole ritorna nello stesso punto dello sfondo stellare; la differenza tra i due periodi è dovuta alla precessione degli equinozi). Quanto alla Luna, non soltanto questa coincidenza viene meno, ma le durate di tali periodi appaiono variare; dopo un'accurata analisi delle condizioni che devono essere soddisfatte per il loro corretto stabilimento, Tolomeo presenta i valori non soltanto per i periodi tropico e anomalistico, ma anche per quello cosiddetto 'sinodico' (ritorno della Luna nella stessa posizione rispetto al Sole), che gli servirà per i calcoli successivi (IV, 2-3).
Infine, è compiuta la stessa operazione per i pianeti, stabilendo insieme una relazione con il moto del Sole. Nel caso dei pianeti 'esterni' (Marte, Giove, Saturno) vale la relazione Y=L+A, dove Y sta per gli anni, L per i ritorni in longitudine e A per i ritorni in anomalia; nel caso di Saturno, per esempio, ogni 59 anni si danno 2 ritorni in longitudine più 57 ritorni in anomalia. Riguardo ai pianeti 'interni' (Mercurio e Venere) il moto medio in longitudine coincide con quello del Sole, dunque si ha Y=L, ed è dato il numero dei ritorni in anomalia ogni tanti anni; per esempio, nel caso di Venere si hanno 5 ritorni ogni 8 anni (IX, 3). Nel dare i valori di queste periodicità Tolomeo dipende da Ipparco ‒ anche se lo migliora sistematicamente ‒ e di conseguenza dalle più antiche ricerche astronomiche babilonesi, cui Ipparco si era rifatto, come oggi sappiamo; Tolomeo, però, non sembra più riconoscere chiaramente la provenienza originaria dei suoi dati iniziali.
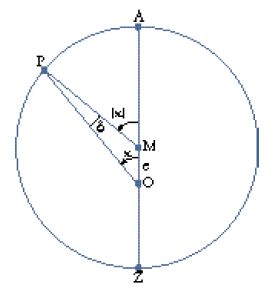
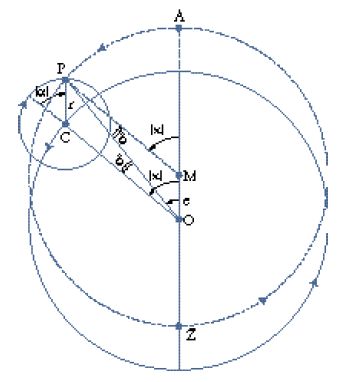
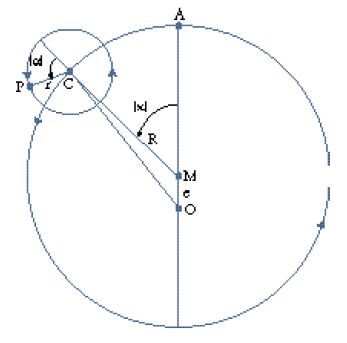
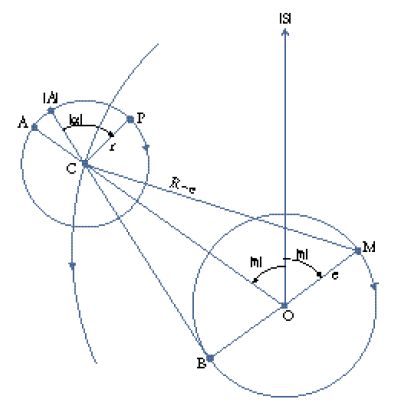
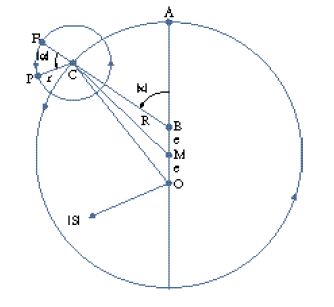
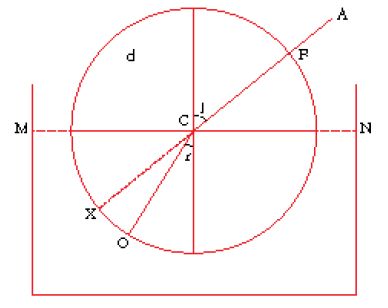
Il secondo passo consiste nel produrre, sulla base delle durate così stabilite, le tavole dei moti medi per i diversi periodi; in altre parole, sono date, per intervalli molto fitti, le posizioni che gli astri occuperebbero se ruotassero, per ciascun periodo, con un moto uniforme indipendente. Il significato del secondo passo si comprende appieno in base al terzo, la produzione dei modelli geometrico-cinematici. Il problema centrale dei moti dei pianeti era dato dalle loro variazioni di velocità; l'osservazione mostra come in tempi uguali essi percorrano archi disuguali dell'eclittica. L'astronomia matematica greca aveva pensato tali variazioni come anomalie apparenti, prodotte dalla composizione di più moti, ciascuno dei quali rispettava i requisiti di essere circolare e uniforme; si trattava di 'salvare i fenomeni' che apparivano caratterizzati da tali anomalie, producendoli a partire da quel tipo di composizioni. Dopo un primo tentativo in questo senso dovuto a Eudosso (attivo nella prima metà del IV sec. a.C.), con le cosiddette 'sfere omocentriche', famose per essere state incorporate nella cosmologia aristotelica ma presto abbandonate dagli astronomi poiché nella loro funzione di modelli presentavano difetti incorreggibili, nel III sec. a.C. era stata proposta la famiglia dei modelli cosiddetti degli eccentrici, dei deferenti e degli epicicli; con 'eccentrico' s'intende un cerchio che porta sulla sua circonferenza il pianeta (P nella fig. 3) e il centro M del quale non coincide con il centro O della Terra, mentre con 'deferente' s'intende un cerchio che ruota e sulla cui circonferenza si trova il centro C (fig. 4) di un altro cerchio più piccolo, l''epiciclo', il quale a sua volta ruota e porta il pianeta, P. Anche in questa seconda modellizzazione era mantenuto il doppio requisito della circolarità e dell'uniformità dei moti, del quale Tolomeo riaffermerà ripetutamente la validità. Alcune proprietà matematiche di questo tipo di modelli erano già state studiate da Apollonio di Perge (la cui acme si situa attorno al 200 a.C.), in un'ottica probabilmente più da matematico che da astronomo osservativo, e le prime applicazioni erano già state compiute da Ipparco. Adottando questi modelli Tolomeo non era dunque originale, ma si rifaceva a una tradizione già consolidata; sotto un certo profilo l'Almagesto è dunque il compimento del programma di Ipparco. Tolomeo non discute preliminarmente in generale le proprietà e le risorse della famiglia dei suoi modelli, ma le fa emergere progressivamente nel corso delle applicazioni a situazioni osservative via via più complesse. L'idea generale di questa modellizzazione consisteva nello spostare il centro di rotazione dei moti rispetto al punto di osservazione, la Terra; in tal modo un punto che si trovasse su un cerchio che ruota uniformemente attorno al proprio centro sarebbe stato visto ruotare non uniformemente dall'osservatore terrestre, mantenendo d'altronde una periodicità nelle sue variazioni di velocità. Nelle figure che seguono il piano del foglio rappresenta il piano dell'eclittica, O sta per il punto dell'osservatore, M per il centro dell'eccentrico, C per il centro dell'epiciclo, P per il pianeta (termine inteso nel suo significato etimologico di '[stella] errante' e quindi includente anche il Sole e la Luna), A per l'apogeo, Z per il perigeo, E per l'equante (v. oltre); le lettere greche indicano angoli variabili; l'inclusione in parentesi angolari (⟨ ⟩) indica che si fa riferimento a valori, posizioni e moti medi; R sta per il raggio del deferente, r per quello dell'epiciclo, e per l'eccentricità. Tolomeo presenta inizialmente i suoi modelli per il Sole, dunque per il caso più semplice, visto che per il Sole (e soltanto per esso) i periodi dei due ritorni fondamentali coincidono. Le variazioni di velocità interne al periodo solare sono manifestate immediatamente dall'ineguaglianza delle stagioni, cioè dai tempi disuguali in cui esso percorre i quattro quadranti in cui è divisa l'eclittica. Tolomeo espone anzitutto il cosiddetto 'modello a eccentrico' che è specifico per il Sole (fig. 3); se il Sole (P) si muove uniformemente su un cerchio di centro M (dunque un cerchio eccentrico rispetto alla Terra e alla sfera delle stelle fisse, al cui centro si trova la Terra), il suo moto apparirà variare a un osservatore in O sulla Terra (avrà la minima velocità all'apogeo e la massima al perigeo). Tolomeo passa poi a presentare il modello a deferente ed epiciclo, che s'adatta ai pianeti veri e propri (fig. 4; s'ignorino per il momento le linee tratteggiate, che riproducono per il pianeta P la situazione 'a eccentrico' della fig. 3). Qui, su un cerchio con centro O (il deferente dell'astro P) ruota uniformemente il punto C; a sua volta C è il centro di un cerchio (l'epiciclo di P) su cui ruota uniformemente in senso opposto P. Egli infine dimostra che i due modelli sono equivalenti, cioè producono per P lo stesso moto apparente (come si vede facilmente nella fig. 4, considerata in tutti i suoi elementi), se il raggio dell'epiciclo CP (nel secondo modello) è uguale all'eccentricità OM (nel primo modello), se il raggio OC del deferente è uguale al raggio MP dell'eccentrico e se P e C ruotano con la stessa velocità angolare attorno al proprio centro, in modo che gli angoli ⟨ϰ⟩ e ⟨α⟩ nei due modelli siano uguali e in tal modo i lati del quadrilatero OCPM restino sempre a due a due paralleli; la linea OP, che va dall'osservatore all'astro, sarà la stessa nei due casi (III, 3).
La corrispondente sezione sulla Luna affronta un caso un poco più complesso, dato che, come si è detto, i due periodi fondamentali non coincidono più. Tolomeo mostra anzitutto come in questo caso valga il modello epiciclico, a condizione che (cfr. fig. 4) le velocità di rotazione del cerchio del deferente e dell'epiciclo siano differenti (quindi siano differenti ⟨ϰ⟩ e ⟨α⟩), e dimostra immediatamente come valga anche in questo caso l'equivalenza con il modello con l'eccentrico, a condizione che i lati del quadrilatero OCPM, oltre a essere uguali, restino sempre paralleli; ciò richiede che, nel caso dell'eccentrico, il centro M (e quindi la linea degli absidi, ZA) ruoti a una velocità angolare uguale alla differenza delle velocità angolari di OC e CP nel caso del modello epiciclico. In tal modo è prodotto il modello iniziale (destinato a essere complicato) per la Luna (IV, 5). In base al modello epiciclico elaborato per la Luna si comprende nel modo migliore il significato delle tavole dei moti medi. La colonna dei moti medi in longitudine dà le posizioni di C, il centro dell'epiciclo, per qualsiasi momento (nell'ipotesi, ovviamente, che il deferente ruoti a velocità uniforme); la colonna dei moti medi in anomalia dà il moto angolare di P rispetto al proprio centro, C; infatti, il ritorno alla stessa velocità dell'astro visto dalla Terra coincide con il riprodursi della stessa configurazione deferente-epiciclo (per es., con il ritorno dell'astro all'apogeo) e, quindi, con il compimento di un intero giro dell'epiciclo.
Il caso dei cinque pianeti è più complicato, dato che essi presentano il fenomeno delle 'retrogradazioni', vale a dire che a intervalli non perfettamente regolari essi per un breve periodo invertono il verso del loro moto sulla volta celeste rispetto al verso del moto medio (dunque 'retrogradano', cioè 'vanno all'indietro') e poi ritornano a muoversi nel verso del moto medio. La spiegazione di questo fenomeno in base al modello epiciclico risale certamente al III sec. a.C., l'epiciclo essendo fatto ruotare nello stesso verso del deferente; in questa ipotesi il pianeta P, visto da O, appariva muoversi in verso opposto a quello medio (e dovuto al moto del deferente) allorché transitava al perigeo, a condizione che la velocità angolare dell'epiciclo relativamente a quella del deferente fosse sufficiente (si consideri la fig. 4, ignorando le linee tratteggiate e invertendo il verso di rotazione dell'epiciclo).
La capacità esplicativa del modello a epiciclo riguardo al fenomeno delle retrogradazioni dovette sempre apparire come la prova della validità di questa famiglia di modelli. In realtà, le cose presentavano una complicazione. Se le retrogradazioni si fossero ripetute regolarmente per i pianeti sarebbe stato sufficiente un modello epiciclico semplice (quale quello della fig. 4, ovviamente con il verso di rotazione dell'epiciclo invertito); l'osservazione mostra però una certa irregolarità sia negli archi sia nei tempi delle retrogradazioni. L'epiciclo spiegava le retrogradazioni, ma non questa variazione nelle retrogradazioni. Questa seconda anomalia fu spiegata mediante l'introduzione di un'eccentricità per il deferente. Il modello iniziale per i moti dei pianeti dovette perciò essere quello della fig. 5; si vede immediatamente che se O (l'osservatore) e M (il centro del deferente), non coincidono, le retrogradazioni appariranno variare per l'osservatore in O, in funzione del variare dell'angolo OM̂C.
Nella sezione sui pianeti in effetti Tolomeo inizia il terzo passo esponendo per essi il modello della fig. 5, ma quasi immediatamente egli v'introduce la complicazione che caratterizzerà il suo modello finale, cioè l''equante' (v. oltre), senza dare conto delle considerazioni che lo hanno portato a tale complicazione (IX, 5). In questo punto dunque viene meno il parallelismo tra la sezione sulla Luna e quella sui pianeti, che altrove è sempre mantenuto; mentre per la Luna i passi che portano dal modello iniziale a quello finale sono esposti e dunque sono visibili, per i pianeti non lo sono e Tolomeo produce le derivazioni dei valori numerici per i parametri dei pianeti immediatamente per i modelli finali. Perciò conviene separare per un tratto l'esposizione della sezione sul Sole e sulla Luna da quella sui cinque pianeti.
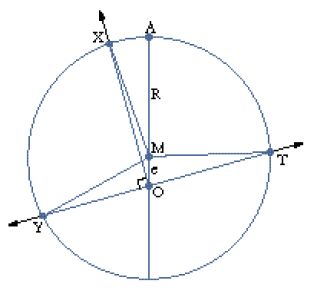
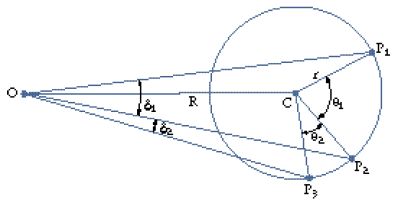
Il quarto passo consiste nella derivazione di quei parametri, in base ai quali i modelli acquisiscono la capacità di prevedere, ossia di calcolare le posizioni vere dell'astro per qualsiasi momento. Per il Sole, si tratta essenzialmente di determinare l'angolo δ (fig. 3) ‒ la 'prostaferesi' (prosthaphaíresis), all'incirca la 'somma-sottrazione' ‒ in funzione dell'angolo ⟨ϰ⟩; allora l'angolo ϰ, che dà la posizione vera del Sole, sarà calcolabile sommando o sottraendo δ da ⟨ϰ⟩, a seconda che il Sole si trovi dall'una o dall'altra parte della linea AZ. Ma ⟨ϰ⟩ è in generale un angolo con vertice in M, il centro del moto uniforme, dunque è noto in base ai moti medi del Sole; si tratta allora, per determinare δ in funzione di ⟨ϰ⟩, di calcolare il rapporto tra il raggio MP e l'eccentricità OM. Tolomeo considera le tre posizioni del Sole ai due equinozi e a un solstizio; ottiene così (fig. 6) due coppie di angoli, la prima con vertice in O (XÔY e TÔX, dove entrambi sono noti, essendo retti), la seconda coppia, cioè TM̂X e XM̂Y, con vertice in M (dove di nuovo entrambi sono noti, in base ai moti medi del Sole, essendo nota la durata delle stagioni). Diventa così possibile calcolare trigonometricamente il rapporto tra MP e OM (cfr. la fig. 6 con la fig. 3), quindi determinare δ in funzione di ⟨ϰ⟩. Il modello consente quindi di calcolare ϰ per qualunque momento (III, 4-5). Per la Luna, in una situazione più difficile, si tratta fondamentalmente di determinare il rapporto tra il raggio del deferente, OC, e quello dell'epiciclo, CP. Qui Tolomeo parte da tre eclissi lunari; essendo noti gli intervalli di tempo, sono calcolabili i moti medi sia in longitudine sia in anomalia fra i tre punti. Le tre configurazioni deferente-epiciclo nelle tre eclissi sono allora giustapponibili in una sola, quale quella della fig. 7, nella quale sono noti sia gli angoli δ₁ e δ₂, sia gli angoli θ₁ e θ₂. Il lettore immagini due configurazioni distinte deferente-epiciclo e compia mentalmente l'operazione di tenere ferma l'una e di ruotare l'altra, in modo che i due centri del deferente coincidano; allora l'angolo δ sarà dato dalla differenza tra il moto in longitudine medio e quello vero per l'intervallo di tempo considerato; ripeta poi la stessa operazione per la terza configurazione. Quanto agli angoli θ, essi sono noti, per l'intervallo di tempo considerato, in base al moto medio in anomalia. Il problema a questo punto è ridotto a quello di calcolare il rapporto tra OC e CP, dati quei quattro angoli; in base a un'analisi molto brillante, esso è risolto trigonometricamente (IV, 6).
Questo metodo di calcolo per la Luna risaliva già a Ipparco e ne va segnalata l'importanza, oltre che l'ingegnosità; l'ideazione di procedimenti come questo marca la differenza tra la prima fase dell'astronomia antica e la seconda. Mentre nella prima, caratteristicamente con Eudosso, ai modelli geometrico-cinematici si richiedeva di generare moti somiglianti a quelli osservati, lo sforzo di dotare i modelli dei valori numerici per alcuni loro parametri è associato allo sforzo di renderli capaci di produrre previsioni e in questo modo di essere precisati. La svolta in questo senso va attribuita a Ipparco. Si aggiunga che in tutta la parte dell'Almagesto fin qui delineata Tolomeo ha una forte dipendenza da Ipparco, anche se si cura costantemente di raffinarne i procedimenti e di precisarne i risultati, e se sono molto probabilmente sue le tavole dei moti medi. Da qui in avanti, ciò che esporremo sarà frutto quasi esclusivo della ricerca di Tolomeo.
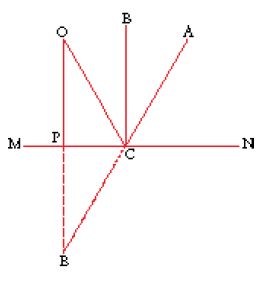
Il quinto passo consiste nei controlli e nell'introduzione di complicazioni. Per il Sole esso è del tutto assente, perché il modello iniziale è già soddisfacente. Non così per la Luna: mentre nelle opposizioni con il Sole (cioè nelle situazioni di possibili eclissi lunari) e nelle congiunzioni l'accordo con le osservazioni è buono, Tolomeo rileva anzitutto una discrepanza con le osservazioni alle quadrature (cioè a 90° di distanza dal Sole): l'angolo di prostaferesi vi appare più grande di quanto i calcoli basati sul suo modello consentano. Questa situazione è fronteggiata introducendo nel modello una sorta di meccanismo a manovella, che avvicina l'epiciclo alle quadrature, di modo che appaia più grande (V, 2; fig. 8). Il centro C dell'epiciclo ruota intorno a M, il quale a sua volta ruota uniformemente intorno alla Terra, O, in modo tale che l'angolo ⟨S⟩ÔM (≡⟨η⟩) sia sempre uguale all'angolo ⟨S⟩ÔC. Dato che ⟨S⟩ rappresenta il Sole medio, è chiaro che questo modello è identico al precedente nelle congiunzioni e nelle opposizioni, mentre nelle quadrature si ha il massimo avvicinamento dell'epiciclo ad O, quindi il massimo incremento dell'anomalia; in base a osservazioni è poi calcolata la lunghezza relativa di OM. Tolomeo ripete i controlli per il modello così complicato e, trovando una discrepanza residua con le osservazioni agli ottanti (cioè a 45° e 135° di distanza dal Sole), fronteggia questa situazione con un'ultima e finale complicazione (V, 5), consistente nel contare l'anomalia, ⟨α⟩, non a partire da A, ma da ⟨A⟩ (in modo che ⟨A⟩C sia diretto verso il punto B, collocato in opposizione a M sul cerchio su cui è M).
Questo modello finale rende bene i moti in longitudine della Luna. Merita tuttavia due osservazioni. In primo luogo, la distanza della Luna dalla Terra varia da un massimo, R+r, a un minimo, R−2e−r; in base ai calcoli tolemaici, da un massimo di circa 65 (per R=60) a un minimo di circa 34. Ne segue che il massimo diametro apparente della Luna dovrebbe essere all'incirca il doppio di quello minimo, mentre la variazione che si osserva è molto minore (è la più vistosa discrepanza dell'Almagesto con i fenomeni). Non sembra possibile che Tolomeo ignorasse questo, e tuttavia non dice nulla in proposito. In secondo luogo, nel modello finale il centro C dell'epiciclo, dato che ruota uniformemente attorno a O, ruota non uniformemente attorno al proprio centro M. Si tratta qui non di una discrepanza con i fenomeni, ma di una deroga (la prima) al principio dell'uniformità dei moti circolari celesti; anche in questo caso Tolomeo non fa nessuna menzione in proposito.
Un'analoga deroga a tale principio è presente in tutti i modelli dei cinque pianeti; qui Tolomeo non soltanto non la commenta, ma neanche lascia vedere il percorso d'indagine in base al quale la introduce. Si è già mostrato (fig. 5) il modello da cui egli deve essere partito e sembra indubbio che ci sia stata un'elaborazione di tale primo modello analoga a quella compiuta per la Luna. In ogni caso, il modello finale per i tre pianeti esterni è quello rappresentato nella fig. 9. Il pianeta, P, ruota attorno al centro dell'epiciclo, C, il quale ruota attorno al centro M, eccentrico rispetto a O, la Terra. C ruota però uniformemente se visto da E, l'equante, un punto opposto a O rispetto a M ed equidistante da M (dunque C ruota non uniformemente attorno al proprio centro, M); il moto in anomalia è contato da F; il raggio r=CP dell'epiciclo è sempre parallelo alla freccia O⟨S⟩ che punta verso il Sole medio; in tal modo è rispettata la relazione Y=L+A, esposta nel primo passo. Per i due pianeti interni vale invece, come si è detto, la relazione Y=L e la longitudine del centro dell'epiciclo, C, coincide con quella del Sole medio (mentre il loro epiciclo ruota 'liberamente'). Perciò nel modello di entrambi la freccia O⟨S⟩ va eliminata. Il modello per Mercurio, il pianeta più difficile, contiene un'ulteriore complicazione, dovuta all'esigenza di far variare l'eccentricità; essa è ottenuta, come nel caso della Luna, mediante un meccanismo a manovella, che fa ruotare il centro del deferente. I parametri da determinare sono qui essenzialmente le lunghezze dell'eccentricità, e=OM, e del raggio dell'epiciclo, r=CP, relativamente a quella del raggio del deferente, R=MC. Nel caso dei pianeti interni la situazione è più facile, perché, da una parte, la loro distanza angolare dal Sole, l'elongazione, è direttamente osservabile, e perciò è immediatamente data l'ampiezza massima dell'epiciclo, e, dall'altra parte, la linea OMEA si ricava da configurazioni simmetriche; diviene allora relativamente semplice calcolare trigonometricamente sia l'eccentricità sia il raggio dell'epiciclo a partire dalle variazioni osservabili dell'angolo CO‸P quando l'elongazione è massima (IX, 6-7; X, 1-2). Per i pianeti esterni la situazione è più difficile, dato che tali osservazioni dirette non sono più possibili. Tolomeo affronta questa difficoltà anzitutto scegliendo tre osservazioni nelle quali fosse azzerata l'anomalia prodotta dall'epiciclo, cioè tre opposizioni (dato che, per il parallelismo di CP con la direzione del Sole medio, il pianeta in opposizione è allineato con il centro dell'epiciclo, C). A questo punto il problema è affine a quello già visto per la Luna, ossia trovare il rapporto tra OM e MC dati due angoli con vertice in O e due con vertice in M i cui lati passano per gli stessi punti della circonferenza (il fatto che O in questo caso sia interno al cerchio con l'altro centro, mentre nel caso precedente era esterno, non comporta una diversità essenziale nel procedimento, come Tolomeo sa, e forse fu il primo a comprendere). Qui però c'è la difficoltà ulteriore, costituita dalla separazione del centro del deferente dall'equante; Tolomeo l'affronta mediante un ingegnoso procedimento iterativo. Precisamente, opera inizialmente come se i centri del deferente e dell'equante coincidessero, ottenendo così una prima approssimazione; su questa base calcola una seconda migliore approssimazione; ripete poi il procedimento quanto in ciascun caso ritiene necessario (X, 6-7; XI, 1; XI, 5). Quasi certamente si tratta di un metodo da lui ideato. Una volta stabilito il rapporto tra OM e MC, diviene possibile calcolare la lunghezza relativa del raggio dell'epiciclo sulla base di altre osservazioni; così risultano determinati i parametri del modello finale necessari per il calcolo delle longitudini.
Il sesto e penultimo passo consiste nella produzione delle tavole delle correzioni, in base alle quali calcolare la posizione longitudinale vera del pianeta per qualsiasi momento di tempo. L'idea generale è facilmente comprensibile in riferimento ai modelli semplici deferente-epiciclo del Sole e della Luna. Mediante le tavole dei moti medi si calcola, a partire da una posizione stabilita per l'astro in un momento iniziale ‒ l''epoca'‒ la posizione di C; si ottiene così l'angolo ⟨ϰ⟩ (qui uguale a ⟨α⟩); a questo punto l'angolo δ, da sottrarre o sommare a ⟨ϰ⟩, è determinato in funzione di ⟨ϰ⟩, visto che si conoscono le lunghezze relative dei raggi del deferente e dell'epiciclo. Le tavole delle correzioni per questo caso più semplice contengono appunto i valori di δ in funzione di ⟨ϰ⟩ (III, 6). Le tavole del modello finale della Luna sono più complicate, perché δ varia anche in funzione di una seconda variabile, l'angolo 2⟨η⟩, dal quale dipende il variare della distanza dell'epiciclo. Semplificando, Tolomeo aggiunge alle colonne che danno i valori della correzione richiesta dal modello semplice altre colonne, che danno, in funzione di 2⟨η⟩, i valori della correzione da apportare alla prima correzione, ottenendo così l'angolo di prostaferesi e quindi la posizione vera in base al modello finale (V, 8). Ancora più complicate, ma fondamentalmente analoghe, sono le tavole delle correzioni per i cinque pianeti (XI, 11). Infine, il settimo e ultimo passo consiste nelle istruzioni per l'uso delle tavole (per il Sole, III, 8; per la Luna, V, 9; per i pianeti, XI, 12). In alcuni punti la procedura tolemaica conterrebbe alcuni calcoli laboriosi e complicati. Qui tuttavia egli introduce, in base alle tavole, alcune procedure di interpolazione, che consentono un calcolo della correzione abbastanza facile, consistente in una sequenza di somme e sottrazioni.
Così, dunque, la teoria dei moti in longitudine è giunta a compimento. Prendendo le mosse da osservazioni che risalgono anche a tempi antichi relative alle periodicità principali, e spiegando ciascuna di esse in base a moti circolari e uniformi distinti, sono state prodotte anzitutto le tavole dei moti medi, quindi i modelli iniziali, in base alle diverse caratteristiche dei moti osservabili dei diversi astri; poi tali modelli sono stati analizzati geometricamente e mediante le risorse della trigonometria ne sono stati determinati i parametri che li rendevano capaci di previsioni. Essendo emerse discrepanze con le osservazioni, tali modelli sono stati resi più complicati, in tutti i casi separando il centro del deferente dal centro del moto uniforme, e quindi introducendo moti non uniformi (ma sempre periodici), dove lo scostamento dall'uniformità resta sempre determinato in riferimento a un moto uniforme. Così sono stati calcolati i parametri finali, e si sono potute produrre le tavole delle correzioni, in funzione di due variabili, in modo da passare dai moti medi alle posizioni vere, cioè quelle che si osservano. L'Almagesto è perfettibile, sia nel senso che la ripetizione delle osservazioni a grandi distanze di tempo ne potrà ridurre le imprecisioni, sia nel senso che i modelli planetari potranno subire modificazioni (una di queste modificazioni sarà apportata dallo stesso Tolomeo; infatti, nelle Ipotesi planetarie i modelli dell'Almagesto per i moti in latitudine ‒ i modelli più complicati dell'astronomia tolemaica, che in questa sede non abbiamo trattato ‒ sono leggermente ritoccati e semplificati). Sembra peraltro essere definitivo, agli occhi di Tolomeo, l'impianto fondamentale della teoria, il cui successo ha un significato che va al di là della scienza in senso stretto, visto che trova l'ordine appropriato alla natura delle cose divine.
Il destinatario elettivo dell'Almagesto è riconoscibile mediante un confronto con le Tavole manuali, un'opera in cui Tolomeo, dopo un riassunto molto breve della sua teoria, riproduce con qualche modificazione secondaria le tavole della sua opera maggiore. Il lettore delle Tavole manuali è messo in grado di calcolare le posizioni vere, anche senza una effettiva comprensione delle dimostrazioni che sono state alla base della produzione delle tavole. Si tratta dunque di un fruitore 'basso' della scienza tolemaica, il quale, secondo il modello antico, non è in senso proprio uno scienziato. Il destinatario dell'Almagesto di contro è un fruitore 'alto', che comprende tutti i passi e le dimostrazioni; l'attenzione didattica di Tolomeo è rivolta a questo lettore, come emerge in particolare da un passo dell'opera.
Nella produzione delle tavole per la correzione dei moti in longitudine dei cinque pianeti, la terza colonna contiene i valori che si darebbero per il modello più semplice, quello in cui il centro del deferente e il punto equante non sono ancora separati, ma coincidono; la quarta poi dà la correzione da apportare alla terza, a seguito di tale separazione. Tolomeo osserva che, per l'uso che se ne fa nei calcoli, basterebbe una sola colonna, che combinasse (mediante una somma) i valori di queste due; e in effetti nelle tabulazioni delle Tavole manuali le due colonne sono fuse in una sola. Ma, dice, "in questa sede, in quanto questa è una sýntaxis, è appropriato mettere in vista siffatto modo di separare relativo all'anomalia zodiacale [cioè, quella spiegata mediante l'eccentrico] e perciò tabulare in due colonne" (XI, 10). I passi compiuti vanno dunque lasciati in vista, perché ciò è didatticamente utile per un lettore in grado di comprendere a fondo l'impianto dell'opera e le dimostrazioni contenute, qual è il lettore di una sýntaxis. Questo termine, il cui senso corrente è 'composizione, trattazione complessiva', acquisisce in questo passo la connotazione di 'trattazione scientifica'; il significato del titolo originale dell'opera, Mathēmatikḕ sýntaxis, può dunque essere parafrasato come 'trattazione scientifica, cioè basata su dimostrazioni geometriche, dell'ambito privilegiato dell'applicazione delle matematiche, ossia dell'ambito astronomico'.
Le 'Ipotesi planetarie'
Seconda in importanza tra le opere astronomiche tolemaiche è Ipotesi planetarie (in due libri, di cui la prima parte del Libro I nell'originale greco e tutto il resto in traduzione araba), successiva all'Almagesto. L'intento inizialmente dichiarato è quello d'istruire alla costruzione di un corretto modello meccanico dei moti planetari (cioè un planetario). Tolomeo vi espone succintamente i modelli della sua opera maggiore (con alcuni miglioramenti secondari), andando però oltre sotto due profili.
Le distanze assolute dei cinque pianeti non erano trattate nell'Almagesto; come si è detto, le lunghezze dei vari raggi erano determinate in rapporto a quella del raggio del deferente, alla quale era assegnato in tutti i casi il valore convenzionale 60. Soltanto per la Luna e per il Sole si era potuto calcolare le distanze assolute, perché per la Luna è discernibile la parallasse (cioè la differenza tra la posizione 'vera' e la posizione apparente del corpo celeste derivante dal fatto che l'osservatore non si trova al centro della Terra, bensì alla distanza di un raggio terrestre), e Tolomeo disponeva di un metodo, già elaborato da Ipparco, per ricavare la distanza del Sole da quella della Luna. Il risultato dei suoi calcoli era stato (V, 15) per la Luna una distanza media di 59 raggi terrestri (vicina al vero), per il Sole una distanza media di 1210 raggi terrestri (20 volte inferiore al vero; con il metodo di Tolomeo un piccolo errore nella misurazione del diametro solare produceva un grande errore nel risultato finale).
In base all'Almagesto, dunque, qualsiasi ordine ascendente per i cinque pianeti era arbitrario, visto che per essi la parallasse non è osservabile; Tolomeo aveva adottato il tradizionale ordine Mercurio, Venere, Marte, Giove, Saturno, ossia quell'ordine che, per gli ultimi tre, associava la diminuzione della velocità angolare del moto in longitudine con la maggiore distanza da noi (i pianeti più lontani erano quelli che compivano nel tempo maggiore un giro attorno a noi). Questa associazione, che Tolomeo accetta, lascia però aperto qualsiasi ordine per ciò che concerne Mercurio, Venere e il Sole, che hanno lo stesso moto medio in longitudine. Affrontando questo problema nelle Ipotesi planetarie, egli ipotizza che la distanza massima di ciascun pianeta coincida con la distanza minima del pianeta successivo; allora, dato che la Luna (di cui sono note le distanze assolute) è certamente l'astro più vicino a noi, le distanze assolute dei cinque pianeti diventano calcolabili qualora se ne conosca il corretto ordine ascendente; si trova che, se si mettono dopo la Luna Mercurio e Venere in quest'ordine, la distanza massima di Venere coincide quasi perfettamente con quella minima del Sole e quindi lo spazio tra la Luna e il Sole in questa ipotesi risulta perfettamente riempito. Questa straordinaria coincidenza, derivante da una misurazione sbagliata, dovette apparire a Tolomeo come una conferma non soltanto della collocazione del Sole tra Venere e Marte, ma anche in generale della bontà del suo sistema; egli prosegue determinando nello stesso modo tutte le distanze assolute, fino a quella della sfera delle stelle fisse (Goldstein 1967, pp. 6-8). A questo punto Tolomeo aveva, come base fisica per la sua astronomia, un Universo costituito da sfere concentriche prive di vuoti tra loro e nel cui spessore si muovevano i pianeti, nel modo ricostruibile in base ai modelli dell'Almagesto. Questo Universo acquisiva così tratti che lo rendevano razionalmente soddisfacente, un kósmos nel senso greco del termine, in particolare platonico ed aristotelico; "è impensabile ‒ dice una volta ‒ che ci sia in Natura un vuoto, o qualsiasi cosa priva di significato e utilità".
Di questo Universo così caratterizzato Tolomeo, nel Libro II delle Ipotesi planetarie, si chiede quali forme abbiano i corpi fisici, cui i cerchi dei modelli appartengono. Si tratta di una questione fisica, ma il fisico dipende qui in certa misura dal matematico (cioè dall'Almagesto), da cui ricava quali siano le forme corporee ammissibili, cioè quelle combinando le quali si possono generare i moti fenomenici degli astri. Da un punto di vista matematico (II, 4) due sono le articolazioni corporee possibili per il cielo. La prima ‒ immediatamente suggerita dal Libro I ‒ è che sia articolato in sfere, cosicché per ciascun pianeta ci sarebbe una grande sfera di un certo spessore, la quale compirebbe il moto medio in longitudine e nello spessore della quale sarebbe portata una sferetta, che percorrerebbe il moto in anomalia e porterebbe su un suo cerchio massimo il pianeta. La seconda articolazione è basata su segmenti di sfere, ottenuti tagliando le sfere dei pianeti poco sopra e poco sotto il piano dell'eclittica, in modo che per ciascun pianeta ci sarebbe un grande anello, il cerchio deferente, il quale compirebbe il moto medio in longitudine e all'interno del quale ci sarebbe una sorta di tamburello, l'epiciclo, il quale compirebbe il moto in anomalia e porterebbe sulla sua circonferenza il pianeta. Questa seconda articolazione si può intuire meglio se si pensa che i suoi anelli e tamburelli corrispondono all'incirca ai cerchi della parte esposta alla vista di un planetario, dove il piano comune dei loro diametri corrisponderebbe all'incirca al piano dell'eclittica, mentre i ruotismi che generano i loro moti sarebbero collocati dietro.
Tolomeo argomenta a lungo a favore della seconda alternativa (II, 5-8); il senso d'insieme delle sue argomentazioni è molto caratteristico. Se si opta per la prima alternativa, è perché, a fronte della complessità dei moti visibili e della loro scomposizione in più moti semplici, si pensa che, in corrispondenza con ciascuna componente del modello con cui si ricostruisce la complessità dei moti, ci sia un corpo distinto e separato, il quale è sorgente e origine del solo proprio moto semplice. La complessità dei moti visibili è ottenuta mediante vincoli meccanici, quali i perni, ma allora devono esserci le sfere complete, perché altrimenti non si saprebbe dove collocare i perni. Merita di essere segnalato che Tolomeo pone una considerazione di questo tipo alla base dell'introduzione delle sfere celesti nella Metafisica di Aristotele. Questo ragionamento non vale però se si pensa l'astro come la fons et origo di tutta la complessità dei moti che compie, e se si considera l'articolazione tamburello-anello come il corpo proprio dell'astro, nel senso che al suo interno (e soltanto al suo interno) si trasmette, a partire dall'astro, la forza vitale interna, che lo fa muovere così come si muove. Passando dall'astro al tamburello e poi all'anello la forza vitale si differenzia in modo proporzionato e regolato, in analogia ‒ dice Tolomeo ‒ con la trasmissione della forza vitale entro l'articolazione corporea di un animale, dove nelle diverse parti si ha una diversificazione proporzionata della forza erogata, con la conseguente produzione di moti complessi, visto che tutte le diverse parti concorrono al moto d'insieme.
Questa discussione occupa lo spazio che per noi è occupato dalla dinamica celeste (del tutto mancante in Tolomeo). È da notare come Tolomeo scelga tra le due alternative quella in base alla quale ci sono corpi soltanto per una parte dei componenti dei modelli dell'Almagesto; così, per esempio, nel caso della Luna c'è una base corporea per l'epiciclo e il cerchio del deferente, ma non per il 'meccanismo a manovella' del modello finale (base del resto impossibile perché dovrebbe trovarsi nella sfera sublunare). Va sottolineato, inoltre, che l'anello corporeo entro cui si diffonde la forza vitale erogata dall'astro si muove ruotando su sé stesso, senza trovare alcun ostacolo né alcuna resistenza al suo esterno; dunque questa concezione non soltanto non ha una dinamica celeste, ma la esclude. Tolomeo opta per l'ammissione di una corporeità celeste specifica, l'etere aristotelico, il quale ha le proprietà richieste dalla sua concezione, dato che per l'assoluta sottigliezza e fluidità non offre nessuna resistenza ai moti che si compiono in esso ‒ moti dunque che in questo senso sono liberi, in quanto dipendono soltanto dalla volontà e dall'intelletto di ciò che li compie, e ciò che li compie sono dèi, i quali realizzano senza fatica la loro vita immortale. Si noti come in questa sezione Tolomeo da un lato si esprima negativamente sulle sfere celesti della Metafisica aristotelica, dall'altro lato adotti l'etere aristotelico.
Alla luce di una considerazione combinata dell'Almagesto e delle Ipotesi planetarie si può accennare a una questione storiografica di rilievo, quella relativa al modo in cui Tolomeo pensava i suoi modelli geometrico-cinematici dei moti planetari. Secondo una tesi classica di Pierre Duhem (condivisa da molti altri) agli occhi di Tolomeo tali modelli erano meri artifici, strumenti per calcolare le posizioni degli astri in base alle ipotesi più semplici; non avevano altra funzione oltre questa, e dunque non si poneva una questione di verità relativamente alle ipotesi; in particolare, non si risaliva dai modelli alla 'natura' di ciò che compie i moti celesti. Una tale concezione può essere classificata come 'strumentalista'; essa interpreta il celebre motto 'salvare i fenomeni' (più volte citato da Tolomeo) nel senso restrittivo per cui nell'indagine si tratta di produrre previsioni in accordo con le osservazioni, senza andare oltre.
Nella cultura dell'epoca, peraltro, non era presente nessuna formulazione netta della concezione strumentalista, neppure delle opposizioni che la definirebbero, e perciò, come è logico aspettarsi, nemmeno in Tolomeo sono leggibili nette prese di posizioni esplicite in proposito. La tesi di Duhem perciò va discussa facendo in buona misura ricorso all'implicito. Per ciò che concerne le Ipotesi planetarie tale tesi è palesemente falsa. È vero che Tolomeo sceglie, tra le due articolazioni della corporeità celeste compatibili con gli esiti dell'Almagesto, quella che gli consente di considerare non reali alcune parti dei suoi modelli, ma il punto è che pensa che ci sia da scegliere e sceglie, e dunque usa i modelli per uno scopo che va oltre quello riconosciuto ad essi da uno strumentalista, visto che se ne serve per produrre una descrizione della base fisica dei fenomeni celesti. Gli anelli e i tamburelli corrispondono a parti dei modelli, sono la base corporea dei cerchi deferenti e degli epicicli; non tutti gli aspetti dei modelli sono reali, in particolare non lo sono quelli necessari per tradurre i modelli in meccanismi, ma la sua 'dinamica' vitalistica è appunto intesa a fornire la spiegazione reale di come quegli anelli e quei tamburelli celesti compiano i moti ricostruiti dai modelli anche senza meccanismi.
Si potrebbe sostenere che l'approccio di Tolomeo è strumentalista nell'Almagesto, per poi diventare realista nelle Ipotesi planetarie, ma neppure questa posizione è sostenibile. Si è già accennato a come egli, nel discutere la questione se la Terra si muova o resti immobile, non si limitasse a considerare le varie ipotesi sotto il profilo della loro compatibilità con i fenomeni, ma andasse oltre, introducendo ragioni fisiche per confutare un'ipotesi geometricamente equivalente alla propria, ponendosi quindi la domanda circa la verità (e non la mera adeguatezza) delle ipotesi astronomiche. Inoltre, egli fronteggia una possibile obiezione generale, consistente nel rilevare come la complessità delle ipotesi, sulla cui base egli salva i fenomeni planetari, comporti per i corpi a essi sottesi difficoltà e impedimenti nel compimento dei moti (XIII, 2). La replica di Tolomeo non è quella di uno strumentalista; egli dice infatti che, data la natura eterea dei corpi celesti, non ci sono in cielo le difficoltà e gli ostacoli che si hanno nei movimenti terrestri, e aggiunge che la 'semplicità' per i moti dei corpi celesti, e divini, consiste nel loro compiersi costantemente senza sforzo ‒ semplicità dunque del tutto compatibile con la complessità dei modelli necessari per salvare i fenomeni. Come si vede, Tolomeo qui fa ricorso alle proprietà fisiche del corpo etereo e allude già a una dinamica vitalistica, in modo convergente con quanto dirà nelle Ipotesi planetarie.
Si è visto (v. sopra: par. 2) come il modello finale della Luna comporti una forte discrepanza tra la variazione calcolabile nel diametro apparente dell'astro e la variazione effettivamente osservabile, e come Tolomeo taccia su questa discrepanza. Tale silenzio potrebbe essere giustificato, se Tolomeo considerava il proprio modello lunare valido soltanto per il calcolo delle posizioni in longitudine, e non per le distanze. Questo indizio di un Tolomeo consapevolmente strumentalista è tuttavia illusorio ‒ qualunque sia la spiegazione di quel suo silenzio ‒ dato che in una sezione successiva (V, 13) egli si serve degli esiti del suo modello nella teoria della parallasse lunare e dunque nel calcolo delle distanze, considerando così le distanze ottenute in base al modello altrettanto reali quanto le posizioni.
Molti astronomi successivi, tra i quali Copernico, rimprovereranno a Tolomeo la sua deroga al principio dell'uniformità dei moti circolari nei suoi modelli, non soltanto con l'introduzione dell'equante per i pianeti, ma già per la Luna (v. sopra: par. 2). Il fatto che egli si sia sentito autorizzato a ciò potrebbe essere interpretato come un'ulteriore prova di un suo strumentalismo. Infatti ‒ si potrebbe sostenere ‒ se si tratta di salvare i fenomeni, cioè di calcolare posizioni, allora, se a questo scopo risulta conveniente lasciar cadere un principio quale quello dell'uniformità dei moti, lo si lascia cadere, perché un principio di questo tipo vale soltanto finché è utile per il calcolo; Tolomeo deve aver giustificato a sé stesso quell'abbandono in questo modo, cioè al modo di uno strumentalista. Ora, ciò si scontra con il fatto che Tolomeo si esprime sempre (anche in un passo in cui c'è certamente un'allusione all'equante, IX, 2) come se egli mantenesse l'uniformità dei moti. L'interpretazione strumentalistica dell'equante indurrebbe dunque a pensare o che Tolomeo sia qui in conflitto con sé stesso o che mascheri il suo pensiero. Questo non sembra necessario; tutti gli scostamenti dall'uniformità sono infatti ottenuti a partire da modelli che si attenevano al principio di uniformità e soprattutto restano regolati e misurati in riferimento a un moto uniforme. La fisica vitalistica rende possibile a Tolomeo interpretare quegli scostamenti come effetti della differenziazione proporzionata che la forza dell'astro subisce nel trasmettersi all'interno della sua articolazione corporea. Questa è una giustificazione possibile dell'introduzione dell'equante, che non ha un preciso sostegno nelle parole di Tolomeo, come del resto non l'ha neppure quella che ne fa uno strumentalista mascherato; vi si è fatto cenno per mostrare come l'interpretazione strumentalistica dell'equante non sia l'unica possibile, tanto più in presenza di una 'fisica' basata sul vitalismo e sull'etere, che sembra elaborata ad hoc per consentire a Tolomeo un uso dei suoi modelli che va oltre il calcolo.
Un'ultima considerazione merita di essere fatta. Le spiegazioni fisiche che Tolomeo suppone per i moti celesti sono tali da non comportare, si può dire, nessun vincolo; la forza vitale degli astri operante in una corporeità che non offre resistenza può sempre essere addotta a spiegazione di quei moti, purché essi rivelino una regolarità adeguata a enti divini. D'altra parte, egli stesso dichiara che le dimostrazioni che mettono in gioco la materia sono sempre congetturali e meno certe delle dimostrazioni matematiche (Almagesto, I, 1), tra le quali sono comprese certamente anche le costruzioni dei modelli. Questa concezione generale e la 'fluidità' della sua fisica convergono nel far sì che Tolomeo nel produrre i suoi modelli nell'Almagesto si mantenga sempre al riparo da considerazioni fisiche e insieme possa confidare di disporre di adeguate spiegazioni fisiche, per il momento ulteriore in cui si tratterà di proporle, facendo sì quindi che egli operi come se fosse uno strumentalista. Se si ha una concezione generale della scienza di tipo strumentalistico diventa legittimo rilevare come la parte più valida della scienza tolemaica sia quella in cui egli agisce come uno strumentalista, elaborando modelli per calcolare e prevedere posizioni osservabili. In ogni caso, tuttavia, non fu questo il modo in cui egli pensò la sua scienza, in un quadro culturale in cui, inoltre, non era presente nessuna posizione strumentalista chiaramente formulata.
L'astrologia e la geografia
Tolomeo redasse anche un trattato di astrologia in quattro libri, Tetrabiblos. L'astrologia, diffusasi progressivamente nell'area greca negli ultimi secoli dell'era pagana, era l'erede dell'antica tradizione divinatoria. La sua opera di drastica restrizione delle pratiche precedenti, visto che per essa era possibile conoscere in anticipo il corso degli eventi soltanto mediante gli astri, aveva al contempo il senso di un rafforzamento della pretesa di prevedere; le configurazioni celesti, essendo perfettamente note in anticipo in base all'astronomia, costituivano una base sicura per le previsioni se si ammetteva una correlazione tra esse e ciò che avviene sulla Terra. Tolomeo intese questa correlazione nel suo senso più forte, in quanto per lui le configurazioni celesti erano fonti fisiche di influenze, dunque erano cause degli eventi terrestri. Tale efficacia causale gli era esemplificata, conformemente alla tradizione, dall'evidente influenza del Sole e della Luna sulle condizioni ambientali e meteorologiche (I, 2); lo scritto sulle Fasi delle stelle fisse (in due libri, di cui ci è rimasto soltanto il secondo) produce sistematicamente informazioni sulle variazioni meteorologiche associate alle ricomparse delle stelle principali. Contro l'obiezione che le stelle erano troppo lontane per avere influenza sulla Terra la replica di Tolomeo fu, sostanzialmente, che non c'era nessun motivo per negare per le stelle ciò che si ammette come evidente per il Sole e la Luna (I, 2).
Contro l'argomento antiastrologico che faceva leva sui frequenti fallimenti della previsione basata sulle stelle, Tolomeo sviluppò un insieme di repliche distinte ma convergenti. Anzitutto ne alleggerì il peso, rilevando che non andavano imputati all'astrologia i fallimenti dei falsi astrologhi, cioè dei praticanti incompetenti, disonesti e millantatori. Soprattutto sottolineò poi che è la natura stessa dell'astrologia a rendere possibile i suoi errori, in primo luogo perché essa verte sulle qualità della materia e di conseguenza è congetturale e non sicura nelle sue previsioni, in secondo luogo perché essa inevitabilmente si basa su correlazioni imprecise tra configurazioni celesti ed eventi terrestri (il ritorno preciso delle stesse configurazioni richiede infatti un tempo che eccede di molto l'esperienza umana). Ciò non invalida però la possibilità della previsione astrologica, così come la previsione meteorologica (che è associata a cicli più brevi, ma in fondo procede nello stesso modo) non è invalidata dai suoi fallimenti (I, 2).
Le influenze celesti si dispiegano a due livelli, quello universale (trattato nel Libro II) e quello individuale, o 'genetliologico', cioè relativo al genetliaco (trattato nei Libri III-IV). Il primo livello è associato alla dimensione grande della causazione celeste ed è all'origine sia delle differenze nei caratteri di interi popoli sia di grandi eventi collettivi, quali guerre, pestilenze e così via. Il secondo livello è all'origine del 'temperamento proprio' degli individui; esso, influendo fisicamente sulla mistura del seme, è all'origine delle variazioni interne all'identità specifica degli uomini e spiega così le differenze nei caratteri individuali, cui è collegato il corso della vita di ciascuno nel mondo.
Coerentemente con la netta separazione tra cielo e Terra, caratteristica della sua cosmologia, per Tolomeo la causazione astrologica non costituisce una catena causale completamente unificata. I cieli compiono eternamente il loro "destino divino e indeviabile", e influenzano causalmente ciò che accade sulla Terra, ivi compresa la costituzione del temperamento proprio individuale, ma la catena delle cause non è completamente chiusa, per così dire, verso il basso e la materia. Ciò che Tolomeo sembra voler dire si può chiarire con un esempio: un frutto, formatosi con la disposizione a maturare, può marcire per cause esterne, e marcirà certamente se esse sono grandi, ma è possibile che maturi, se sono piccole. Ci sono interstizi d'indeterminazione a livello della piccola causalità nei quali un individuo, una volta formatosi, può divenire una sorgente in certa misura autonoma del proprio agire; egli, impotente rispetto alla scala grande della causalità, può tuttavia deviare il corso naturale della vita nella scala piccola, se si danno le condizioni favorevoli e se è presente il sapere che gli consente di agire nella direzione voluta. Tolomeo dunque non è fatalista, né determinista; in particolare, non è determinata la presenza del sapere che consente di opporsi alle cause piccole (I, 3).
Il titolo originale della Geografia (in 8 libri) era Guida alla rappresentazione grafica della Terra. All'inizio egli distingue la geōgraphía dalla chōrographía; con quest'ultimo termine l'autore intende la rappresentazione grafica di regioni sufficientemente piccole, tali da non presentare gravi problemi quanto alle distorsioni prodotte con la riproduzione in piano della superficie sferica della Terra. Questi problemi però non sono più ignorabili se si vuole produrre una rappresentazione soddisfacente di tutta la Terra allora in qualche misura conosciuta (più di un quarto della superficie sferica). Tolomeo propone a questo scopo una configurazione nella quale i meridiani sono rappresentati da raggi originati da un centro comune, i paralleli da archi di cerchio con lo stesso centro, e dove sono conservate le distanze lungo i meridiani e il parallelo di Rodi (36° N) ed è conservato il rapporto delle distanze sul parallelo 63° N (il limite settentrionale del mondo conosciuto) rispetto a quelle sull'equatore. Fin qui, si tratta di una proiezione conica; a sud dell'equatore, dove le distorsioni diventerebbero troppo grandi ed entrerebbero in conflitto con le apparenze di una mappa disegnata su una sfera, Tolomeo, a spese della coerenza matematica, divide il parallelo 16°25′ S (il limite meridionale del mondo conosciuto) come se si trovasse a nord, ottenendo così una restrizione progressiva delle distanze dei meridiani sulla carta ed evitando in questo modo che la sua mappa entri in conflitto con la mappa osservata su una sfera. Egli propone poi una seconda configurazione, che è soltanto un'approssimazione a una proiezione conica, ma che ha un grado ancora maggiore di somiglianza con le apparenze (I, 21-24). In base a questa seconda configurazione saranno spesso disegnate le mappe del Tardo Medioevo e del Rinascimento.
Nei restanti libri sono date indicazioni circa la longitudine e la latitudine per 8100 località, da collocare sulle configurazioni proposte. In linea teorica i due dati sono conoscibili mediante l'astronomia, ma di fatto ciò per le longitudini era difficilissimo (richiedeva l'osservazione di una stessa eclisse da località differenti) ed era piuttosto raro anche per il caso più facile delle latitudini. In effetti, i valori indicati sono quasi sempre ricavati da resoconti di viaggiatori, con una conseguente imprecisione. Nella Geografia si vedono forse nel modo più chiaro alcune delle caratteristiche generali del lavoro scientifico di Tolomeo: è sempre elaborata una quantità grandissima di materiale e di dati, e c'è sempre uno sforzo di adattamento della costruzione al livello dato di accuratezza nelle misurazioni disponibili.
L'armonica
I tre libri degli Armonici sono redatti in una situazione peculiare, cioè in presenza di due tradizioni musicologiche rivali entrambe consolidate, ossia quella degli aristosseniani (cioè di quanti si rifacevano all'aristotelico Aristosseno di Taranto) e quella dei pitagorici; si tratta di una contrapposizione che risaliva al IV sec., ma si noti che all'epoca di Tolomeo il pitagorismo era ormai un'ala del platonismo. Tolomeo prende le mosse in questo contesto e si colloca piuttosto dalla parte dei secondi, ma con una importante presa di distanza su un punto di metodo centrale.
Le due trattazioni (per un'esposizione più approfondita v. cap. XXVII) condividevano la convinzione di base secondo la quale l'ambito di studio dell'armonica, sebbene sia da noi esperito nella produzione musicale, non è l'esito di una costruzione umana; è invece oggettivo e reale, e l'indagine scientifica ne scopre la struttura interna. Il campo dei fenomeni musicali si disegna entro il campo più generale dei fenomeni sonori; vi accediamo dunque mediante la percezione auditiva, ma tale capacità percettiva non si limita a discriminare i suoni in base alla loro differente altezza (oltre che secondo altre differenze quantitative, che però non sono fondamentali dal punto di vista musicale); l'orecchio, infatti, è in grado già inizialmente di avvertire entro i suoni le sequenze sonore melodiche, e ci fornisce dunque le prime grandi linee del campo di indagine.
Di qui in avanti le due tradizioni divergevano quanto alla concezione dell'oggetto dell'armonica e del modo di trattarne. Gli aristosseniani rappresentavano l'aspetto quantitativo dello spazio musicale come un continuo quasi lineare sul quale le note erano segnate e gli intervalli erano misurati in base alle differenze di altezza, e le note erano identificate più per la loro funzione melodica che per i valori numerici a esse associabili. A questo aspetto tecnico della loro armonica era collegata la concezione per cui le strutture del campo musicale ‒ ciò che per la scienza si trattava di conoscere ‒ erano costituite da relazioni irriducibilmente musicali, rispetto alle quali gli aspetti quantitativi erano secondari. Questi aspetti quantitativi erano certamente considerati e studiati, ma non erano stimati di per sé esplicativi; all'incirca come, per un aristotelico, gli aspetti quantitativi della materia non erano di per sé sufficienti per le spiegazioni richieste nelle indagini sulla Natura. Di contro, per i pitagorici gli aspetti quantitativi del campo musicale erano centrali. Essi rappresentavano gli intervalli tra le note mediante rapporti di numeri, che esprimevano le misure dei rapporti delle grandezze fisiche all'origine dei suoni. Tali rapporti numerici costituivano la struttura essenziale del campo di indagine dell'armonica; la melodicità di certe sequenze di suoni per i pitagorici era non soltanto dovuta al loro essere la traduzione e manifestazione percepibile di quei rapporti, ma ne era anche spiegata. I principî e le strutture dell'armonia erano di ordine matematico e dunque erano passibili di una separata ricostruzione razionale. In questa concezione si poteva pensare, come effettivamente essi facevano, che l'ordine proprio dell'armonia si integrasse con gli ordini propri dell'anima e dei cieli in un comune ordine matematico fondamentale.
Come si è detto, Tolomeo si colloca piuttosto dalla parte dei pitagorici; egli ritiene infatti che sia inammissibile rappresentare gli intervalli tra le note come differenze, e che invece sia corretto soltanto esprimerli come rapporti di numeri. Soprattutto, ritiene che ci sia una classe definita di rapporti numerici, costituente il fondamento per tutti i rapporti armonici, e che prima di tutto questa deve essere stabilita dall'indagine. Egli condivide inoltre la convinzione che la base matematica dell'ordine dell'armonia sia in qualche modo comune con l'ordine dell'anima e dei cieli (nell'ultima parte del Libro III cerca in effetti di tracciare delle analogie tra le articolazioni dell'armonia, dell'anima e dei cieli). Agli aristosseniani riserva le sue critiche più aspre (I, 2); nelle loro indagini essi si valgono "soltanto delle pratiche manuali e del mero e irrazionale esercizio della percezione" e si servono della "ragione" (lógos) soltanto come di un "accessorio" (párergon). Introduce poi la confutazione delle loro teorie con un commento sprezzante: "ammettendo che essi si siano mai impegnati nello studio teorico della musica" (I, 9).
D'altra parte, Tolomeo sottolinea una differenza importante fra il suo punto di vista e quello dei pitagorici: il loro approccio, dice, è "troppo teorico" (theōrētikṓteron; I, 2). Questi in effetti avevano mirato a determinare i rapporti armonici fondamentali riconducendoli entro alcune classi specifiche di rapporti numerici; avevano quindi inteso che tutti i rapporti armonici ‒ non soltanto quelli di base, ma anche quelli composti da questi ‒ rientravano nelle stesse classi di rapporti numerici. La conseguenza implicita era l'esclusione dall'ambito dei rapporti armonici di tutti quei rapporti composti la cui espressione numerica non poteva essere ricondotta a quelle classi di rapporti numerici cui appartenevano i rapporti fondamentali. Più precisamente, secondo la teorizzazione pitagorica ogni rapporto armonico doveva essere esprimibile o nella forma (n+1)/n (il cosiddetto 'epimorico' o 'superparticolare') oppure nella forma mn/n ('multiplo'). Ne seguiva l'esclusione dai rapporti armonici di tutti i rapporti composti irriducibili a una di quelle due forme, e ciò entrava in conflitto con quanto diceva l'orecchio educato, che riconosceva come armonici numerosi rapporti composti irriducibili. Il caso più notevole (I, 6) era dato dall'accordo di ottava più quarta, che chiaramente l'orecchio riconosceva come armonico, ma che i pitagorici non potevano riconoscere come tale, perché la sua espressione numerica era 8/3, irriducibile sia alla forma epimorica che a quella multipla.
Questa difficoltà era già stata osservata e discussa prima di Tolomeo. Una replica dei pitagorici era stata che nell'indagine la percezione aveva un ruolo soltanto iniziale, quello di fornire uno stimolo alla ragione, la quale doveva poi rivolgersi a un ambito di oggetti, quello matematico e razionale, intrinsecamente separato dalla percezione stessa; se accadeva che la costruzione razionale e matematica entrasse in conflitto con la percezione, ciò si spiegava con la non correttezza della percezione, che pertanto andava rifiutata. Tale linea di difesa della tradizione musicologica pitagorica si rifaceva a una lettura possibile di alcuni passi di Platone (si può pensare, per es., al Timeo, dove Platone dice che vediamo l'elemento terra coinvolto nel ciclo delle trasformazioni, ma poi costruisce una teoria geometrica degli elementi in base alla quale la terra è esclusa da tale ciclo e ne conclude che in questo caso c'è una scorrettezza nella presentazione percettiva). Una simile replica è però inammissibile per Tolomeo; l'armonica, come in generale la scienza, non può entrare in conflitto con i fenomeni riconosciuti dalla grande maggioranza, in particolare da coloro la cui percezione è educata. In effetti, egli inizia gli Armonici assegnando alla facoltà dell'udito e alla ragione ruoli specifici e complementari. L'udito fornisce i lineamenti grezzi (holoscherḗs) e approssimati (sýnengys) del campo; non è di per sé capace di ricostruire la forma e l'ordine razionale, che pure sono già sottesi a quei lineamenti approssimati. Tale operazione spetta alla ragione, che perviene alla forma ‒ in questo caso i rapporti numerici ‒ a partire da quanto fornitole dalla percezione; la percezione, una volta che la ragione abbia assolto a questo ruolo, è in condizione di riconoscere nel proprio oggetto un'approssimazione a un oggetto razionale, non diversamente da come la vista riconosce, mediante il compasso, i propri cerchi come approssimazioni al cerchio "realmente preciso". Separare radicalmente i rapporti numerici sottesi all'armonia dalle sequenze sonore avvertite come armoniche da tutti, in particolare da tutte le persone il cui udito è stato educato, è altrettanto inammissibile quanto negare la riconoscibilità del cerchio matematico nelle sue approssimazioni visive. La percezione educata mantiene dunque un ruolo di controllo sulle costruzioni razionali; se gli esiti di una costruzione matematica e razionale entrano in conflitto con la percezione musicale, allora, anche se tale costruzione è elegante e matematicamente corretta, le assunzioni su cui si è basata devono essere sbagliate o almeno inadeguate. Per queste ragioni il metodo dei pitagorici è sbagliato, perché "troppo teorico"; questa scorrettezza di metodo ha reso possibile che essi ponessero per l'armonica principî specifici inadeguati. Ciò non impedisce tuttavia a Tolomeo di sentirsi piuttosto vicino ai pitagorici, perché, una volta rielaborata in modo soddisfacente la loro teoria delle divisioni armoniche, può continuare a condividerne le convinzioni più generali, particolarmente quella per cui sono matematiche le strutture fondamentali dell'armonia. Si può dire ‒ un poco schematicamente ‒ che il Tolomeo degli Armonici si colloca in quell'ala del pitagorismo-platonismo per la quale valeva, nelle scienze, l'impegno e il vincolo alla salvezza dei fenomeni (non differentemente per l'armonica di quanto valesse per l'astronomia matematica).
Tecnicamente (v. cap. XXVII) Tolomeo risolve difficoltà, quali quella costituita dall'accordo di ottava più quarta, costruendo e definendo gli intervalli di base in modo tale che i requisiti della loro forma aritmetica non debbano estendersi ai composti, e gerarchizzando, per così dire, gli intervalli secondo una maggiore o minore melodicità; in tal modo quelle difficoltà sono risolte dissolvendole ed egli può pensare d'incorporare nella sua teoria un'ampia varietà di sistemi. Di qui prosegue poi, nel Libro II e nella prima parte del Libro III, discutendo e mirando non soltanto a organizzare i diversi temi della musicologia contemporanea, ma anche ad assimilare per quanto possibile le pratiche musicali presenti ai suoi tempi.
Va sottolineato un ultimo aspetto della trattazione tolemaica, cioè che l'orecchio, anche se educato, non può da solo emettere il giudizio percettivo che gli si richiede; in particolare, da solo esso può dare soltanto valutazioni quantitative-comparative molto approssimative e molto al di sotto di quanto necessario per i controlli richiesti. È allora indispensabile che siano sottoposte al suo giudizio sequenze sonore delle quali si conoscano già, indipendentemente, sia i rapporti di grandezza tra suoni sia i rapporti numerici che li esprimono; in tal modo l'orecchio assolverà alla funzione richiestagli, riconoscendo come all'unisono o concordanti o melodici o discordanti rapporti determinati. A questo scopo è necessario un apparato strumentale basato teoricamente su una regola di collegamento tra i rapporti di altezza dei suoni e altri rapporti tra grandezze fisiche indipendentemente producibili e controllabili. Il collegamento che Tolomeo stabilisce, sulla base di una breve analisi della fisica dei suoni (I, 3), è tra i rapporti di altezza dei suoni e quelli di lunghezza tra corde vibranti; descrive poi accuratamente il suo principale apparato strumentale, il monocordo (I, 8; in seguito descriverà anche strumenti derivati più complessi). Si tratta essenzialmente di una corda di una certa lunghezza tesa su un regolo graduato finemente; collocando su un dato punto del regolo un 'ponte' che bloccasse la corda sul punto corrispondente, si ottenevano due segmenti di corda che vibravano separatamente; così, leggendo sul regolo il rapporto di lunghezza dei due segmenti, si ottenevano i valori numerici che esprimevano il rapporto di altezza dei suoni prodotti dalle rispettive vibrazioni. In tal modo il giudizio percettivo poteva controllare rapporti determinati.
Sia la correlazione tra i rapporti di altezza dei suoni e quelli di lunghezza delle corde, sia il monocordo risalivano a molto prima di Tolomeo. Ciò che gli è caratteristico ‒ e lo distingue da tutti gli altri musicologi dell'Antichità ‒ è l'attenzione con cui egli descrive i particolari della costruzione degli apparati strumentali, motivata dalla preoccupazione che nell'uso di essi non intervengano fattori distorsivi degli effetti sonori, quindi tali da vanificare i giudizi percettivi richiesti. Con ogni verosimiglianza, gli usi pretolemaici del monocordo avevano avuto un intento prevalentemente didattico e illustrativo; di contro, la cura di Tolomeo riguardo ai suoi apparati sembra confermare che egli li pensasse anche come strumenti scientifici, cioè come apparecchi per eseguire esperimenti di controllo. Questo, di nuovo, è peculiare dei suoi Armonici (anche se difficilmente i suoi apparati strumentali potevano di fatto assolvere alla funzione che egli assegnava loro).
L''Ottica'
Forse ultima cronologicamente delle opere tolemaiche, e certamente seconda soltanto all'Almagesto quanto a importanza scientifica, fu l'Ottica, rimastaci soltanto in una traduzione latina medievale di una traduzione araba e mancante del primo libro e della parte finale del quinto e ultimo libro. In essa Tolomeo produce essenzialmente una teoria della visione. Non si tratta dunque di uno studio sulla luce e sui suoi comportamenti fisici; la luce è presente soltanto marginalmente, come condizione della visibilità degli oggetti. L'Ottica contiene inizialmente (per la parte conservataci) una breve sezione su ciò che si vede (II, 4-21) e per il resto verte sul modo dell'atto visivo, su come esso produce la conoscenza di una classe di proprietà degli oggetti e su come abbiano luogo le illusioni e gli errori nella visione.
L'atto percettivo della visione presume, per Tolomeo, come sua base un processo fisico, cioè un movimento nella corporeità. Tale processo è pensato come l'estromissione dall'occhio di un cono visivo, il quale raggiunge l'oggetto visto, ne viene dunque a contatto e si ferma contro la sua superficie senza penetrarlo. Il cono visivo ha una consistenza fisica, al modo all'incirca di un flusso fluido continuo (c'è forse qui un'influenza stoica); esso può essere analizzato e risolto in un fascio di raggi discreti, secondo una modalità già messa in opera nell'Ottica di Euclide. A differenza però di Euclide, il cono non consiste di raggi discreti; tale risoluzione è soltanto lo strumento per la sua analisi. Ciò che "realmente" (vere) si vede sono dunque i corpi contro cui i raggi del cono si fermano; essi sono i "corpi compatti in luce" (lucida spissa); la compattezza spiega l'arresto e l'essere in luce è l'ulteriore condizione della visibilità. Questa è peraltro la base fisica di un atto, quello visivo, che è essenzialmente percettivo. Si ha la percezione in quanto nel contatto si vedono "immediatamente" (primo) i colori; "in modo mediato" (sequenter) si vedono la grandezza, la forma, la posizione, il moto e la quiete (II, 4-6); qui chiaramente Tolomeo s'ispira alla distinzione aristotelica tra i sensibili propri e specifici di ciascun organo di senso e i sensibili comuni. Il colore, il sensibile proprio della vista, è una proprietà reale del corpo visto, ossia non esiste soltanto nell'interazione tra chi vede e ciò che è visto. Nell'atto visivo quella parte del cono che entra in contatto con la superficie colorata subisce una "passione" (passio), nel senso che ne è colorata, e trasmette così all'occhio il contorno della superficie, quale appare in base all'angolo sotto cui è vista (II, 8-16). Questa è la fase meramente sensitiva dell'atto percettivo; segue poi quella propriamente percettiva, la quale contiene una componente embrionalmente inferenziale, mediante la quale si perviene alla conoscenza degli altri visibili. Alla grandezza si perviene in quanto secondo Tolomeo ogni raggio (un processo fisico, si ricordi) porta con sé in certa misura il senso della quantità del percorso compiuto, quindi dà in certa misura anche la distanza; così la grandezza propria del corpo visto è valutabile e lo è in linea di principio esattamente anche se il corpo si presenta obliquamente, in quanto i diversi raggi danno in questo caso una differente misura della distanza. In questo modo si perviene nella visione anche alla forma propria dell'oggetto. Del pari, la posizione e il moto sono ricavabili, in quanto il cono visivo ha un orientamento, riferito al proprio asse centrale (II, 20, 26-27, 52-62).
Questa analisi vale per un cono solamente, dunque per un occhio solo. Caratteristica dell'ottica tolemaica è che non soltanto sono affrontati i problemi dati dalla visione binoculare, ma anche che la spiegazione del suo funzionamento sia basata e illustrata servendosi di un insieme di esperimenti. "La Natura ‒ dice Tolomeo (II, 28) ‒ ha fatto la vista doppia, affinché vediamo meglio e la nostra visione sia regolata e definita". Ciò presume, affinché non si veda doppio, che gli assi dei due coni convergano sullo stesso punto della superficie dell'oggetto e che le basi dei due coni coincidano. Tolomeo parte da questo assunto, e lo conferma mediante un apparato sperimentale nel quale diversi bastoncini diversamente colorati e a distanze variate sono fatti guardare sia da un occhio sia da due, in modo sia da controllare sperimentalmente il funzionamento normale della visione binoculare, sia da produrre artificialmente l'effetto della visione doppia, o diplopia, che si ha nei casi in cui i due assi non convergono (II, 30-45).
Dopo aver prodotto la teoria della visione e di come si pervenga a percepire le proprietà effettive degli oggetti, Tolomeo compie un'analisi molto lunga delle diverse circostanze, cause e modi in cui l'atto visivo sfocia in "illusioni" o "errori" (deceptiones). Ciò può dipendere da fattori relativi o alla fase fisica dell'atto o a quella sensitiva o a quella propriamente percettiva e 'inferenziale'; d'altra parte, può trattarsi sia di fattori oggettivi sia di fattori collegati al funzionamento della vista. Entro questa sezione ricadono in linea di principio i fenomeni della riflessione e della rifrazione: in entrambi i casi, infatti, gli oggetti sono visti là dove non sono. Tolomeo, tuttavia, dedica separatamente a questi fenomeni tutta la seconda parte della sua Ottica (Libri III-V), sia perché entrambi sono passibili di una approfondita trattazione in termini matematici, sia perché essi hanno in comune la loro spiegazione peculiare; si tratta sempre di una "rottura" (fractio) del raggio visivo, che nella riflessione è bloccato dalla superficie e, per così dire, rimbalza, mentre nella rifrazione è rallentato, per la densità del corpo, e devia.
I tre principî della teoria della riflessione sono esposti all'inizio del Libro III. Per il primo, "gli oggetti visti negli specchi appaiono sul prolungamento del raggio visivo che li raggiunge tramite la riflessione"; in altre parole, il raggio muove dall'occhio A (fig. 10) e, spezzandosi in C, sulla superficie MN dello specchio, raggiunge l'oggetto O, che tuttavia gli appare sul prolungamento CE di AC. Per il secondo, "i punti [dell'oggetto] visti negli specchi appaiono sulla normale condotta dall'oggetto alla superficie dello specchio e prolungata", cioè sul prolungamento di OP. Per il terzo, "la disposizione del raggio che connette l'occhio allo specchio e lo specchio all'oggetto è tale che ciascuno dei due tronconi contiene il punto in cui c'è la frattura, e produce angoli uguali con la normale allo specchio in quel punto". In altri termini, gli angoli AĈB e BĈO sono uguali, per BC perpendicolare alla superficie dello specchio; in tal modo il punto E risulta completamente determinato (III, 3). Tolomeo aggiunge che nel caso di superfici curve OE è normale alla superficie tangente in C, ed esplicita un ulteriore assunto latente nella sua teoria, cioè che tutti i segmenti di raggio giacciono su uno stesso piano, normale alla superficie di riflessione (III, 5).
Nell'adozione dei tre principî Tolomeo non era originale (mentre forse lo fu nelle precisazioni ulteriori). La sua originalità consistette invece nel fatto che cercò per essi una conferma sperimentale. Il primo principio, per esempio, è confermato coprendo diversi punti dell'immagine sullo specchio, poi scoprendoli e osservando che essi conservano l'allineamento con il raggio proveniente dall'occhio; il secondo drizzando un regolo sulla superficie dello specchio e osservando che esso e il suo prolungamento appaiono sempre su una sola linea retta (III, 4). Ancora, che il terzo principio valga anche per tutti gli specchi curvi è confermato mediante un esperimento, che mostra come l'uguaglianza di quei due angoli si mantenga anche se si sostituisce a un iniziale specchio piano uno specchio convesso o concavo (III, 8-12). In generale, l'intera trattazione degli specchi curvi, molto complicata, è caratterizzata dall'alternanza di analisi geometriche e di esperimenti confermativi.
La componente sperimentale è ancora più accentuata nella sezione sulla rifrazione. In effetti, l'impianto analitico è lo stesso di quello dell'indagine sulla riflessione, ma qui il raggio visivo penetrando nell'acqua si spezza e si flette verso la normale, quindi forma un angolo di rifrazione differente da quello di incidenza; ora, i due angoli presentano "una determinata relazione quantitativa" (similitudinem quandam et quantitatem; V, 2), di cui si tratta di stabilire la regola, e ciò non può essere tentato se non mediante esperimenti. Il primo, e più tipico, consiste (V, 8-11) nel prendere un disco metallico d con i bordi graduati, dividerlo in quadranti, collocarvi due contrassegni mobili sui bordi di due quadranti opposti e un terzo al centro, e immergerlo nell'acqua nel modo illustrato nella fig. 11, dove MN è la superficie dell'acqua, e A l'occhio; si sposta il contrassegno F fino ad allinearlo sulla visuale che va dall'occhio A al centro C del disco e si muove poi il contrassegno sott'acqua, finché esso appaia allineato con l'occhio e gli altri contrassegni, cioè finché esso appaia nella posizione X (pur trovandosi realmente nella posizione O); infine, estraendo il disco, si ha la misura dell'angolo di rifrazione, r, per l'angolo di incidenza, i (V, 8-11). Tolomeo ci informa di aver compiuto numerosi esperimenti con mezzi di diversa densità, cercando di determinare le regole della differenza dei due angoli nei diversi casi. Tolomeo conclude poi i suoi esperimenti enunciando soltanto una regola generale molto debole: la differenza tra i e r cresce con il crescere di i (V, 34). Allorché cerca di determinare più strettamente questa dipendenza, egli procede partendo dall'osservazione del rapporto tra i due angoli per i piccolo (10°) e poi per ogni intervallo di 10° di i corregge la proporzione iniziale, facendo decrescere progressivamente il valore di r relativamente a i, mediante l'applicazione a ogni intervallo di una differenza seconda costante (0,5°). Si tratta di un'approssimazione piuttosto grezza, che procede a salti molto grandi, muovendo da valutazioni che Tolomeo stesso qualifica come approssimative (ad prope; V, 11). Invero, i dati osservativi presenti nelle tavole che si trovano in quest'ultima sezione dell'Ottica appaiono aggiustati, in modo da conformarsi al procedimento aritmetico con cui le tavole sono generate. Va peraltro sottolineato che Tolomeo non formula una regola generale precisa, del tipo della moderna legge della rifrazione.
Vista nel suo insieme, l'Ottica tolemaica raccoglie e incorpora una tradizione precedente di indagini, che si era articolata in tre livelli di crescente complessità: l'ottica in senso stretto, che studiava in generale la visione diretta, la catottrica, che studiava la riflessione negli specchi, e la diottrica, il cui ambito era costituito prevalentemente dalla rifrazione. Se la documentazione rimastaci non c'inganna, gli studi precedenti avevano avuto una impostazione quasi esclusivamente matematica. Ciò che sembra peculiare di Tolomeo è soprattutto l'aver inserito questa tradizione in un quadro di indagine più ampio, ossia, da un lato, l'aver collegato le analisi geometriche del cono visivo con lo studio del funzionamento 'fisiologico' della visione, in particolare con il problema sollevato dalla binocularità, e, dall'altro lato, l'aver confrontato l'intera sua teorizzazione con considerazioni di tipo sperimentale. In effetti nell'Ottica sono esposti una ventina di esperimenti e spesso quest'opera è citata quando si vuole smentire l'opinione alquanto diffusa per cui nella scienza antica l'esperimento era assente.
La filosofia di Tolomeo
Tolomeo è uno scienziato, non un filosofo. Più volte si sottrae dichiaratamente alle controversie dei filosofi. Così, nel proemio dell'Almagesto dichiara di non aver voluto affrontare la discussione teologica relativa alla "prima causa del primo movimento", perché intrinsecamente congetturale e controversa (I, 1); del pari, nello scritto Il criterio e l'egemonico rifiuta di discutere la questione se l'anima sia incorporea oppure un tipo particolare di corpo, giudicandola una logomachia filosofica (4-7). Egli ha tuttavia una propria filosofia, non soltanto in quanto ebbe una concezione della scienza che andava sviluppando, ma anche in quanto ne definì il senso e il valore, e delineò in base a essa un mondo.
Nel proemio dell'Almagesto Tolomeo inizia citando Aristotele e dice (come si è già accennato) che le cose che sono, sulle quali dunque verte qualunque indagine, sono costituite da forma, materia e movimento. S'allontana però rapidamente da Aristotele in quanto distingue le proprietà materiali delle cose da quelle formali, caratterizza, non aristotelicamente, le prime come oscure e fa coincidere le seconde con le proprietà trattabili matematicamente, rendendole perciò gli unici veri e propri oggetti scientifici e identificando così le matematiche come le sole vere e proprie scienze. l tempo stesso, egli sembra pensare, aristotelicamente, che gli enti matematici esistano come proprietà delle cose, ma soprattutto recupera Aristotele sul terreno fisico-cosmologico. Riprende infatti l'elementarizzazione della corporeità esposta nel De caelo ‒ basata sulla distinzione fondamentale tra corpi che naturalmente si muovono di moto circolare e corpi che naturalmente si muovono di moto rettilineo ‒ e la nozione di un corpo specifico per i cieli, l'etere. Dato che tale elemento è privo delle proprietà oscure della materia, i cieli rientrano immediatamente e senza residui nell'ambito delle matematiche, che hanno in essi la zona naturale della loro applicazione elettiva; mathēmatikós significa immediatamente anche "astronomo". Così, come per Platone e Aristotele, i cieli sono immortali e divini; la loro indagine, restando scientifica, può tenere il posto dell'incerta teologia dei filosofi.
Tolomeo, dunque, non si pensa davvero come uno scienziato che si limita ad applicare alle cose naturali un apparato matematico ricavandone previsioni (anche se si può dire che di fatto proceda in questo modo nell'Almagesto); ciò che ai suoi occhi fonda questa applicazione e ne spiega il successo è la sua cosmologia. Essa riprende da quella aristotelica, cui si rifà, la spaccatura dinamica tra cielo e Terra, che diventa un tratto centrale del mondo tolemaico, quello per cui, tra l'altro, è possibile la proposta della 'dinamica' vitalistica celeste nelle Ipotesi planetarie. Essa sta alla base dell'assegnazione di senso e di valore alla scienza, per tutti e per chi la pratica. Per tutti, dato che "in tutti i casi lo scopo proprio dello scienziato sta nel mostrare che le opere della Natura sono state fatte con una ragione e una causa ordinata", come è detto negli Armonici (I, 2), in un passo in cui tale scopo è assegnato in modo precipuo congiuntamente all'astronomia e all'armonica, in quanto entrambe trovano, in due differenti aree naturali, l'ordine realmente sotteso agli oggetti delle percezioni visive e auditive, inizialmente avvertito da esse, ma soltanto in modo inadeguato. Per chi pratica la scienza, perché così facendo la sua anima acquisisce, insieme con l'intelligenza dell'oggetto, anche una disposizione complessiva simile ad esso, dunque bella, come è detto nel proemio dell'Almagesto (I, 1) e ripetuto negli Armonici (III, 3).
La scienza ha dunque per Tolomeo un valore che riguarda globalmente l'anima; a questa linea di pensiero si collega il legame che egli tende a stringere tra cielo e anima, sulla scia di una tradizione ormai secolare. Nella lunga parte finale degli Armonici stabilisce inizialmente una molteplicità di corrispondenze tra le parti e le forme dell'armonia, da un lato, e le virtù e i tipi dell'anima dall'altro lato (III, 3-7), combinando in un modo non sempre chiaro ingredienti delle psicologie platonica, aristotelica e stoica; di qui passa poi a stabilire un'ulteriore serie di corrispondenze tra le parti e le forme dell'armonia e diversi aspetti delle disposizioni e dei moti celesti (III, 8-16). Così ottiene, tramite l'armonia, una sorta d'integrazione delle strutture dell'anima umana con le forme dei cieli; questa operazione può essere considerata come complementare a quella condotta nel suo trattato astrologico, la Tetrabiblos, dove ‒ come si è detto ‒ è svolta la trattazione delle influenze celesti sulla costituzione del temperamento proprio di ciascun individuo e sugli eventi che ne accompagnano la vita. In quest'opera Tolomeo legittima teoricamente la medicina astrologica, ossia una medicina che si basava sulla pretesa di conoscere, per via astrologica, sia la costituzione peculiare di ciascuno sia gli eventi imminenti, e che mirava a curare rinforzando quelle componenti della disposizione individuale capaci di fronteggiare effetti negativi derivanti dalle influenze celesti (I, 3). L'astrologia dunque apporta alla scienza un'altra dimensione di valore. Tolomeo poi ne aggiunge una terza: poiché di fronte a eventi indeviabili la previsione astrologica consente alla nostra anima una sorta di esercizio anticipato della loro presenza, quindi una sorta di abitudine anticipata, e per questa via ci rende possibile accoglierli mantenendo una condizione psichica di pace interna e di equilibrio stabile (I, 3). Si noti come Tolomeo, nell'assegnare alla scienza valore nell'etica e nella vita, si valga di argomenti di provenienza diversa; mentre l'ultimo argomento appare di ispirazione stoica, è difficilmente compatibile con lo stoicismo l'idea di una medicina che, sapendo prevedere le influenze celesti, ne può sviare gli effetti; appare poi d'ispirazione platonica la concezione dell'assimilazione dell'anima, nella scienza, ai suoi oggetti e alla loro bellezza.
Nell'unico e breve scritto di argomento filosofico, Il criterio e l'egemonico, Tolomeo delinea sommariamente una sorta di teoria dell'atto di giudizio umano. Si può dire che l'Ottica tratti scientificamente e per esteso una piccola sezione di quanto è delineato in questo scritto e tra le due opere c'è una convergenza di massima (anche se non sembra perfetta, a meno che il testo rimastoci, la traduzione di una traduzione, non c'inganni). In un atto di giudizio umano un agente (l'intelletto) giudica un oggetto in vista della verità servendosi degli organi di senso e con la ragione (lógos); sono questi i cinque elementi strutturali del giudizio. L'organo di senso, venendo a contatto con l'oggetto, subisce una passione e ne trasmette l'impressione all'intelletto, che con la ragione giudica riguardo a ciò che ha dato origine all'impressione (1-3). Ciò che qui non emerge è la fase inferenziale presente, sia pure embrionalmente, nell'Ottica già nella visione, nel momento in cui la vista risale dalla sensazione del colore alla grandezza, alla forma e alla posizione dell'oggetto; in base a Il criterio non sembra possibile attribuirla a un intervento dell'intelletto, dato che la vista, come le altre percezioni, è comune agli uomini e agli animali, e gli animali non hanno intelletto. Va tuttavia notato che Tolomeo attribuisce (12) a 'ciascuna' delle facoltà sensoriali una sorta di coscienza interna (entòs synaísthēsis) di sé stessa e dei propri movimenti (ciò che si connette bene con il senso della distanza percorsa posseduto dai raggi visivi); inoltre, egli ammette per ciascun organo corporeo una sorta di 'principio direttivo' (è questo il senso di 'egemonico') proprio (13); non sembra difficile inserire qui, ancora nell'ambito della visione, la risalita embrionalmente inferenziale alle proprietà visibili che vanno oltre il colore.
L'intelletto acquisisce i concetti in base alla percezione e alla memoria; a seconda di come giudica con la ragione si ferma al livello delle opinioni o perviene a un abito scientifico. È da rilevare tuttavia che alcuni concetti fondamentali e particolarmente implicati nell'attività scientifica, quali identità e differenza, non sembrano avere un'origine nell'esperienza. Alla fine de Il criterio Tolomeo (13-15) esamina come si coordini la molteplicità dei principî direttivi; a tale scopo introduce una loro gerarchizzazione e aggiunge che, se si prende il termine 'egemonico' in senso stretto, allora ce n'è propriamente soltanto uno, quello cui tutti gli altri sono subordinati. Tuttavia, sdoppia immediatamente questa gerarchia, dato che da un lato c'è un principio che coordina tutti gli egemonici specifici dei vari organi in vista del mero vivere e dall'altro lato ce n'è uno che li coordina in vista del vivere bene; resta tuttavia una subordinazione (che sembra più di diritto che di fatto) del primo al secondo. Questa gerarchia di ordine psichico trova poi una collocazione differenziata nella struttura corporea; mentre il principio direttivo del mero vivere ha la sua sede nel cuore, quello del vivere bene l'ha nel cervello, dove si trova la facoltà di pensare. La sede del cervello, dice Tolomeo, "la testa, è nell'uomo ciò che il cielo è nel mondo" (15), aggiungendo che il secondo posto nella gerarchia relativa al vivere bene spetta alla vista e all'udito, per l'apporto di queste due facoltà percettive all'attività teoretica e giudicatrice del pensiero; per questo i loro organi sono collocati così vicino al cervello. Negli Armonici il valore privilegiato di vista e udito è sottolineato ripetutamente ed è motivato con il loro essere all'origine delle due scienze principali, l'astronomia e l'armonica. È facile sentire in tutto questo l'eco di molti passi platonici, in particolare del Timeo.
Bibliografia
Barker 1984-89: Greek musical writings, edited by Andrew Barker, Cambridge- New York, Cambridge University Press, 1984-1989, 2v.; v. I: The musician and his art, 1984; v. II: Harmonic and acoustic theory, 1989.
Boll 1894: Boll, Franz Johannes, Studien über Claudius Ptolomäus, “Jahrbücher für classische Philologie”, Suppl., 21, 1894, pp. 51-244.
De Pace 1981-82: De Pace, Anna, Elementi aristotelici nell’Ottica di Claudio Tolomeo, “Rivista critica di storia della filosofia”, 36, 1981, pp. 123-138; 37, 1982, pp. 243-276.
Duhem 1908: Duhem, Pierre Maurice Marie, Sózein tà phainómena. Essai sur la notion de théorie physique de Platon à Galilée, Paris, A. Hermann, 1908.
Franco Repellini 1998: Franco Repellini, Ferruccio, L’organizzazione del trattato astronomico nell’antichità, in: Le forme della comunicazione scientifica, a cura di Massimo Galuzzi, Gianni Micheli, Maria T. Monti, Milano, F. Angeli, 1998, pp. 41-56.
Goldstein 1967: Goldstein, Bernard R., The arabic version of Ptolemy’s planetary hypotheses, “Transactions of the American Philosophical Society”, 57, 1967.
Lejeune 1948: Lejeune, Albert, Euclide et Ptolémée, deux stades de l’optique géométrique grecque, Louvain, Bibliothèque de l’Université, 1948.
Lloyd 1978: Lloyd, Geoffrey Ernest Richard, Saving the appearances, “Classical quarterly”, 28, 1978, pp. 202-222, e in: Methods and problems in Greek science, Cambridge-New York, Cambridge University Press, 1991, pp. 248-277.
– 1982: Lloyd, Geoffrey Ernest Richard, Observational error in later Greek science, in: Science and speculation. Studies in hellenistic theory and practice, edited by Jonathan Barnes [et al.], Cambridge-New York, Cambridge University Press; Paris, Éditions de la Maison des sciences de l’homme, 1982, pp. 128-164.
– 1987: Lloyd, Geoffrey Ernest Richard, The revolutions of wisdom. Studies in the claims and practice of ancient Greek science, Berkeley (Calif.), University of California Press, 1987.
Long 1989: Long, A.A., Ptolemy on the criterion. An epistemology for the practising scientist, in: The criterion of truth. Essays written in honour of George Kerferd, edited by P. Huby and G. Neal, Liverpool, Liverpool University Press, 1989, pp. 159-178.
Manuli 1980: Manuli, Paola, Claudio Tolomeo. Il criterio e il principio, “Rivista critica di storia della filosofia”, 35, 1980, pp. 2-26.
Neugebauer 1957: Neugebauer, Otto, The exact sciences in antiquity, Providence, Brown University Press, 1957 (trad. it.: Le scienze esatte nell’antichità, Milano, Feltrinelli, 1974).
– 1975: Neugebauer, Otto, A history of ancient mathematical astronomy, Berlin-New York, Springer-Verlag, 1975, 3 v.
Pedersen 1974: Pedersen, Olaf, A survey of the Almagest, Odense, Odense University Press, 1974.
Sambursky 1962: Sambursky, Samuel, The physical world of late antiquity, London, Routledge & Kegan Paul, 1962.
Simon 1988: Simon, Gérard, Le regard, l’être et l’apparence dans l’optique de l’antiquité, Paris, Éditions du Seuil, 1988.
Smith 1981: Smith, A. Mark, Saving the appearances of the appearances. The foundations of classical geometrical optics, “Archive for history of exact sciences”, 24, 1981, pp. 73-99.
– 1982: Smith, A. Mark, Ptolemy’s search for a law of refraction. A casestudy in the classical methodology of saving the appearances and its limitations, “Archive for history of exact sciences”, 26, 1982, pp. 221-240.
Toomer 1974: Toomer, Gerald J., Ptolemy, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner, 1970-1980, 16 v.; v. XI, 1974, pp. 186-206.
Vegetti 1994: Vegetti, Mario, L’utilità della divinazione. Un argomento stoico in Tolomeo, Tetrabiblos, I 3.5, “Elenchos”, 15, 1994, pp. 219-228.