Scienza greco-romana. Scienza e forme di sapere in Platone
Scienza greco-romana. Scienza e forme di sapere in Platone
Scienza e forme di sapere in Platone
L'atteggiamento di Platone nei confronti del sapere relativo al mondo sensibile è oggetto di valutazioni divergenti. La sua influenza è stata per lo più giudicata negativamente, in quanto la tesi che egli sostiene ‒ e cioè che la vera realtà sia quella delle forme intelligibili, di cui le forme sensibili non sono che immagini ‒ avrebbe più sbocchi verso una metafisica, se non addirittura verso una mistica religiosa, che non verso lo studio dei fenomeni naturali. Da un altro punto di vista, però, può sembrare che l'approccio di Platone precorra la scienza moderna in quanto egli pone la matematica a modello del sapere e descrive in termini matematici la stabilità che si manifesta nel mondo sensibile. Se si ammette che esistono livelli diversi di realtà e che la vera realtà è quella delle forme intelligibili, ne consegue che la conoscenza delle cose sensibili non può essere considerata scienza nel senso stretto del termine. Attingendo alle immagini della realtà sensibile, anziché alla realtà intelligibile, essa può pervenire solamente al verosimile, mentre il vero le sfuggirà sempre. Il suo statuto resta dunque inferiore, e questo nonostante Platone dedichi la maggior parte della sua opera a parlare della realtà sensibile. Sulla base di queste considerazioni va dunque definito l'atteggiamento di Platone nei confronti delle conoscenze della sua epoca (matematica, medicina, ecc.): fu quello di un amatore illuminato o quello di un autentico conoscitore? A questo proposito va innanzi tutto chiarita un'importante evoluzione nel pensiero platonico. In un primo tempo egli, seguendo Socrate, individua un modello rigoroso di approccio alla conoscenza del mondo sensibile nelle téchnai (il termine téchnē designa in greco antico una grande varietà di competenze e di abilità, che va dalle arti figurative sino alla retorica, dalla medicina e dalla navigazione sino all'architettura, e include anche il lavoro dei fabbri, dei falegnami e addirittura dei calzolai). Si tratta di competenze e di pratiche che, in un modo o nell'altro, sono sempre esistite e che si caratterizzano per la loro specializzazione; in quest'ambito nessun esperto rivendica la totalità del sapere. Una téchnē implica il controllo di un sapere specialistico, che cerca di dominare il suo campo d'esperienze mediante procedure razionali. Procedure che possono essere pubblicamente descritte e che devono permettere di ottenere, all'interno dei loro limiti, risultati efficaci. Una téchnē è in grado di rivendicare una vera autonomia in quanto ha un dominio, procedure e risultati propri. Una téchnē, inoltre, può essere oggetto di trasmissione e d'insegnamento, il che implica un accumulo delle conoscenze; essa conferisce, infine, una dignità sociale a chi la pratica.
Nei primi scritti platonici, il richiamo alle téchnai ha due funzioni principali: consente di opporsi efficacemente a qualsiasi tipo di falso sapere, e propone dei modelli di 'saper fare'. Ogni téchnē implica infatti una attività (érgon) che può consistere nella produzione di un oggetto (per es., un flauto, un'imbarcazione), implicare l'uso di questi oggetti (musica, navigazione), o ancora essere relativa alla cura (therapeía) di certi oggetti naturali (campi, bestiame, corpi umani). Nei limiti del campo che le è proprio, la téchnē dispone di una piena conoscenza delle procedure razionali del suo intervento, procedure che è in grado di trasmettere con l'insegnamento; in questa prospettiva, essa presenta un carattere normativo e rivendica ‒ in relazione al suo oggetto ‒ un'efficacia (dýnamis) d'intervento. Le téchnai possono dunque proporsi come modello per l'etica e la politica poiché sono sempre un 'saper fare' e un 'poter fare'.
Ciò detto, a rimettere in discussione l'uso della téchnē come modello del sapere intervengono due problemi: da una parte, gli oggetti di tutte le téchnai dipendono dal mondo sensibile, che è soggetto a un incessante mutamento e, in quanto tale, non può divenire oggetto di pensiero e di linguaggio; d'altra parte, ogni téchnē ha come fondamento la ricerca dell'interesse di colui che la pratica, a differenza di quanto avviene in un certo numero di forme di sapere, per esempio nell'astronomia, ove l'interesse non entra in causa. Ecco perché Platone, senza abbandonare del tutto quel che le téchnai gli avevano dato, si rivolge dopo il Menone verso un altro paradigma: la matematica. La realtà sensibile deve essere provvista di una vera stabilità se si vuole apprenderla intellettivamente e parlarne, e soltanto la matematica mette l'essere umano in grado di apprendere e descrivere questa stabilità. La matematica pura, considerata oggetto di studio di per sé stessa, permette quindi all'anima di sottrarsi al sensibile, e questo anche se nel quadro della pratica greca si dava la preminenza alla costruzione (con riga e compasso) rispetto al calcolo. L'idealità propria della matematica permette a Platone di far capire la necessità dell'esistenza di forme intelligibili, di cui le forme sensibili altro non sono che immagini. Ma non solo: essa infatti, in quanto manifesta quella simmetria che assicura alle realtà percepite dai sensi una vera stabilità, appare come traccia dell'intelligibile nel sensibile. Tutto ciò che l'essere umano può fare è osservare e descrivere questa stabilità nel quadro delle diverse forme di sapere: cosmologia (o astronomia), fisica, chimica, biologia, medicina, psicologia (normale e patologica), botanica, geografia o storia. È utile ricordare, tuttavia, che questo inventario delle diverse forme di sapere ricorre a termini moderni che non si ritrovano in Platone per designare dei saperi costituiti, tranne forse che per l'astronomia e la medicina. Infatti, non esiste in greco nessun termine che corrisponda al 'sapere' in quanto diverso dalla 'scienza' (in greco epistḗmē, termine che Platone riserva alla conoscenza delle realtà vere, rappresentate dalle forme intelligibili).
Platone ammette dunque l'esistenza di realtà separate onde permettere alle cose sensibili, che ne sono le copie, di divenire oggetti di conoscenza e di discorso; egli si accosta inoltre a ogni tipo di conoscenza del mondo sensibile con un rigore e una coerenza propri in primo luogo, direttamente o indirettamente, della matematica.
La dottrina filosofica proposta da Platone è caratterizzata da un doppio rovesciamento. Innanzitutto il mondo delle cose percepite dai sensi non è che una copia delle forme intelligibili (o Idee) che, come modelli delle cose sensibili, costituiscono la vera realtà; a differenza delle cose sensibili, le forme intelligibili possiedono in sé stesse il loro principio d'esistenza. Inoltre, l'uomo non è riducibile al corpo, e la sua vera identità coincide con quel che designiamo col termine 'anima', quale che sia la definizione proposta per questa entità che dà conto ‒ non soltanto nell'uomo, ma anche nell'Universo nel suo complesso ‒ di ogni movimento, sia materiale (crescita, moto locale, ecc.) sia spirituale (sentimenti, percezione sensibile, conoscenza intellettuale, ecc.). È questo doppio rovesciamento, questa doppia trascendenza che, lungo tutto il corso storico della filosofia occidentale, ha permesso di definire la specificità del platonismo. L'ipotesi dell'esistenza di forme intelligibili, che Platone non definisce mai e di cui si limita a richiamare i tratti negativi, consente infatti al filosofo di fondare un'etica, una teoria della conoscenza e un'ontologia.
Realtà, conoscenza, discorso
Dinanzi alla confusione che regna ad Atene, quando l'assetto politico della città crolla sotto i colpi degli avversari e i cittadini tengono discorsi contraddittori sui valori comuni, Platone, pur cercando di continuare l'azione di Socrate, tenta di proporre un discorso politico diverso: un discorso politico fondato su principî morali assolutamente certi, che possano servire a trasformare le città. Ciò spiega perché i primi dialoghi vertano su questioni etiche o politiche. Si tratta di definire le virtù essenziali del perfetto cittadino; tale esigenza implica l'esistenza di norme assolute le quali ‒ perché servano da punti di riferimento per dirigere e valutare la condotta umana ‒ non devono dipendere né dalla tradizione (come quelle trasmesse dai poeti) né da convenzioni arbitrarie (come pretendono i sofisti). Ma questa ipotesi, che rende possibile un sistema etico, rinvia alla sfera epistemologica, come si può constatare nel Menone. Per scoprire e apprendere le norme assolute su cui si fonda l'etica ‒ che in quanto tali non possono essere trovate nel mondo sensibile ‒ si deve ipotizzare l'esistenza di una facoltà distinta dall'opinione: l'intelletto. Ora, la distinzione tra intelletto e opinione comporta la distinzione tra i loro rispettivi oggetti: se dominio dell'opinione sono le cose sensibili immerse nel divenire, sulle quali essa formula dei giudizi, l'intelletto può cogliere realtà immutabili e assolute. In breve, per legittimare dei processi di conoscenza presupposti da esigenze di ordine etico, Platone è indotto a ipotizzare l'esistenza di quelle realtà che sono le forme intelligibili. In questa prospettiva, l'ipotesi dell'esistenza di un mondo di forme intelligibili si presenta come un espediente efficace, ma dalla funzione esclusivamente pratica. Le forme intelligibili certamente danno conto dei processi della conoscenza intellettuale; tuttavia la realtà sensibile non dipende da questi processi di conoscenza. Se, nel mondo sensibile, gli oggetti e le loro caratteristiche si riducono ai risultati transitori di movimenti compositi, indipendentemente dalle necessità dell'etica e dell'epistemologia, l'ipotesi dell'esistenza di un fondamento ontologico s'impone per arrivare a una spiegazione dei fenomeni sensibili i quali altrimenti, lasciati a sé stessi, si dissolverebbero nel Caos (ipotesi considerata in Timaeus, 52 a-b). Si possono conoscere tali fenomeni sensibili e se ne può parlare, soltanto in quanto essi presentano una certa stabilità, quella assicurata dalla loro partecipazione all'intelligibile. Il demiurgo, fissando lo sguardo sulle forme intelligibili nel fabbricare l'Universo, garantisce questa stabilità. Egli rende così possibile, nella città, l'esistenza di norme utili a orientare la condotta umana, individuale e collettiva, poiché risolve ‒ quanto meno in un contesto mitico ‒ il problema della partecipazione delle cose sensibili alle forme intelligibili. L'etica e la politica esigono l'esistenza di un certo ordine, di una certa permanenza nel mondo sensibile; tale doveva essere l'intenzione di Platone nello scrivere il Timeo, che appare in qualche modo come la conclusione di un'elaborazione di cui il Menone, il Fedone, la Repubblica e il Fedro costituiscono le tappe essenziali.
Questa divisione della realtà in modelli, che costituiscono la vera realtà, e in copie, che comportano soltanto una realtà derivata, implica una distinzione strettamente parallela sul piano della conoscenza e del discorso. In proposito, questo brano del Timeo è eloquente: "Così ci conviene distinguere fra l'immagine e il suo modello, poiché i discorsi hanno una certa qual parentela con l'oggetto di cui sono interpreti: e dunque il discorso intorno a ciò che è stabile, fisso in sé stesso, luminoso all'intelletto, esso pure è fisso e incrollabile e, per quanto è possibile, deve essere inconfutabile e incrollabile, e nessuna di queste condizioni deve mancare. Quanto poi al discorso intorno a ciò che raffigura quel modello, e ne è l'immagine, tal discorso sarà verosimile e in relazione al primo, poiché come l'essenza sta all'esistenza, così la verità sta alla credenza" (ibidem, 29 b-c). All'intelletto, il cui oggetto sono le forme intelligibili, si oppone dunque l'opinione vera, che ha per oggetto le cose sensibili percepite dal corpo; e a questa opposizione d'ordine epistemologico se ne aggiunge inoltre un'altra, di ordine sociologico: "si deve aggiungere che l'intelletto è proprio degli dèi e di un piccolo numero d'uomini" (ibidem, 51 e). Questo piccolo numero di uomini sono evidentemente i filosofi.
La scienza (epistḗmē) ha per oggetto la vera realtà, modello di ogni realtà sensibile e appresa non mediante i sensi, ma mediante l'intelletto (noũs). La conoscenza che ne risulta, e il discorso che trasmette tale conoscenza, sono contraddistinti dalla certezza, e riservati al filosofo. Per contro, l'opinione vera (alēthḗs dóxa) ha per oggetto le copie della vera realtà. Queste realtà derivate sono percepite dalla sensazione (aísthēsis) che, come si vedrà, risale per il tramite della reminiscenza fino alla specie razionale dell'anima e all'intelligibile. La conoscenza che risulta dalla sensazione non può tuttavia raggiungere la certezza, poiché ha per oggetto un'immagine mutevole. Lo stesso vale per il discorso che trasmette tale conoscenza, qualificato da Platone come "mito verosimile" (eikṓs mŷthos) o "discorso verosimile" (eikṓs lógos) proprio perché, dal momento che verte su immagini e non sulla vera realtà che ne costituisce il modello, non può essere vero nel pieno senso del termine.
Questo parallelismo tra realtà, conoscenza e discorso si trova illustrato, nella Repubblica, dall'allegoria della linea. La linea comporta due sezioni principali, delle quali l'una rappresenta quel che compete ai sensi, l'altra quel che compete all'intelletto: "Presa ora una linea divisa in due parti disuguali (se si accetta la lezione 'ánisa') dividi ancora ciascuna parte nella stessa proporzione, e cioè tanto la parte della specie visibile (horōménou) quanto quella della specie intelligibile (noouménou)" (Respublica, VI, 509 e). Il sensibile è designato, in qualche modo per sineddoche, come attinente soltanto alla vista: gli altri sensi (udito, gusto, olfatto e tatto) non sono nemmeno menzionati; d'altronde, l'intelletto è evocato soltanto mediante un verbo (noeĩn) che in Omero (Ilias, III, 374, 396; XV, 422; XXIV, 294) e in Esiodo (Theogonia, 878) designava la visione sensibile, come non manca di ricordare Aristotele nel De Anima (III, 3, 427 a 6 segg.). Platone si rivela erede di questa tradizione, poiché per lui oggetto dell'intelletto è la Forma, in greco eĩdos o 'idea' (termine che deriva da una radice - weid* che ha prodotto parecchi vocaboli relativi alla vista).
La descrizione della sezione inferiore della linea (Respublica, VI, 509 e - 510 a), quella che corrisponde al sensibile e che comprende due parti (una rappresentante le cose sensibili e l'altra le immagini di queste cose) introduce anch'essa alcune metafore visive. In entrambi i casi interviene la nozione di perspicuità, che si riferisce a realtà distinte soltanto per statuto ontologico: da un lato le cose sensibili e dall'altro le loro immagini. Mentre la parte più bassa della sezione inferiore ‒ immagini, riflessi, ecc. ‒ è descritta in modo esaustivo, l'altra parte non è oggetto di un inventario completo; sono considerati soltanto gli esseri viventi e i prodotti artigianali fabbricati dall'uomo. La sezione superiore della linea comporta, anch'essa, due parti: l'una corrispondente al dominio della matematica, l'altra a quello delle Idee, come dire delle forme intelligibili.
Platone non fa menzione dello statuto ontologico dei numeri e delle figure. Si limita a formulare due critiche: i geometri fanno uso di figure materiali e, soprattutto, restano al livello delle ipotesi (ibidem, 511 a-b). Il fatto che utilizzi immagini trascina la matematica verso il lato del sensibile; vi è però qualcosa di più grave. Il metodo deduttivo assume come punti di partenza presupposti, ipotesi, che considerati in sé non sono suscettibili di dimostrazione: come dunque dotarli di evidenza? L'evidenza ricercata non può essere discorsiva, poiché si trova all'origine ‒ e quindi al di fuori ‒ di qualsiasi deduzione; una tale evidenza non può che essere intuitiva e siccome non concerne il sensibile può essere prodotta soltanto da un'intuizione di ordine intelligibile. Di qui la necessità, dinanzi alla quale si trova Platone, di introdurre la dottrina delle Idee le quali, situandosi oltre i principî, ne garantiscono la validità.
Anche se non è possibile attribuire uno statuto specifico alle realtà matematiche o geometriche in quanto tali (ciascuna di esse ha tuttavia una Idea che le corrisponde: per es., quella del Due o quella del Cerchio), è giocoforza constatare il loro ruolo essenziale nella mediazione tra il sensibile e l'intelligibile. Lo studio della matematica consente dunque all'anima di risalire dal sensibile verso l'intelligibile e di assicurare la presenza dell'intelligibile nel sensibile.
Le Idee sono oggetto della dialettica, che per il tramite del processo di "riunione", risale dapprima di Idea in Idea verso il Bene, e poi, per il tramite del processo di "divisione", ridiscende di Idea in Idea per raggiungere una definizione, restando sempre nel dominio dell'intelligibile (ibidem, 511 b-c). La dialettica, così intesa, descrive dunque i rapporti tra le Idee e permette in qualche modo di stilare la mappa del mondo intelligibile. Essa presuppone però l'evidenza intuitiva, quella della ragione (noũs), che applicata alle Idee e infine al Bene serve da fondamento al processo deduttivo e garantisce la validità dei principî (che senza l'ipotesi dell'esistenza delle Idee resterebbero infondati).
La sezione relativa alla diánoia pone alcuni problemi, poiché sembra che nessuna realtà particolare corrisponda specificamente a questa facoltà cognitiva. Nella storia del platonismo sono state avanzate varie interpretazioni per attribuire un oggetto determinato alla diánoia: in particolare, si è ritenuto si trattasse del numero, con il quale veniva identificata l'anima, in quanto l'anima e il numero apparivano come due realtà intermediarie tra il sensibile e l'intelligibile. Ma, come si vedrà, tale identificazione sembra assai improbabile: da una parte perché la diánoia non è che una delle molteplici facoltà dell'anima, dall'altra perché, come l'anima, garantisce non soltanto l'influenza della matematica sulla realtà ma anche l'esistenza e la persistenza del movimento. Il dominio della diánoia, specie nella Repubblica, equivale a quello della deduzione, assimilato a un sistema formale nel quale, a partire da proposizioni considerate valide a priori, si cerca di dedurre un insieme di proposizioni vere, applicando alcune regole di inferenza non numerose e ammesse da tutti.
Le conoscenze
Il termine epistḗmē in Platone è riservato alla conoscenza della vera realtà, alla quale soltanto il filosofo può pervenire, e ciò lo rende simile alla divinità. La alēthḗs dóxa (opinione vera) non può che dar luogo a saperi specialistici: quei saperi cui diamo oggi il nome di 'scienze'. Platone in questo campo doveva essere debitore dei suoi predecessori: Democrito ed Empedocle per la fisica, ma anche Pitagora e i pitagorici per la matematica, e gli autori del Corpus Hippocraticum per la medicina. Tuttavia i problemi legati alla raccolta dei frammenti delle opere pervenuteci, alla loro classificazione e soprattutto alla loro interpretazione, rendono difficile una comparazione fruttuosa tra Platone e queste sue possibili fonti.
La matematica svolge un ruolo di primaria importanza in quanto presenta, come una moneta, due facce indissociabili, l'una orientata verso l'intelligibile, che essa permette di attingere, e l'altra orientata verso il sensibile, ove rappresenta le "tracce dell'intelligibile". Infatti essa permette di spiegare perché, a dispetto del cambiamento incessante al quale è soggetto, il sensibile dia adito a una conoscenza e a un discorso dotati di una certa universalità, di una certa permanenza. A questo livello, la matematica interviene in tutti i domini del sapere, come si cercherà di mostrare nonostante la difficoltà del compito: infatti, in greco, i diversi saperi sono sprovvisti di nomi specifici (a parte il caso dell'astronomia e della medicina), e ciò rende necessario l'uso, per indicarli, dei termini moderni; inoltre essi non sono né ben riconosciuti né accuratamente delimitati, non costituiscono un sistema, come accade invece oggi. Nel seguito dell'esposizione si dovrà dunque tenere conto di questo anacronismo, che è tuttavia ritenuto necessario in funzione dell'interpretazione proposta (che poggia peraltro su solide basi testuali).
La matematica
Dopo aver dimostrato, nella Repubblica (II, 372 d-IV, 427 c), la necessità di un gruppo di guerrieri, tra i quali selezionare quelli che diverranno filosofi e che dirigeranno la città, Socrate descrive a Glaucone il programma educativo che dovrà servire a formare tali filosofi: per formare i guerrieri, li si inizierà in primo luogo alla matematica, le cui differenti branche sono passate in rassegna. Il lungo passo che richiama la questione presenta questa particolarità: mentre Glaucone cerca di mettere in risalto ciò che, in ciascun caso, potrebbe presentare una concreta utilità per un guerriero, Socrate da parte sua insiste sul carattere astratto di ogni branca della matematica, anche se è pronto a riconoscere (525 b) che la matematica può essere utile ai guerrieri.
Come formare questi filosofi-dirigenti che dovranno distaccarsi dall'oscurità del sensibile per avanzare verso la luce dell'intelligibile? A tal fine non è possibile affidarsi all'educazione tradizionale basata sulla ginnastica e sulla musica (intesa in senso lato come tutto quel che compete alle Muse). La ginnastica è evidentemente incapace di sfuggire al sensibile, dato che si interessa prioritariamente al corpo; lo stesso vale per la musica, ove si consideri che l'armonia e il ritmo si rapportano all'udito, e sono solitamente imposte dall'esterno tramite l'abitudine. Le altre arti sono già state rigettate in quanto meccaniche (VI, 495 d); è dunque soltanto con l'aritmetica (522 c-526 c) che si comincia ad apprendere qualcosa di superiore al sensibile.
Ogni percezione sensibile ha come effetto di suscitare la percezione sensibile del suo opposto. E la mente non può avere coscienza dell'unità e della pluralità che risiede nella diversità, prima che la sensazione le abbia fornito informazioni sugli attributi contrari dello stesso oggetto.
Anche se questa coscienza dell'unità resta rudimentale, si tratta di un atto di pura intellezione, un atto che, quando sia suscitato in noi dallo studio del numero, diviene un incomparabile strumento di risveglio del pensiero. L'aritmetica costituisce dunque il primo passo verso un'educazione superiore. Anche la geometria è assolutamente indispensabile per accedere a un'educazione superiore (526 c-527 c): difatti, pur se celato dall'uso di un nome che richiama un'applicazione pratica ‒ quella di misurare (‹metria›, da métron, misura) la Terra (‹geō›, da gẽ, terra) ‒ il suo vero scopo, almeno nell'opinione di Socrate, è quello di pervenire a risultati astratti, universali, e anche, si può dire, eterni. Inoltre, secondo Platone, l'esperienza dimostra che se l'aritmetica rende la mente più agile, la geometria la educa.
Socrate fa osservare che vi è una branca della geometria, molto trascurata, cui si dovrebbe attribuire un rango primario. La geometria è infatti generalmente intesa come geometria piana, ma si deve altresì considerare la geometria dello spazio a tre dimensioni: la geometria dei solidi, ovvero la stereometria (527 d-528 e). È questa infatti a essere richiesta nell'astronomia, quale scienza di solidi in movimento. Sebbene si trovi sempre "nella sua infanzia", questa scienza intermediaria necessita di essere approfondita, ma essa è talmente difficile che il suo sviluppo dipende esclusivamente dal fascino che è in grado si esercitare sulle menti.
Per quanto riguarda la geometria dei corpi in movimento, quella che, come or ora ricordato, interessa l'astronomia (529 a-530 c), mentre Glaucone loda la contemplazione del cielo stellato per la sua sola utilità pratica e non come modo di elevarsi dal sensibile all'intelligibile, Socrate replica che la mente può guardare in basso anche se lo sguardo è rivolto in alto, se essa si accontenta di osservare senza cercare di elevarsi verso le verità universali. Il cielo appare come un immenso quadro in movimento. Tuttavia, proprio come la geometria, l'astronomia deve andare oltre i fenomeni per determinare i principî generali che reggono il movimento dei solidi; essa deve dunque lasciare da parte la contemplazione del cielo per interessarsi ai veri problemi, che sono di ordine matematico.
La teoria della musica, infine (un sapere che, in un primo tempo, non presenta nulla di evidente per Glaucone), può essere elevata non soltanto al disopra delle dispute tra musicisti, ma anche oltre i limiti a essa imposti dai pitagorici, che non si interessavano ad altro se non alle armonie percepibili con l'udito. Coloro che vogliono diventare filosofi devono elevarsi verso la contemplazione universale e astratta dei rapporti armonici in sé ‒ come si constata nel Timeo ‒ i quali rapporti spiegano la regolarità dei movimenti dei corpi celesti che non emettono alcun suono; di qui l'importanza dell'armonica (530 c-531 c).
Così svincolati dall'empirismo, tutti questi saperi matematici sono portati a un livello che rende possibile considerarli in correlazione gli uni con gli altri; allora possono veramente diventare il preludio (ma non più di questo) alla dialettica, lo studio delle vere realtà da parte del puro pensiero. Soltanto la ragione, pur usando le ipotesi nel quadro dei saperi specialistici, può oltrepassarle e separarsene; dunque non è la diánoia, ma la dialettica che può apprendere le Idee e giungere al Bene. Le Idee, che costituiscono la vera realtà, non sono sensibili, e non dipendono da principî superiori. Per Platone la scienza (epistḗmē), vale a dire la dialettica intesa nel senso che riveste nella Repubblica, perviene alla certezza perché conduce alla contemplazione di Idee che rappresentano la vera realtà, colta in un atto d'intuizione puramente intellettuale.
Cosmologia
Platone nel Timeo sviluppa una cosmologia proponendo una rappresentazione semplice, ma coerente e rigorosa, dell'Universo, le cui proprietà appaiono come conseguenze, logicamente dedotte, di un limitato insieme di presupposti (anche se in questo dialogo essi restano impliciti o mal esplicitati). Il Timeo appare, inoltre, come la prima cosmologia in cui la descrizione dell'Universo è condotta con l'ausilio della matematica, e non solamente del linguaggio ordinario (come sarà il caso di Aristotele che, specie nel De caelo e nella Fisica, non cesserà di criticare questa matematizzazione dell'Universo intrapresa da Platone). Tuttavia, ed è qui che il Timeo si àncora nella tradizione attraverso un mito, la descrizione dell'Universo in Platone resta indissociabile da una descrizione dell'origine dell'uomo e anche dell'origine della società, come illustra il mito di Atlantide, riassunto all'inizio del dialogo e narrato nel Crizia.
Per Platone una cosmologia che intenda proporre una rappresentazione semplice dell'Universo deve essere in grado di dare risposta a due domande: a quali condizioni il mondo sensibile può divenire intelligibile? Come riuscire a descriverlo? Queste domande sorgono dalla convinzione che il cambiamento incessante non può essere considerato come la vera realtà, e che, per divenire oggetto di conoscenza e di discorso, il mondo sensibile deve presentare, nel suo stesso mutamento, qualche cosa che non cambi, qualche cosa che presenti una vera permanenza e che dunque si ritrovi, in tutti i casi, identico. L'ipotesi dell'esistenza di forme intelligibili ‒ le Idee ‒ comporta due problemi specifici: quello della partecipazione delle Idee tra di loro, e quello della partecipazione delle forme sensibili alle forme intelligibili. Questi problemi sono esposti nel Parmenide; per risolvere il primo è proposta una soluzione nel Sofista e, per rispondere al secondo, Platone avanza, nel Timeo, due ipotesi: quella di un demiurgo, che fabbrica o, piuttosto, ordina l'Universo; e quella della chṓra, il materiale sul quale il demiurgo interviene. Nella misura in cui la somiglianza può essere definita come un'identità ridotta a certi aspetti, le cose sensibili ‒ in quanto mere immagini delle forme intelligibili ‒ devono presentare un certa somiglianza con esse e al tempo stesso differirne; il demiurgo garantisce la somiglianza, mentre la chṓra spiega la differenza.
Un certo numero di predicati, positivi e negativi, permette di descrivere la natura del demiurgo: poiché è un dio ‒ e un dio per Platone deve essere buono (cfr. Respublica, II) ‒ il demiurgo è buono (Timaeus, 29 e) e, in quanto tale, l'intelletto dirige la sua azione, dato che in Platone la bontà è legata alla razionalità. Questa razionalità si manifesta nel calcolo e nella parola, e si realizza in un lavoro tecnico simile a quello di vari artigiani; questi due tratti indicano il duplice aspetto del Timeo, meccanicistico e intenzionale. Per realizzare il suo scopo, il demiurgo si mette al lavoro contemplando un modello per trasformare un materiale, obbedendo a un certo numero di regole e realizzando certi obiettivi. In questa metafora artigianale è in gioco tutto il Timeo: il demiurgo, poiché è buono, è sprovvisto di "gelosia" (in greco, phthónos è un termine che designa questa paura di vedere qualcun altro uguagliarci o superarci nella potenza o in qualsiasi altra qualità), e intraprende la costruzione di un mondo che sia il più bello possibile. Egli però ‒ come ogni altro artigiano ‒ non è onnipotente, e questo per due motivi: l'esistenza delle forme intelligibili e quella della chṓra non dipendono da lui; inoltre, la chṓra (che traduciamo con "materiale" per evitare il termine aristotelico "materia"), su cui egli interviene, resiste passivamente ai suoi sforzi.
Tre esigenze, d'altronde, portano ad avanzare l'ipotesi della chṓra:
1) essa spiega perché le cose sensibili sono diverse dalle forme intelligibili, delle quali peraltro partecipano (ibidem, 52 c-d);
2) la chṓra è ciò che fornisce una collocazione alle cose sensibili ed è un ricettacolo stabile nel quale le cose sensibili compaiono e, dopo un certo tempo, scompaiono;
3) infine, essa presenta, per le cose sensibili, un aspetto costitutivo (e ciò Platone lo lascia capire utilizzando un certo numero di immagini e di metafore relative soprattutto alla madre e alla nutrice).
La chṓra comporta, dunque, un doppio aspetto, spaziale e costitutivo; in sé stessa, è sprovvista di misura e di proporzione e, di rimando, può ammettere ogni specie di misura e di proporzione. Nel Timeo essa non è mai descritta in quanto tale, allo stato puro; quando il demiurgo decide d'introdurvi misura e proporzione, essa già presenta le tracce dei quattro elementi (ibidem, 52 d-53 c), agitati da un moto automatico e in qualche modo meccanico, sprovvisto di ordine e misura (v. oltre). Questo principio di resistenza è chiamato da Platone anánkē, termine che si traduce di solito con "necessità", ma che deve essere compreso come l'insieme delle conseguenze ineluttabili che nel mondo sensibile impongono limiti severi a ogni intento razionale. Ammettendo la persistente presenza della necessità nell'Universo, con la quale prima il demiurgo e poi l'anima del mondo (v. oltre) devono fare i conti, Platone riconosce che l'ordine presupposto dal suo modello cosmologico è costretto a restare parziale e provvisorio; ne segue che anche ogni spiegazione cosmologica è condannata a restare parziale e provvisoria.
Nel mondo sensibile la permanenza si manifesta con questi aspetti: causalità, stabilità e simmetria. Vi è causalità se ogni effetto dipende da una causa; stabilità, se la stessa causa produce sempre lo stesso effetto; simmetria, se questo rapporto di causalità resta invariato nonostante le incessanti trasformazioni. Questa invarianza, che può essere espressa in termini di rapporti matematici, costituisce di fatto l'essenziale di quel che l'uomo perviene a conoscere e a descrivere del mondo sensibile. Comunque, la conoscenza e il discorso che hanno come oggetto le cose sensibili non sono mai veri, restano verosimili, in quanto vertono su immagini e non sulla vera realtà.
Il demiurgo, con lo sguardo fisso sulle forme intelligibili, fabbrica l'Universo quale un essere vivente, dotato di un'anima e di un corpo. Il corpo del mondo ha l'aspetto di una gigantesca sfera, dato che ‒ come copia di un originale perfetto ‒ deve avere la forma più perfetta, più simmetrica, e nella geometria dello spazio a tre dimensioni, nessuna forma è più simmetrica della sfera.
Astronomia
Perché Platone considera l'Universo come un essere vivente, vale a dire come un essere dotato di anima? S'è visto che il problema principale della sua cosmologia consiste nello spiegare ciò che nel mondo sensibile, il quale non cessa di mutare, è stabile e ordinato, e spiegare ‒ soprattutto ‒ i movimenti più regolari che vi si osservino, quelli dei corpi celesti. Ma come spiegare l'origine di questi movimenti e la causa dell'ordine che essi manifestano? Per rendere conto dell'origine e della persistenza dell'insieme dei movimenti nell'Universo ‒ e soprattutto dei più nobili, quelli che animano i corpi celesti ‒ Platone formula l'ipotesi d'una realtà che i sensi non percepiscono: l'anima del mondo.
Negli esseri viventi ‒ provvisti, per definizione, di questo principio di movimento spontaneo che Platone chiama "anima" ‒ si manifesta, nel cambiamento, una certa regolarità: tale specie genera tale specie, vive quel certo numero di anni, presenta tali caratteristiche, ecc. Di più, l'anima dell'uomo è dotata di un intelletto, che gli assicura una condotta coerente e conforme a certe intenzioni, più o meno ben definite. Un ragionamento analogico permette di comparare queste due serie di fatti e di supporre che il mondo sensibile si trovi provvisto di un'anima dotata di ragione (Timaeus, 30 a-c), come nel caso dell'uomo; alla luce di questo presupposto, il demiurgo inizia a fabbricare il corpo e l'anima di un vivente che racchiude tutti i viventi, e cioè l'Universo. L'anima del mondo, che conserva nell'Universo l'ordine instaurato dal demiurgo (ibidem, 34 c), possiede le seguenti caratteristiche: è una realtà intermedia, presenta l'aspetto di un intreccio di circonferenze (la più "nobile" tra le figure piane, in quanto dotata della più grande simmetria), che intrattengono tra di loro dei rapporti matematici e, infine, spiega ogni movimento, sia psichico sia fisico, nell'Universo.
Nel Timeo, la descrizione della costituzione dell'anima del mondo presenta la forma di un racconto che si svolge nel tempo. Procedendo in tal modo, Platone non viola il postulato formulato nel Fedro (245 c-246 a) sul carattere ingenerato di ogni principio, e specialmente di quel principio di movimento ordinato che è l'anima; difatti la "fabbricazione" dell'anima del mondo da parte del demiurgo non implica un'origine nel tempo.
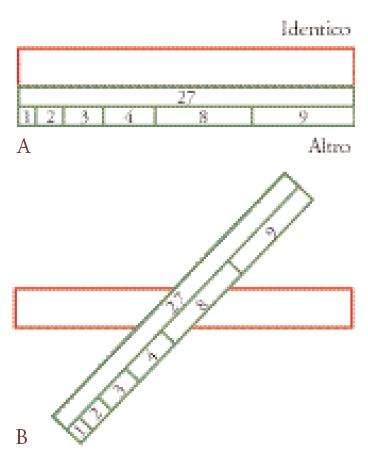
Nella descrizione delle mescolanze effettuate dal demiurgo per fabbricare l'anima del mondo (tab. 1; Timaeus, 35 a-b), dapprima intervengono i termini più generali dell'ontologia platonica: l'Essere, l'Identico e l'Altro, i grandi generi evocati nel Sofista (254 d-259 b). L'anima comporta infatti le stesse caratteristiche essenziali di ogni altra realtà: l'essere (x esiste), l'identità (x è x, è quel che è) e l'alterità (x è differente da tutto ciò che non è x, dunque non è y, z, ecc.). Questa descrizione si limita a illustrare due cose: da una parte la dipendenza ontologica dell'anima del mondo rispetto al mondo delle Idee, e dall'altra il suo statuto di realtà intermedia tra questo mondo e quello delle cose sensibili. Questa realtà intermedia rappresenta, nel sensibile, l'origine di ogni movimento ordinato, i movimenti circolari dei corpi celesti e i movimenti rettilinei delle realtà sublunari. Di qui il fatto che il Timeo presenti la costituzione dell'anima del mondo come se si trattasse della fabbricazione di una sfera armillare, ovvero di un globo formato da anelli o cerchi rappresentanti il movimento del cielo e degli astri (evocata in Timaeus, 40 d).
Dopo aver realizzato la mescolanza fondamentale che serve a fabbricare l'anima del mondo, il demiurgo, che lavora come un fabbro, lamina questa massa per trasformarla in una placca in cui introduce un certo numero di divisioni. Egli inizia con il dividerla in senso longitudinale (v. fig. 2A) per ottenere due strisce, che chiama la banda dell'"Identico" e quella dell'"Altro" (anche se ciascuna di esse è costituita da una mescolanza di Essere, di Identico e di Altro). L'operazione tecnica così realizzata dal demiurgo spiega, su un piano metaforico, la distinzione osservata tra le stelle fisse, che si muovono da est a ovest e i pianeti, che vanno da ovest a est: proprio come l'Identico e l'Altro sono due contrari, così i corpi celesti che si muovono sul cerchio dell'Identico (le stelle fisse) e su quello dell'Altro (i pianeti) vanno in direzione opposta. Queste bande rendono possibile la fabbricazione dei due cerchi sui quali si muoveranno i corpi celesti (la permanenza è assicurata, in uno spazio a due dimensioni, dalla perfetta simmetria del cerchio). Il demiurgo prosegue poi il suo lavoro ripartendo la banda dell'Altro in sette sezioni, che permetteranno di fabbricare i cerchi sui quali si sposteranno sette astri (il Sole, la Luna, e i cinque pianeti allora conosciuti).
Tuttavia, non basta dar conto della permanenza dei movimenti dei corpi celesti: si deve altresì dar conto della loro regolarità. È qui che interviene la 'medietà' (il sostantivo, dal greco mesótēs, nel contesto in cui ora si situa Platone designa sia un insieme di tre termini (A, B, C) sia il termine medio di questa progressione, ovvero B). La teoria delle 'medietà' s'inscrive a priori nel quadro dell'aritmetica e delle sue applicazioni alla musica: A, B e C designano allora dei numeri. Intercalare un medio B tra A e C, significa dividere il rapporto A:C in due rapporti A:B e B:C, di cui si compone A:C. Sono introdotti tre tipi di medietà, che corrispondono alla costruzione delle medie geometrica, aritmetica, armonica (v. tab. 2). Queste erano già adoperate da Pitagora, secondo Giamblico (In Nicomachi arithmeticam introductionem, 100, 19) ma, trattandosi di una testimonianza tardiva, il giudizio sulla sua validità deve essere prudente.
Il demiurgo divide la banda dell'Altro secondo gli intervalli dati da una successione di sette numeri: 1, 2, 3, 4, 9, 8, 27, ottenuti fondendo due progressioni geometriche (vale a dire, ogni numero è la media geometrica del precedente e del conseguente): la prima 1, 2, 4, 8 (che produce intervalli doppi, vale a dire la distanza fra due numeri consecutivi è due), e la seconda 1, 3, 9, 27 (che produce intervalli tripli) (tab. 2). Di seguito, operando separatamente su ognuna delle due progressioni, il demiurgo inserisce altri numeri fra questi sette: in ogni intervallo due termini medi che sono delle medietà armoniche e delle medietà aritmetiche.
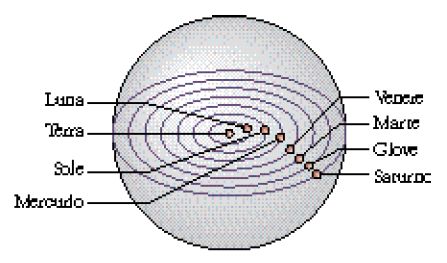
Si arriva così a due successioni di dieci numeri: nella prima (intervalli doppi) il rapporto fra due termini consecutivi è, alternativamente, 4/3 e 9/8 e nella seconda (intervalli tripli) 4/3 e 3/2. Benché questa descrizione presenti alcuni punti poco chiari, essa risponde a considerazioni tecniche assai chiare. Le proporzioni descritte si applicano a una serie di numeri interi positivi che rappresentano i raggi dell'orbita di ciascuno dei sette pianeti attorno alla Terra: Luna, Sole, Mercurio, Venere, Marte, Giove, Saturno.
L'introduzione di 'medietà' nell'anima del mondo, che può sembrare sconcertante, si inserisce in realtà nel contesto di un ragionamento analogico: Platone sembra voler mettere al servizio dell'astronomia l'armonica sviluppata a partire dalla scoperta dell'armonia musicale. Applicando gli stessi rapporti matematici a oggetti materiali, all'occorrenza a corde di misure differenti, si arriva a produrre dei suoni, sempre gli stessi, i quali costituiscono un'armonia che non ha invero più nulla di materiale; in altri termini, con l'aiuto di rapporti matematici che appartengono unicamente alla ragione, si perviene a spiegare i suoni musicali, e persino a produrli, nel mondo sensibile. Perché allora non dovrebbe essere lo stesso in astronomia, tanto più che i movimenti dei corpi celesti presentano una regolarità e una permanenza che fin dalla più remota antichità hanno stupito gli esseri umani, al punto di farli assimilare a divinità? Per rendere conto di queste due caratteristiche, permanenza e stabilità, egli formula due postulati: (1) i movimenti dei corpi celesti seguono una traiettoria circolare, il loro movimento è dunque permanente; (2) questi movimenti obbediscono a leggi definite da tre tipi di relazione matematica conosciuti all'epoca, il loro movimento è dunque regolare, a dispetto delle apparenze.
Da un punto di vista strettamente musicale, la struttura matematica dell'anima del mondo comprenderebbe quattro ottave, una quinta e un tono: 2/1×2/1×2/1×2/1×3/2×9/8=17; Platone, tuttavia, si rifiuta esplicitamente di teorizzare quale tipo di musica potrebbero emettere i corpi celesti, il cui moto non produce alcun rumore (Timaeus, 37 b).
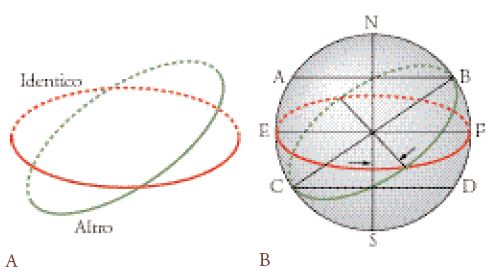
Il demiurgo, dopo aver separato in due parti la placca descritta precedentemente, fa coincidere nel mezzo le bande così ottenute, secondo la figura della lettera greca χ (fig. 2B). Egli curva poi le due bande in cerchio e ne salda le estremità, costituendo così due cerchi (quello dell'Identico e quello dell'Altro) inclinati l'uno rispetto all'altro (fig. 3A): il primo, quello 'dell'Identico', trasporta da ovest a est l'insieme della sfera in cui consiste il mondo sensibile, oltre alle stelle fisse, mentre il secondo, quello 'dell'Altro', come si è detto, trasporta i sette pianeti noti all'epoca (fig. 3B). Infine, il demiurgo passa all'ultima operazione, che consiste nel suddividere per sei volte la rivoluzione del cerchio interno (Timaeus, 36 d), per ottenere sette cerchi diseguali corrispondenti alle orbite dei pianeti, mentre la Terra resta immobile al centro del mondo sensibile (ibidem, 40 b-c) (fig. 4).
Platone perviene dunque a proporre un sistema astronomico di stupefacente semplicità (ibidem, 38 c - 39 e). Questo sistema fa intervenire infatti soltanto il movimento circolare ‒ ipotesi che sussisterà fino a Keplero (legge delle orbite, 1609) ‒ e prende in considerazione i tre tipi di rapporti di medietà (geometrica, aritmetica e armonica) della tab. 2.
Il sistema astronomico di Platone considera anzitutto il moto, sia esterno sia interno, dell'Universo e delle stelle fisse. Il 'moto esterno' dell'Universo, che si svolge da sinistra a destra, da ovest a est ed è indicato come il movimento dell'Identico, comunica una rotazione assiale alla totalità della sfera in cui consiste il corpo del mondo. Il 'moto interno' dell'Universo, che si svolge da destra a sinistra, da est a ovest ed è inclinato sul piano dell'eclittica, è considerato come un movimento dell'Altro che coinvolge ciascuno dei sette pianeti (la Luna, il Sole e i cinque pianeti allora conosciuti, ossia Mercurio, Venere, Marte, Giove, Saturno); è da osservare che questo movimento è dominato da quello dell'Identico, il che spiega come la sfera del mondo ruoti sempre nello stesso verso. Quanto al moto delle stelle fisse, l'Identico comunica a ciascuna di esse un movimento in avanti, che corrisponde alla rivoluzione quotidiana della stella sulla volta celeste, e una rotazione assiale, la quale ultima è dovuta all'azione dell'anima del mondo.
Come detto poco sopra, la Terra è immobile al centro dell'Universo (fig. 4), in quanto il movimento di rotazione assiale della sfera del mondo dovuto all'Identico, al quale essa partecipa, è compensato da un opposto movimento di rotazione assiale di cui essa è dotata. Passando ai pianeti, l'Identico e l'Altro comunicano ciascuno il proprio movimento a ogni pianeta, che si muove su una delle sette parti in cui è stata divisa la banda dell'Altro; il moto prevalente è quello dell'Identico, per cui il moto risultante di ciascuno dei pianeti suscita l'impressione di una torsione a spirale; in gruppo, i pianeti hanno una velocità uguale a quella del cerchio dell'Altro e, a parte la Luna e il Sole, presentano retrogradazioni. In particolare: il movimento della Luna è accelerato rispetto a quello dell'Altro; il movimento del Sole è quello stesso dell'Altro; Mercurio e Venere presentano retrogradazioni intermittenti che alterano il loro movimento rispetto a quello dell'Altro; Marte, Giove e Saturno sono più lenti dell'Altro in quanto presentano retrogradazioni che li trascinano in verso contrario a quello degli altri quattro pianeti.
La straordinaria complessità dei movimenti che apparentemente interessano i corpi celesti è così dominata grazie a due elementi d'ordine matematico: il cerchio e la 'medietà'. Sono d'altronde questi due elementi che permettono di costruire un modello meccanico relativamente semplice, che aiuta l'astronomo a illustrare le sue conclusioni. Rapidamente, però, ci si rese conto, anche nell'ambito dell'Accademia, che una spiegazione così semplicistica non era in grado di rendere conto di tutti i fenomeni celesti.
La dottrina degli elementi
Il demiurgo adatta l'anima del mondo, così fabbricata, al corpo del mondo (Timaeus, 34 b, 36 d-e). Conformandosi a una tradizione che probabilmente risale a Empedocle, Platone dà per scontato, che il corpo dell'Universo sia stato costruito esclusivamente a partire da quattro elementi: fuoco, aria, acqua e terra (56 b-c). Ma va molto più lontano; avanza infatti un argomento matematico per giustificare il fatto che vi debbano essere quattro elementi e, soprattutto, è consapevole di introdurre un'importante novità (53-e) stabilendo una corrispondenza tra i quattro elementi e quattro poliedri regolari, vale a dire trasponendo in termini matematici la realtà fisica nella sua globalità e i mutamenti che la riguardano. La costruzione dei primi poliedri regolari è attribuita a Teeteto (m. nel 369 o 368 a.C.), un contemporaneo di Socrate, che Platone fa comparire nel prologo di un dialogo che porta il suo nome: ciò dimostra quanto egli fosse attento allo sviluppo della matematica del suo tempo. Platone nel Timeo (31 b-32 b) esamina dapprima il caso in cui il mondo presenti soltanto due dimensioni; in tale mondo piatto sarebbero sufficienti tre elementi. Il motivo risiede nel fatto che tra due numeri quadrati esiste soltanto un termine medio; usando la notazione moderna, dati due numeri a², b², il termine medio proporzionale è x=ab, in quanto a²/ab=ab/b²: per esempio, fra 4 (2²) e 9 (3²), il detto termine è 6=2×3. Ma il nostro è un mondo a tre dimensioni. Ora, fra due numeri 'cubici', per esempio 8 (2³) e 27 (3³), si trovano due termini medi, 12 (2²×3) e 18 (2×3²), ciò che può esprimersi così: dati due numeri cubici a³, b³, i termini medi sono a²b e ab² in quanto a³/a²b=a²b/ab²=ab²/b³. Poiché l'Universo nel quale viviamo presenta tre dimensioni, deve comportare anche quattro elementi. Per arrivare a scoprire questi due termini medi s'imponeva però l'uso della radice quadrata (e della radice cubica); poiché il problema della costruzione geometrica di tali quantità all'epoca non era ancora risolto, si comprende immediatamente perché, qualche riga oltre, Platone scriva che il demiurgo "ponesse acqua e aria tra fuoco e terra e in rapporto proporzionale per quanto era possibile" (ibidem, 32 b).
I quattro elementi di cui è fatto il nostro Universo (la terra, l'acqua, l'aria e il fuoco) sono interpretati matematicamente associando il fuoco al tetraedro, l'aria all'ottaedro, l'acqua all'icosaedro e la terra al cubo. Il demiurgo dunque ha fabbricato il corpo del mondo a partire da corpi geometrici perfetti, la sfera e i poliedri regolari; e i movimenti e le interazioni dei poliedri sono governati da leggi matematiche, almeno laddove l'anánkē si è voluta piegare a essi.
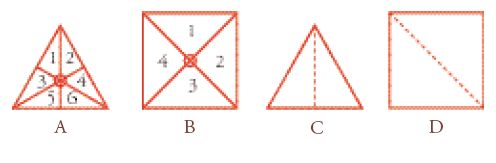
La costituzione degli elementi. I quattro poliedri degli elementi sono costruiti a partire da due tipi di superfici piane, il quadrato e il triangolo equilatero, che a loro volta risultano da due tipi di triangoli rettangoli, ossia il triangolo rettangolo isoscele e il triangolo rettangolo scaleno. Un triangolo equilatero risulta dall'unione di sei triangoli rettangoli scaleni (54 d-e) (fig. 5A) e un quadrato risulta dall'unione di quattro triangoli rettangoli isosceli (55 b) (fig. 5B); per costituire un triangolo equilatero sarebbero stati sufficienti due triangoli rettangoli scaleni (fig. 5C) e due triangoli rettangoli isosceli per un quadrato (fig. 5D). Si può tuttavia pensare che nel caso del quadrato e in quello del triangolo equilatero Platone voglia trovare un centro di simmetria (cfr. Euclide, Elementa, XIII, 18, scolio) tale da far sì che nessuno dei triangoli costitutivi del quadrato o del triangolo equilatero possa avere una preminenza sugli altri. Potrebbe trattarsi di una critica implicita al pitagorismo, ove alla sinistra e alla destra era attribuito valore opposto.
Come mostra la tab. 3, i triangoli equilateri servono a costruire il tetraedro (ibidem, 54 e-55 a: 4 triangoli equilateri), l'ottaedro (55 a: 8 triangoli equilateri) e l'icosaedro (55 a-b: 20 triangoli equilateri), associati rispettivamente al fuoco, all'aria e all'acqua, mentre i quadrati servono a costituire il cubo (55 b-c: 6 quadrati), associato alla terra. Infine si trova, citato di sfuggita, il dodecaedro, il poliedro regolare più vicino alla sfera (55 c), figura geometrica alla quale è associato il corpo del mondo (cfr. Epistula XIII [apocrifa] 363 d).
I poliedri regolari che corrispondono ai diversi elementi sono pertanto descritti esclusivamente in funzione del numero di facce che compongono i loro involucri. La lunghezza degli spigoli dei poliedri può essere ottenuta a partire dalla lunghezza dell'ipotenusa dei triangoli rettangoli elementari che compongono le facce. Ora, questo valore resta indeterminato (ibidem, 57 c-d) e tale indeterminazione è di notevole importanza per due motivi: se da un lato riduce il potere esplicativo del modello geometrico proposto da Platone opponendosi alla sua semplicità, d'altro lato essa permette di rendere meglio conto delle varietà di uno stesso elemento.
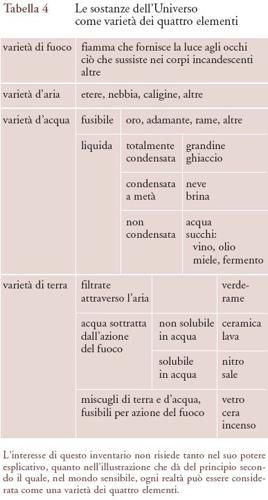
Platone vuole infatti mostrare come il modello cosmologico che propone consenta di descrivere gli oggetti del mondo sensibile i quali sono varietà dei quattro elementi, o loro combinazioni, nonché le loro proprietà. Le sostanze più complesse che si trovano nell'Universo non sono altro, in definitiva, che varietà di quattro ‒ e soltanto quattro ‒ elementi (58 c-61 c), peraltro associati a quattro poliedri regolari, a loro volta costituiti di due tipi di triangoli rettangoli ai quali, in ultima istanza, è ricondotta tutta la struttura materiale dell'Universo (v. tab. 4).
Le corrispondenze stabilite tra il numero dei triangoli equilateri che compongono la superficie dei poliedri permettono, inoltre, di formulare le equivalenze matematiche che spiegano come i quattro elementi si trasformino gli uni negli altri, e come si producano i fenomeni di generazione e di corruzione che si manifestano nel mondo sensibile. Una tale spiegazione si basa sul seguente presupposto: i due tipi di triangoli rettangoli elementari non possono essere né creati, né distrutti; di conseguenza, il numero di triangoli di ogni specie implicata in una trasformazione è conservato. Inoltre, possono trasformarsi gli uni negli altri soltanto gli elementi che corrispondono a poliedri le cui facce siano formate da triangoli equilateri. Ne consegue che l'acqua, l'aria e il fuoco possono trasformarsi gli uni negli altri (ma non così la terra, che corrisponde al cubo, le cui facce sono dei quadrati) e sono i soli interessati da processi di decomposizione e di ricomposizione. In breve, la trasformazione degli elementi è considerata in funzione dei triangoli equilateri (△) che compongono i poliedri regolari, e non, come sarebbe naturale, in funzione dei volumi (v. tab. 5). Questo tipo di soluzione sorprende, poiché considera soltanto le superfici che limitano i poliedri, mentre i poliedri sono dei volumi. Bisogna ricordare però che, come si constata ancora in Euclide, quello che definisce un poliedro è la sua forma, ovvero il suo limite, che corrisponde all'insieme delle sue facce. D'altra parte, l'indeterminazione della lunghezza dell'ipotenusa dei triangoli rettangoli elementari che compongono i triangoli equilateri rende difficile la spiegazione della mutua trasformazione di quei poliedri le cui facce non siano costituite da triangoli equilateri di identica superficie. Infine, la matematica del tempo di Platone incontrava notevoli difficoltà per estrarre le radici quadrate e si trovava nell'impossibilità di estrarre le radici cubiche.
Irrazionalità e incommensurabilità. L'estrazione delle radici quadrate conduce molto rapidamente al problema delle grandezze incommensurabili con l'unità, problema che è evocato nel Teeteto (147 c-148 d). Il testo di questo passo si divide in due parti. In una prima parte, assai breve, Platone rievoca l'insegnamento di Teodoro di Cirene (seconda metà V sec. a.C.) e, soprattutto, la lezione di recente impartita ad Atene a un gruppo di giovani di cui facevano parte Teeteto e un giovane omonimo di Socrate. La seconda parte sviluppa una definizione limitata dell'irrazionalità a partire da una classificazione dei numeri interi che distingue i quadrati perfetti e gli altri numeri, così come i cubi perfetti e gli altri numeri. Teodoro affronta il problema dell'incommensurabilità sia utilizzando un procedimento (aritmetico) di calcolo, sia ricorrendo all'antiferesi (Euclide, Elementa, lib. VII, prop. 1 e 2, e lib. I) o antaneresi (Aristotele, Topica, VIII, 3, 158 b 29-159 a 1), procedimento (geometrico) di approssimazione di grandezze per sottrazioni successive e alternate; di qui l'elogio rivoltogli da Socrate, che lo qualifica come "l'uomo più forte nei calcoli e più profondo conoscitore della geometria" (Politicus, 257 a 6-8). Teodoro prova per la prima volta ‒ anche se in modo incompleto e facendo ricorso all'induzione ‒ l'esistenza geometrica di segmenti incommensurabili con l'unità, corrispondenti alle radici quadrate di numeri che non sono quadrati perfetti. L'equivalenza tra la non esistenza aritmetica di un rapporto e l'esistenza geometrica di segmenti corrispondenti era a quel tempo stabilita per (2)¹/², come si constata leggendo il Menone (81 a-84 b), e forse per altri numeri. Teodoro non ritorna su questo particolare problema, ma mostra che l'equivalenza tra la non esistenza aritmetica di un rapporto e l'esistenza geometrica di segmenti corrispondenti può essere stabilita per altri numeri, fino a 17 o 19 (secondo le interpretazioni).
Quale che sia il ruolo dell'espediente narrativo di Platone, una cosa resta chiara: in un dialogo consacrato alla scienza, sono rievocate alcune opere che provano l'esistenza geometrica di vari irrazionali quadratici. Ciò che poteva essere considerato come un'eccezione è riconosciuto come il caso più frequente. In un primo tempo, è stabilita una distinzione tra i numeri esprimibili come prodotti di due fattori uguali (vale a dire n=a×a) e quelli che non lo sono. Per i numeri solidi, cioè esprimibili come prodotto di tre numeri, Teeteto stabilisce un'analoga distinzione tra i numeri che possono essere espressi come prodotti di tre fattori uguali n=a×a×a (numeri cubici), e quelli che non possono esserlo. E, nel caso di tutti i numeri che non sono dei cubi perfetti, ossia n=a²b, n=ab² e n=abc, compresi i numeri primi (che hanno la forma n=a×1×1) se esprimono il volume di un cubo, lo spigolo del solido corrispondente ha una misura irrazionale.
I limiti appena descritti sono reali e attenuano l'interesse del modello cosmologico platonico. Ciò non toglie che il demiurgo abbia fabbricato l'Universo a partire dai corpi geometrici più perfetti, la sfera e i quattro poliedri regolari; che i movimenti e le interazioni di tali poliedri regolari siano governati da leggi matematiche (beninteso, soltanto laddove l'anánkē sia stata persuasa a sottomettersi a quest'ordine); e dunque che il corpo dell'Universo sia il più perfetto possibile, allo stato attuale delle cose.
Il problema del movimento. L'ipotesi dell'anima del mondo permette a Platone di spiegare non soltanto perché e come sia ordinato il movimento dei corpi celesti (v. sopra), ma anche come e perché il movimento dei corpi sublunari sia anch'esso soggetto a leggi matematiche; in tal modo si spiega come il movimento presenti una certa regolarità e una certa permanenza. Più l'anima del mondo sarà regolata da leggi matematiche rigorose, più i movimenti che il mondo sensibile presenta avranno la possibilità di essere ordinati.
Per rendere conto dei cambiamenti che riguardano l'insieme del mondo sensibile è necessario introdurre tre principî. In primo luogo, l'Universo non è uniforme, e il movimento che vi si osserva trae la sua origine dalla non uniformità che vi regna (Timaeus, 57 e). Questa non uniformità può spiegarsi in due modi: un'interpretazione debole la giustifica con il fatto che esistono quattro poliedri regolari che non possono esattamente incastrarsi gli uni negli altri; un'altra, più forte, vuole che essa risulti dal fatto che la lunghezza dell'ipotenusa dei triangoli rettangoli elementari resta indeterminata, e ne segue che le dimensioni dei poliedri elementari che compongono tutte le cose sensibili possono differire. Questa assenza di uniformità costituisce dunque la causa del cambiamento incessante cui è soggetto il mondo sensibile, un cambiamento che l'anima del mondo tenta di ordinare, ma soltanto laddove può farlo! In secondo luogo, nel mondo sensibile non esiste il vuoto (58 a, cfr. 79 b-c): ossia, tutto quel che è deve essere da qualche parte (52 b). Infine, la sfera del mondo racchiude tutto ciò che è corporeo.
I quattro elementi si distribuiscono, all'interno di questa sfera, in quattro strati concentrici (33 b, 53 a, 48 a-b) tra i quali si producono degli scambi. Questi quattro strati concentrici sono coinvolti nel movimento circolare che anima l'insieme della sfera. Siccome non vi è alcun vuoto, le particelle non possono espandersi all'infinito verso l'esterno; all'interno, poi, esse possono circolare soltanto negli interstizi che traggono la loro origine dalla mancanza di omogeneità tra gli elementi e che sono di continuo colmati. Di qui una reazione a catena, che è provocata dalla "compressione implicata dal processo di rimozione" (58 b, cfr. anche 76 c e Leges, X, 849 c) e che provoca un processo (58 b) nel quale sono presenti i due tipi di movimento, sopra richiamati, che regolano ogni trasformazione di un corpo in un altro: divisione e condensazione, decomposizione e ricomposizione.
In definitiva, ci si deve rappresentare l'Universo platonico come una vasta sfera riempita da un fluido omogeneo e sprovvisto di qualsiasi caratteristica (e cioè la chṓra), la cui maggior parte è però racchiusa in involucri che delimitano la superficie esterna di ciascuno dei quattro poliedri regolari 'elementari': tetraedro, ottaedro, icosaedro, esaedro. Queste componenti elementari tendono a ripartirsi in quattro strati concentrici, tendenza contrastata dal moto di rotazione che interessa la sfera nel suo insieme. Da questo movimento risultano gli spostamenti dei poliedri regolari, ossia una modificazione della Natura per cui il fuoco diventa aria, l'aria diventa acqua e viceversa. Tale rappresentazione lascia apparire una contraddizione: nell'Universo platonico si deve tenere conto contemporaneamente del continuo, che deve caratterizzare la chṓra, e del discontinuo, ineluttabilmente instaurato dai poliedri regolari. La fisica platonica non è dunque né un atomismo come quello proposto da Leucippo e Democrito, né una fisica del continuo come quella proposta da Parmenide, Zenone di Elea e Melisso di Samo; essa è un atomismo che si sviluppa sullo sfondo di un continuo.
Pur incorrendo in tale contraddizione, si deve ammettere che ogni trasformazione di un corpo in un altro può essere spiegata in termini di interazioni e correlazioni matematiche; il mondo sensibile è infatti dominato da un'anima che presenta una struttura matematica particolarmente rigorosa, e il demiurgo ha modellato matematicamente la chṓra introducendovi i poliedri regolari. La matematica consente di applicare al mondo sensibile alcuni predicati del mondo intelligibile di cui partecipa; a ragione di ciò, il mondo sensibile si vede così rivestito di permanenza e regolarità. In ultima istanza, è la matematica che dà conto della partecipazione del mondo sensibile al mondo intelligibile. Se, infatti, il mondo sensibile è un'immagine dell'intelligibile, allora deve essere costruito matematicamente; in questa prospettiva, è la matematica che fissa i limiti della cosmologia platonica.
Scienze del vivente
L'anima, fonte di vita. Per Platone un vivente è un essere provvisto di anima, essendo quest'ultima il principio di ogni movimento spontaneo, sia fisico sia psichico. Tutte le anime, in quel che hanno di immortale, si presentano come succedanee dell'anima del mondo, la cui costituzione è descritta nel Timeo (35 a-b, v. sopra).
Gli esseri provvisti di anima sono classificati gerarchicamente. Alla sommità si situano gli dèi e i demoni; vengono poi gli esseri umani, uomini e donne, e gli animali che vivono nell'aria, sulla terra e nell'acqua; al gradino più basso si situano le piante. Così, quando si vuole parlare di 'scienza della vita', si impone una distinzione: gli esseri umani e gli animali devono essere considerati a parte, poiché si distinguono da un lato dalle piante, provviste soltanto di un'anima appetitiva, e dall'altro dagli dèi (compresi il mondo e i corpi celesti) e dai demoni, il cui corpo non è soggetto a corruzione. Tuttavia la distinzione tra essere umano e animale va colta anche in un'altra prospettiva: sia il corpo dell'uomo, sia quello della donna, nonché quello di tutti gli animali che vivono nell'aria, sulla terra e nell'acqua sono 'animati' da un'anima umana che presenta la stessa struttura di quella degli dèi e dei demoni. Di conseguenza, l'essere umano (maschio e femmina) e gli animali che vivono sulla terra, nell'aria e nell'acqua vanno considerati come esseri umani, maschi in origine, che successivamente hanno subito un processo di degenerazione in funzione di come hanno usato la ragione nella loro esistenza anteriore.
Il corpo dell'essere umano. Come tutti i viventi, l'essere umano è costituito secondo lo stesso modello dell'Universo (kósmos); possiede un'anima la cui specie razionale presenta gli stessi due cerchi che costituiscono l'anima del mondo e che si trovano soggetti alle stesse proporzioni matematiche; inoltre, il corpo umano è fabbricato a partire dai quattro elementi che costituiscono il corpo del mondo. Si può dunque dire che l'essere umano è un microcosmo (un Universo in piccolo). Due caratteristiche distinguono questo microcosmo dal mondo: contrariamente al corpo del mondo, il corpo dell'uomo è soggetto alla distruzione e la sua anima conosce una storia, che la fa passare in corpi differenti in funzione della qualità della sua contemplazione dell'intelligibile, sia quando essa è separata da un qualsiasi corpo sia quando abita un corpo (Timaeus, 90 e-92 c). In linea generale, dunque, l'essere umano può dunque essere considerato come un composto che associa provvisoriamente un'anima umana e un corpo di sesso maschile o femminile.
Due tipi fondamentali di tessuto costituiscono il corpo dell'essere umano: il midollo e la carne. Per fabbricare il midollo, il demiurgo sceglie dapprima triangoli lisci e regolari, in grado di produrre fuoco, acqua, aria e terra della forma più precisa. Questi triangoli perfetti li mescola per costituire il midollo con cui fabbrica sia il cervello sia il midollo spinale e quello osseo; il midollo è così importante perché ‒ come si vedrà ‒ ad esso si ancorano le differenti specie di anima. Il demiurgo prosegue poi il suo lavoro; dopo aver bagnato e stemperato con il midollo della terra pura, passata al setaccio, fabbrica la sostanza ossea, di cui si serve per modellare il cranio, la colonna vertebrale e tutte le altre ossa.
Utilizzando elementi composti di superfici triangolari ordinarie, il demiurgo si accinge quindi a costituire la carne con una mescolanza di acqua, fuoco e terra, cui aggiunge un lievito formato di sale e acido, anch'essi fatti di triangoli ordinari. La carne, disseccandosi, provoca l'apparizione di una pellicola: la pelle. Sul cranio, l'umidità che fuoriesce dai fori praticati nella pelle dal fuoco, e che è reimmessa sotto la pelle dall'aria, vi si radica dando origine ai peli. Da una mescolanza di osso e di carne senza lievito il demiurgo fabbrica i tendini, di cui si serve per unire le ossa tra di loro; infine, fabbrica le unghie con una mescolanza di tendini, pelle e aria.
Il corpo dell'uomo si compone dunque dei quattro elementi, che corrispondono a quattro poliedri regolari, anch'essi a loro volta costruiti a partire dalle superfici che risultano dalla disposizione di due tipi di triangoli rettangoli: isosceli e scaleni; le qualità matematiche di questi due triangoli basilari spiegano la differenza tra il midollo, ove nell'uomo si àncora l'anima, e la carne, sostanza totalmente mortale. In tale contesto, anche la biologia si ritrova matematizzata, quantunque al livello più elementare. Anche la distruzione del corpo umano mediante le malattie è descritta, al livello più fondamentale, in termini matematici: si spiega infatti con una dissociazione, o una trasmutazione, dei suoi elementi costitutivi, anch'essi passibili di associazione con i quattro elementi messi in rapporto con i quattro poliedri regolari. La morte interviene quando il midollo è gravemente danneggiato; allora, i legami che tengono l'anima unita al corpo si allentano e cedono.
Tre sistemi ‒ il sistema circolatorio, il sistema respiratorio e il sistema nutritivo ‒ spiegano il buon funzionamento del corpo umano, che può essere d'altra parte distrutto da vari tipi di malattie; tutto ciò è accuratamente descritto nel Timeo (da 77 c a 86 a). Il sistema circolatorio è descritto con il ricorso alla metafora del giardino, e la descrizione si svolge in due fasi; dapprima sono menzionate le reti di vasi (77 c-e) che trasportano il sangue in tutte le parti del corpo, poi Platone passa alla circolazione del sangue all'interno di questi vasi (77 e-78 b), che risulta dalla decomposizione degli alimenti per opera del fuoco e ha una duplice funzione, in quanto assicura la nutrizione di tutte le parti del corpo ed è il veicolo della sensazione. Il sistema respiratorio (78 a-80 d) è descritto invece a partire dalla metafora della nassa. Essa comporta due parti: una cavità centrale che si trova all'interno del tronco, fatta di fuoco, e due imbuti fatti d'aria, che passano per il naso e la bocca (78 a-d). L'intera struttura è soggetta a un movimento alternato che fa sollevare e abbassare il torace, e che continua finché dura la vita. L'aria, che è seguita dal fuoco, è di fatto soggetta a un movimento circolare; è inspirata attraverso il naso e la bocca, ed espirata attraverso il corpo in un movimento circolare che Platone assimila a varie altre specie di movimento (78 d-80 c).
La circolarità di tutti i movimenti menzionati si spiega con la volontà di dimostrarne la permanenza (v. sopra). Platone passa poi al sistema nutritivo (80 d-81 e), in cui il ruolo primario è attribuito al sangue, che risulta dalla decomposizione degli alimenti ‒ bevande e cibi solidi (80 d-e), di origine unicamente vegetale ‒ per opera del fuoco, il quale gli dà il suo colore rosso. Il fuoco, che, come si è visto, segue l'aria nel processo respiratorio, dissolve il nutrimento quando passa nello stomaco e spinge il sangue, che deriva da questa decomposizione, a introdursi nei vasi preposti a tal fine. Trasportato in ogni parte del corpo, il sangue nutre il midollo, la carne e il corpo intero (80 e-81 b). Le malattie mortali sopraggiungono quando, nutrito in modo inappropriato, il midollo ove si ancorano le differenti specie dell'anima degenera e si decompone (81 b-e).
Le malattie che distruggono il corpo umano si dividono in tre gruppi. Certe malattie sono dovute a un eccesso, a una carenza o a una cattiva distribuzione dei componenti elementari (ossia dei quattro elementi) che costituiscono il corpo umano (81 e-82 b). Altre malattie provengono da una decomposizione dei tessuti (la carne e i tendini) che, liquefacendosi, contaminano il sangue (82 b-84 d). Un terzo gruppo di malattie dipende da ciascuno degli elementi costitutivi del corpo umano (terra, acqua, aria e fuoco): si tratta delle febbri (86 a), di alcune malattie che interessano il respiro (84 d-85 a), di quelle relative al flegma (85 a-b) e alla bile (85 b-86 a).
Scienze dell'anima
Platone descrive l'anima dell'essere umano in modo molto diverso a seconda dei dialoghi. Fino alla Repubblica, essa è considerata come quel principio unico che spiega ogni movimento spontaneo, sia materiale (locomozione, ecc.), sia spirituale (conoscenza, sentimenti, ecc.); a partire dalla Repubblica, s'impone invece, con insistenza sempre maggiore, l'idea secondo la quale l'anima presenta specie che assolvono funzioni differenti; tale tema è ben chiarito nella Repubblica.
Le specie dell'anima e il loro rapporto col corpo. Le specie delle anime che muovono il corpo dei viventi ‒ quelle degli dèi, quelle dei demoni e quelle degli esseri umani (in ogni caso la specie immortale) ‒ sono fabbricate dal demiurgo a partire dalla mescolanza che è servita a costituire l'anima del mondo, anche se questa mescolanza non ha più la stessa originaria purezza (ibidem, 41 d). La specie immortale dell'anima dell'essere umano può essere perciò considerata come un succedaneo dell'anima del mondo. Vi si ritrovano pertanto i due cerchi, quello dell'Identico e quello dell'Altro, di cui consiste l'anima del mondo (43 e-44 b, cfr. 44 d) e vi si notano le stesse divisioni matematiche che obbediscono alle identiche leggi di proporzione (43 d). Proprio come l'anima del mondo, l'anima dell'essere umano assicura movimento e conoscenza e i suoi due cerchi sono mossi da un movimento rotatorio (42 c, 43 d, cfr. 44 b, d, 47 d e anche 90 d). Essa compie gli atti di conoscenza intelligibile, ed è il punto d'approdo della conoscenza sensibile (64 b); in essa poi interviene la deliberazione, che rappresenta l'aspetto pratico della conoscenza intelligibile. Questa specie dell'anima umana, fabbricata dal demiurgo stesso e non dai suoi aiutanti, è immortale (42 e, 69 c) ed è per questo divina (69 d, 45 a): è un "daímōn" (90 a).
Su questa fondamentale bipartizione tra specie mortale e specie immortale si fonda la successiva tripartizione della specie mortale. Vari passaggi nel Timeo (69 c, d, e, 70 e) ne menzionano l'esistenza, ma non sono descritte né la costituzione di questa specie, lasciata alle cure degli assistenti del demiurgo, né la sua natura. In breve, la specie mortale dell'anima umana comprende due sottospecie: una irascibile (thymós), che assicura nell'uomo le funzioni difensive, e una appetitiva (epithymía), che assicura le funzioni nutritive e riproduttive. Il termine thymós designa la specie dell'anima umana qualificata come guerriera (70 a, 90 b); d'altra parte, la specie dell'anima umana designata con il termine epithymía non può in alcun modo comprendere un discorso razionale (71 a, d), a causa della grande distanza che la separa dalla specie immortale dell'anima umana, ossia l'intelletto. È precisamente questa lontananza dall'intelletto che conduce Platone a descrivere metaforicamente la sottospecie concupiscibile dell'anima umana con i tratti di una bestia selvaggia, incatenata alla sua greppia, che grida con gran clamore (70 e).
Le diverse specie d'anima sono impiantate in parti differenti del corpo umano: la specie immortale, che corrisponde alla ragione, è situata nel cervello, mentre la specie aggressiva è situata nel midollo spinale al livello del cuore, al quale è intimamente associata, e la specie appetitiva nel midollo spinale al livello del fegato. In questa topica corporale la preminenza è attribuita al cervello sul cuore, il quale in precedenza aveva sempre mantenuto la supremazia, e l'aveva ancora in molte teorie mediche del tempo di Platone.
L'unione di anima e corpo. Se dunque l'essere umano è un composto provvisorio di anima e corpo, il problema principale è fare in modo che l'anima comandi al corpo e, quindi, che la specie immortale di questa anima resti "primitiva e ottima" (ibidem, 42 d, cfr. 71 d), che "domini in noi tutto il resto" (44 d) e assicuri l'obbedienza della specie appetitiva, con l'ausilio della specie irascibile che gioca un ruolo d'intermediazione. Al loro arrivo in un corpo, i moti della specie razionale dell'anima sono agitati in ogni direzione dal flusso delle impressioni, accresciuto dal flusso del sangue che le trasporta (77 e). La nascita e l'infanzia rappresentano dunque per l'essere umano, in queste circostanze degradato al rango di animale, momenti in cui regna il caos (43 a-44 b), poiché la specie razionale della sua anima non riesce ancora ad assicurarsi il dominio. Vi è qui una differenza essenziale tra il mondo sensibile e l'essere umano, che inizia una vita razionale dal momento in cui l'anima si unisce al corpo. Con il tempo, la situazione si stabilizza (44 b-c), e arriva a instaurarsi una provvisoria cooperazione tra l'anima e il corpo, e il luogo privilegiato di tale cooperazione è la sensazione, o percezione sensibile.
Per quanto riguarda la conoscenza le principali questioni riguardano il meccanismo della percezione sensibile e, soprattutto, quale rapporto intrattengano la percezione sensibile e la conoscenza razionale.
La percezione sensibile. La percezione sensibile presenta due facce, poiché stabilisce una relazione tra un soggetto ‒ che è un vivente dotato di corpo e anima ‒ e un oggetto situato al suo esterno. I pathḗmata (la traduzione meno inadeguata del termine resta "affezioni") non sono proprietà che risiedono in un oggetto indipendentemente dai loro effetti sul soggetto che percepisce. Non sono nemmeno, come i sensibilia nel Teeteto (153 a-157 a), qualità ‒ il bianco o il nero, per esempio ‒ esistenti soltanto in quanto percepite, e soltanto limitatamente al momento in cui lo sono. Sono invece gli effetti provocati da un oggetto situato all'esterno di un soggetto recettivo; nel Timeo (61 d-68 b) i pathḗmata sono infatti sistematicamente rapportati al corpo umano nel suo insieme, o all'una o all'altra delle sue parti. Si pone difatti una distinzione tra le sensazioni comuni, che interessano il corpo nella sua totalità, e le sensazioni particolari che interessano un organo determinato: lingua, narici, orecchie, bocca (ibidem, 65 b).
Considerata dalla parte del soggetto percipiente, la sensazione è comunicazione: ciò che è comunicato è la proprietà manifestata da un oggetto per il tramite di un movimento che trova la sua origine esteriormente. La trasmissione di tale movimento si compie in modo meccanico, da una parte all'altra, in un circuito (ibidem, 78 b-79 a, e 80 a-b), attraverso il vivente nella sua totalità, corpo e anima (77 d-e, 43 b-c). Il destinatario finale di questo processo di trasmissione è infatti la specie razionale dell'anima. Ora, la possibilità di questa trasmissione e la qualità che presenta dipendono dalla natura del recettore, e cioè, in definitiva, dall'elemento ‒ fuoco, aria, acqua o terra ‒ che predomina in tale recettore. Gli elementi infatti si distribuiscono, secondo una scala decrescente, in funzione della loro mobilità (55 e-56 a): il fuoco è l'elemento più mobile, la terra l'elemento più stabile, mentre l'aria è meno mobile del fuoco e più mobile dell'acqua. Di conseguenza, le parti del corpo costituite di terra ‒ come le unghie, i capelli, le ossa (64 b-c) ‒ e tutte quelle ricoperte di uno spesso strato di carne (75 a) trasmettono male i pathḗmata, con l'eccezione della lingua, che è un organo di sensazione specializzato (75 a 5-6). Per contro, le parti del corpo dove predomina il fuoco (come gli occhi) e dove interviene l'aria (come le orecchie) sono mirabili strumenti di trasmissione (64 c).
Come si può spiegare però che il movimento ricevuto da una parte del corpo ‒ che si tratti o no di un organo specifico: occhi, orecchie, lingua o narici ‒ sia trasmesso attraverso l'insieme del corpo verso l'anima? Al tempo di Platone non si conosce ancora il ruolo svolto dai nervi nel meccanismo della sensazione (ruolo che non sarà scoperto prima di Erofilo da Calcedone, nel III sec. a.C.), ed è pertanto il sangue che veicola nel corpo le informazioni relative alle percezioni sensibili (ibidem, 70 a-c). Il sangue è quindi un liquido rosso, proveniente, come già detto, dagli alimenti liquidi o solidi, lacerati e trasformati sotto l'effetto del fuoco (80 c-81 a), che serve innanzitutto alla nutrizione (81 a-b). L'associazione, nel caso del sangue, della funzione nutritiva da una parte e di quella della trasmissione dell'informazione sensibile dall'altra, è ben evidenziata (42 e 5-43 c 7). Il sangue presenta tre caratteristiche che spiegano perché possa essere considerato come agente di trasmissione dei pathḗmata attraverso il corpo verso l'anima; innanzi tutto, dal momento che comporta i quattro elementi, che si trovano in ogni pianta, esso è in grado di trasmettere una informazione proveniente da qualsiasi altro oggetto dell'Universo, che procede dagli stessi elementi; in secondo luogo, poiché il fuoco vi predomina, come indica il suo colore rosso, il sangue presenta una grande mobilità, caratteristica che deve possedere ogni agente destinato a trasmettere i pathḗmata ‒ conditio sine qua non della sensazione ‒; infine, il sangue circola sempre e ovunque nel corpo, di modo che è sempre e ovunque disponibile per trasmettere un'informazione, da qualsiasi parte essa provenga, attraverso il corpo fino all'anima.
Affinché si dia sensazione, il movimento provocato alla periferia del corpo dai pathḗmata deve dunque giungere all'anima, e più precisamente alla sua specie razionale. Tuttavia non è spiegato come un movimento corporeo possa trasmettere un'informazione a una realtà incorporea, qual è l'anima, e andrebbe inoltre precisato quale specie di anima sia il destinatario finale di questi movimenti in cui consistono le sensazioni. Nel Timaeus (64 b 3-6) si apprende che la trasmissione d'informazioni implicata nella sensazione deve arrivare sino al phrónimon, nel quale è difficile non riconoscere la specie razionale dell'anima.
La conoscenza razionale. La conoscenza razionale, che ha per oggetto l'intelligibile, si realizza come processo di reminiscenza: cercare di conoscere è tentare di ricordare una conoscenza già avuta in una vita anteriore, quando l'anima umana, separata da ogni corpo, contemplava l'intelligibile. Prima dell'incarnazione, infatti, l'anima ha già appreso tutto ciò di cui acquisirà nuovamente la conoscenza, nel senso stretto del termine, nel corso della sua esistenza corporea (Phaedrus, 245 d-249 d). E poiché l'anima, incarnata o no, conserva la sua identità, tale conoscenza, detenuta in modo non cosciente o latente, sembra essere la sua caratteristica essenziale. Quando poi, nel corso della sua vita incarnata, essa apprende una qualsiasi cosa, questo apprendimento consiste nella riattivazione di un apprendimento già compiuto in precedenza, e forse anche sempre già concluso.
Patologia mentale. Le cause della follia. Dopo aver descritto l'attività mentale 'normale', Platone s'interroga sui comportamenti anormali che dipendono dalla patologia mentale, dalla follia, che può essere definita come una rottura con gli usi e le abitudini consuete (ibidem, 265 a), e può essere provocata sia da una malattia umana sia da un impulso divino. Nel Fedro si evocano quattro generi di follia: la follia divinatoria che viene da Apollo, la follia iniziatica che viene da Dioniso, la follia poetica che viene dalle Muse e la follia amorosa che viene da Eros. Alla fine del Timaeus (86 b-88 b) la follia è invece considerata da un punto di vista medico, e una stessa causa (un cattivo funzionamento del corpo) è attribuita a tutti i disturbi mentali, tutti ricondotti alla stoltezza (ánoia), che presenta le due forme della follia (manía) e dell'ignoranza (amathía). Questo cattivo funzionamento del corpo può avere un'origine fisiologica o psicologica: la follia risulta da una sovrabbondanza di midollo (86 c), mentre causa dell'ignoranza, che equivale a una pigrizia della mente, sono flegmi acidi e salati (ibidem, 86 e-87 a). Inoltre, le conseguenze di questo stato del corpo possono essere aggravate da una cattiva educazione e da una riprovevole costituzione politica (87 a-b). Può succedere che l'anima diventi così potente, rispetto al corpo in cui abita, da minacciare di distruggerlo (87 e-88 a): questo accade quando si immerge con eccessivo ardore in certi studi o in certe ricerche, o quando si dedica eccessivamente all'insegnamento o alle dispute, in pubblico o in privato. Con la sua follia, l'anima può quindi suscitare nel corpo delle affezioni in grado di distruggere il suo equilibrio e di provocarne i mali.
Mantenimento e ristabilimento della salute mentale. Si pone allora il problema di sapere come assicurare il buon funzionamento del corpo e dell'anima, col fine di evitare la malattia mentale o guarirne. Il postulato che governa tutta questa sezione è il seguente: "Tutto ciò che è buono è bello e non vi è bellezza senza misura (ámetron); anche l'essere vivente, dunque, se deve esser buono, ha da esser misurato (sýmmetron)" (ibidem, 87 c). La salute risiede dunque nella proporzione, intesa come mantenimento di un rapporto (indicato dal prefisso sym-) tra le misure (métra) che indicano l'importanza relativa auspicata tra due realtà: nel vivente considerato come un tutto, si tratta di un rapporto tra anima e corpo, nell'anima si tratta invece di un rapporto tra le sue specie, e nel corpo di un rapporto tra le sue parti.
Per ritrovare la salute mentale, o per mantenerla, non v'è che un rimedio: non esercitare, o muovere, né l'anima senza il corpo né il corpo senza l'anima. Soltanto rispettando questa regola l'essere umano potrà essere "bello e insieme buono" (ibidem, 88 c), secondo l'ideale greco dell'epoca di Platone. Chi si consacra allo studio deve sviluppare il corpo praticando la ginnastica; chi si premura di modellare il corpo con la ginnastica deve peraltro dedicarsi alla musica e alla filosofia. Una stessa regola si applica contemporaneamente alle specie dell'anima e a quelle del corpo: imitare l'Universo, comprendendo e riproducendo in sé i movimenti dell'anima e del corpo del mondo. Per quanto riguarda l'anima nella sua totalità, si deve sempre attribuire la preminenza alla specie razionale (89 d-e), senza però lasciare le altre specie inattive ‒ come vuole il principio enunciato sopra, secondo il quale una specie che resti nell'inattività s'indebolisce (89 e-90 a) ‒ e sempre curando che i movimenti delle diverse specie dell'anima conservino tra loro un buon equilibrio. Per evitare che il corpo sia colpito dalle possibili affezioni degli elementi che lo compongono, nessuna sua parte deve restare a riposo; l'essere umano deve pertanto impegnarsi a trasmettere al corpo dei movimenti simili a quelli che animano la chṓra dopo che il demiurgo l'ha dotata di ordine e di misura (88 d-e). Platone enumera tali movimenti ordinandoli per importanza: (1) quello procurato dalla ginnastica, (2) quello trasmesso dalle imbarcazioni e dai veicoli che servono al trasporto, (3) quello provocato dai farmaci, e in particolare dai sistemi purgativi, di cui Platone raccomanda di non abusare (89 b-e).
Medicina
Le cure del corpo hanno l'obiettivo, almeno nel caso dei guardiani e dei filosofi, di rendere inutile la medicina (Respublica, 405 a-410 b), proprio come la cura dell'anima dovrebbe rendere inutili i tribunali. Si ritrova qui un tema sviluppato nel Gorgia (464 b-465 e), in un passo in cui Socrate spiega che vi sono due arti (téchnai) che si occupano dell'anima e due che si occupano del corpo; le prime sono relative alla politica, e sono la legislazione e l'istituzione giudiziaria ‒ l'una organizza, mentre l'altra cura ‒ mentre le due arti che si occupano del corpo sono la ginnastica, che cerca di mantenere il corpo in forma, e la medicina, che cerca di curarlo. A queste arti corrispondono quattro forme di adulazione (kolakeía): quelle relative all'anima sono la sofistica e la retorica, che corrispondono, rispettivamente, alla legislazione e al sistema giudiziario, e quelle che riguardano il corpo sono l'arte cosmetica e l'arte culinaria, che corrispondono alla ginnastica e alla medicina. Si comprende quindi come la ginnastica, che assicura la salute del corpo, abbia lo scopo di rendere inutile la medicina, proprio come la legislazione, che regola bene i rapporti tra gli uomini, ha il fine di rendere inutili i tribunali.
La ginnastica deve mirare dunque all'instaurazione e alla conservazione di un modo di vita adeguato, e ciò è ben spiegato nella lunga sezione della Repubblica dedicata all'educazione dei guardiani. L'anima, una volta formatasi con la musica, può precisare le regole che devono presiedere al buon funzionamento del corpo. Si tratta di un ribaltamento di prospettiva tipico dello stile di Platone: "Io credo che il corpo, per quanto ben formato, non sia per sua natura tale da far l'anima buona: anzi è l'anima che quando è buona dà al corpo, con la sua virtù, tutta quella perfezione di cui è capace (aretḗ)" (Respublica, 403 d). Un tale rovesciamento comporta una concezione affatto singolare della ginnastica; la maggior parte delle prescrizioni di Platone, infatti, non riguarda l'esercizio fisico ma l'alimentazione (condanna dell'ubriachezza, dieta di carni arrostite senza condimento né pasticceria; ibidem, 403 e-405 a). Un regime simile ‒ Platone lo ammette esplicitamente ‒ si allontana da quello che si impongono gli atleti, i quali passano la vita a dormire e sono soggetti a gravi e violente malattie (404 a). Ancora una volta, Platone si oppone alle pratiche in vigore ad Atene su un punto preciso e fondamentale: la ginnastica risponde a obiettivi differenti in quanto non è orientata alla competizione, ma a tutelare un buono stato di salute del cittadino e la difesa della pólis.
Critiche alla medicina. La violenta critica che Platone scaglia contro la medicina dietetica nei Libri II e III della Repubblica è molto più interessante sul piano storico che non su quello teorico; da un lato, essa contiene alcune informazioni importanti sulla medicina del IV sec., mentre dall'altro lato introduce elementi nuovi che mostrano le tensioni del pensiero platonico nell'ambito dell'etica e della politica. La diagnosi della patologia sociale che risulta da questi passi, la sua eziologia, la terapia che dovrebbe essere intrapresa sono largamente ispirate alle tesi della medicina dietetica di quel tempo. Ma allora perché questo attacco contro la medicina dietetica? Perché la patologia sociale si sviluppa contemporaneamente a questa medicina e alla proliferazione dei suoi rappresentanti. Per individualizzare la sua critica, Platone rievoca la figura di Erodico di Selimbria, che accusa di aver fatto slittare la medicina dall'efficacia terapeutica a un controllo pedante del regime di vita dei malati. Una riforma della medicina, parallela a una riforma della pólis, è indispensabile e deve rispondere a queste esigenze: circoscrivere la malattia, essere rapidamente efficace e rifiutarsi di trattare le costituzioni deficienti.
L'interesse della medicina sul piano teorico. In ogni caso, malgrado le critiche rivolte alla pratica della medicina, Platone ne riconosce l'interesse sul piano teorico, e ciò per due motivi. Nella medicina, così come in tutte le altre grandi téchnai, egli vede anzitutto un modello di sapere compiuto perché delimitato dall'obiettivo specifico del suo oggetto (la salute e la malattia del corpo), dotato di regole e di procedure razionali argomentative e perciò trasmissibili, e infine capace di provare la sua efficacia in relazione al suo campo di conoscenze e al suo ambito d'azione. Vi vede anche qualcosa di più specifico, ossia un metodo che procede per analisi e sintesi, e che può risalire dalla parte al tutto (dalla parte malata al corpo, dal corpo verso l'insieme costituito da corpo e anima). Questo particolare modo di procedere consente a Platone di munirsi del metodo per divisione (diaíresis) e riunione (synagōgḗ), che negli ultimi dialoghi assume un'importanza sempre crescente. Sotto questo profilo la medicina acquisisce una dignità epistemologica che si avvicina, pur non raggiungendola, a quella accordata alla matematica; la medicina rimane però legata a una realtà corporea e sensibile, e resta dunque lontana dall'idealità cui introduce la matematica.
D'altronde, il privilegio che Platone accorda alla medicina rispetto alle altre téchnai è confermato anche da un altro argomento, ossia che il medico esercita sul suo paziente un potere motivato non dall'interesse personale, ma da un sapere che assume la forma di una prescrizione terapeutica che fa appello alla persuasione e il cui obiettivo è la salute del paziente stesso; questo disinteresse deve costituire secondo Platone il modello del buon governo. Al filosofo-re è infatti accordato un potere destinato a curare i mali dell'anima e quelli della città, legittimato da una conoscenza del bene universale, mirante all'interesse e alla salute della città nel suo complesso, e fondato non sulla violenza e sull'ingiustizia, ma sulla persuasione.
Zoologia
Per Platone non v'è rottura radicale tra gli dèi e i demoni, tra l'uomo e gli altri viventi, e quelli che noi consideriamo 'animali' sono esseri umani reincarnati. In questa prospettiva, dall'uomo fino alla conchiglia, tutti i corpi viventi rappresentano "stati dell'anima", in quanto sono i segni della qualità di un'anima umana che s'incarna in questo o quel vivente in funzione della sua esistenza anteriore. Tutti i viventi si situano dunque lungo un continuum, dove la classificazione delle "specie" interviene tuttavia necessariamente. Alla fine del Timeo, le specie dei viventi sono messe in rapporto con i quattro elementi: gli dèi (i corpi celesti) sono associati al fuoco; gli esseri umani (tutti inizialmente generati di sesso maschile) e gli animali che camminano o si arrampicano si spostano sulla terra; gli uccelli volano nell'aria; i pesci e le bestie acquatiche vivono nell'acqua.
Per classificare le specie viventi, Platone fa uso del metodo per divisione e riunione. Nel Politico, per esempio, Platone perviene a questa conclusione, che sarà veementemente criticata da Aristotele: "Dico dunque che fin d'allora bisognava subito distinguere l'animale che ha i piedi in bipede e quadrupede, e quindi, vedendo che l'umanità partecipa della medesima classe dei volatili, nuovamente dividere la greggia bipede in bipedi implumi e in bipedi pennuti, e così, fatta questa divisione, e fin da allora chiarita l'arte di guidare gli uomini, prendere l'uomo politico e regio, e ponendolo su di essa quale auriga, affidargli le redini dello Stato quale un suo diritto, poiché è lui che possiede la scienza adatta a questo" (Politicus, 266 e-267 a). Anche se qui è applicata alla politica, questa pratica classificatoria resta legata alla zoologia; era una pratica corrente nell'Accademia e si estendeva anche al genere vegetale.
Botanica
Dopo aver fatto l'inventario delle quattro specie di viventi che popolano l'Universo, Platone evoca rapidamente, in un passo particolarmente difficile (Timaeus, 76 e-77 c), l'origine dei vegetali, che egli associa alla terza specie di anima, quella appetitiva. L'esistenza dei vegetali si ritiene giustificata dalla necessità che il corpo umano ha di ricostituirsi, al fine di permanere in vita, cibandosi di esseri dotati al pari di lui di anima, ma di un'anima assolutamente sprovvista della specie razionale: "Dopo che le parti e le membra dell'animale furono cresciute tutte insieme, siccome doveva di necessità compiere la vita nel fuoco e nell'aria, e perciò sarebbe perito disciolto e consumato da questi, gli dèi gli prepararono un soccorso. Infatti, mescolando con altre forme e sensazioni una natura affine alla natura umana, ne formarono una nuova specie di animali: e cioè gli alberi e le piante e i semi ora coltivati, che educati dall'agricoltura divennero domestici verso di noi: prima invece v'erano soltanto le specie selvatiche che sono più antiche di quelle coltivate" (ibidem, 77 a-b). La sostanza delle piante è dunque affine alla nostra (cfr. apò syngenõn, 80 e; tò syngenés, 81 a-b); esse sono composte di un corpo formato a partire dai quattro elementi e di un'anima che corrisponde alla terza specie dell'anima umana.
Un tale approccio al problema non è concepibile se non nel quadro di un incitamento alla pratica del vegetarianismo, come si constata qualche riga più in basso (ibidem, 77 c). La decomposizione delle piante all'interno del corpo umano permette la costituzione del sangue, che nutre tutti gli altri tessuti; le piante permettono così al corpo umano, che, a differenza del corpo del mondo, può essere distrutto da aggressioni esterne (quelle del fuoco e dell'aria), di ricostituirsi senza cibarsi di animali, fatto importante nel quadro di una dottrina della metemsomatosi (o reincarnazione) ove gli animali possono essere considerati come degli uomini.
Le scienze della Terra e del suo popolamento
A queste scienze della Natura, si devono aggiungere quelle che si possono chiamare 'scienze della Terra', come la geologia, e 'scienze sociali': storia, sociologia e scienze politiche. In Platone si trova infatti un certo numero di informazioni sulla struttura della Terra, in superficie e in profondità, e sul suo popolamento.
Nel mito che Socrate narra poco prima della morte (esposto nelle ultime pagine del Fedone) è proposta, nel quadro di un racconto escatologico, una rappresentazione della Terra, alla superficie e in profondità. Socrate comincia (Phaedo, 108 e-111 c) ricordando qualche dato cosmologico: la Terra, che è sferica, si trova al centro dell'Universo, dove rimane immobile. La parte abitata dagli esseri umani non è la totalità della Terra che, essendo un corpo molto grande, comprende tre regioni: quella dove dimorano gli esseri umani, un'altra al di sopra e una terza al di sotto. Per un osservatore situato sopra di essa, la vera Terra presenterebbe l'aspetto di un pallone, ove i colori sono molto più puri e brillanti, le stagioni temperate, la vita vegetale e animale più ricca. Gli esseri umani che la abitano sono esenti da malattie e vivono più a lungo; i loro sensi e la loro intelligenza sono più acuti; essi hanno relazioni dirette con gli dèi, che convivono e parlano con loro, rivelando l'avvenire. Per gli esseri umani che vi soggiornano, esistono tre possibili habitat: o all'interno del continente, o sulle rive di questo, bagnato dall'aria come fosse un mare, oppure su isole più lontane dal continente e completamente circondate d'aria (le Isole dei Beati, o Isole Fortunate).
Questa parte superiore della Terra presenta una forma sferica ed è disseminata di un gran numero di depressioni, nelle quali si depositano acqua e aria. Nel fondo di una di queste depressioni si trova il mare attorno al quale abitano gli esseri umani. Poiché in queste depressioni l'aria è mescolata al vapore acqueo, i colori sono poco brillanti e, in confronto a quel che esiste sulla parte alta della Terra, sia la vita vegetale sia quella animale e umana sono segnate dall'imperfezione; spesso malati, gli uomini hanno intelligenza e sensi meno acuti (ibidem, 110 b-111 c). Oltre alle depressioni della Terra di mezzo, dove abitano gli esseri umani, vi sono altre depressioni dell'interno della Terra, che costituiscono degli abissi le cui aperture sono più o meno larghe rispetto alle depressioni conosciute dagli esseri umani e che le prolungano in maggiore o minore profondità. Queste depressioni comunicano tra loro tramite orifizi di diversa larghezza e vie di transito, il che implica l'esistenza di laghi e fiumi anche all'interno della Terra (ibidem, 111 c-113 c). Da dove provengono i flutti che alimentano questi fiumi e come si spiega la corrente che li anima? Si tratta dell'oscillazione di un'enorme onda. In una faglia centrale, il Tartaro, che attraversa l'interno della Terra da parte a parte, l'acqua sale e scende senza posa, con un movimento che può essere paragonato a quello dell'aria nella respirazione. È dal Tartaro che provengono i quattro grandi fiumi sotterranei ‒ Oceano, Acheronte, Piriflegetonte e Cocito ‒ ed è lì che infine si gettano (v. tab. 6).
Storia. Presentandosi come riformatore politico, Platone deve prestare attenzione alle società che l'hanno preceduto, e a quella in cui vive, allo scopo di proporre un modello alternativo accettabile. I suoi rapporti con la storia sono particolarmente ambigui, e proprio a causa dei due presupposti che fondano la sua metafisica: quello dell'esistenza delle Idee che rappresentano la vera realtà, di cui le cose sensibili non sono altro che immagini, e quello dell'esistenza dell'anima, in cui consiste la vera identità dell'essere umano e che può reincarnarsi in più corpi umani, o anche animali, differenti. Se il mondo delle cose sensibili è soltanto un mondo di immagini, perché descrivere le peripezie di entità di inferiore consistenza ontologica? La storia è più simile a una tragedia o a una commedia. Inoltre, il destino degli uomini si gioca soltanto parzialmente nel corso della loro esistenza terrena, che è determinata, in ultima analisi, dalla qualità della contemplazione che la loro anima ‒ incarnata o anche separata (e cioè, fuori della storia) ‒ ha precedentemente avuto delle Forme.
Ciò non toglie che in un certo numero di dialoghi ‒ tra cui il Menesseno, il Timeo e il Crizia, e il Libro III delle Leggi ‒ Platone mostri un reale e profondo interesse per la storia: quella della Grecia, certamente, ma anche quella degli altri popoli. Il ricorso agli storici, e soprattutto a Erodoto e Tucidide, è molto più importante di quanto non si sia finora supposto e ciò che Platone prende in prestito da questi storici non riguarda soltanto i testi, ma anche il metodo; un metodo che implica una rigorosa e critica raccolta delle informazioni e severe procedure di verifica. Platone, tuttavia, non pratica la storia in sé stessa, poiché considera che le vere cause degli avvenimenti riferiti da uno storico restino inaccessibili. La spiegazione ultima del successo o del fallimento delle póleis e dei popoli dipende dall'esame della presenza o assenza di virtù, ovvero di un elemento divino in tali póleis o popoli. Anche se il progetto generale del filosofo non è propriamente storico, esso comunque testimonia un grande interesse per la storia, considerata come una ricerca rigorosa avente per oggetto il passato.
Scienze sociali e politiche. Nella Repubblica (in dieci libri) e nelle Leggi (in dodici libri) Platone descrive il modello della società che vorrebbe vedere realizzata. Parecchie sue osservazioni rispondono alla descrizione della società del suo tempo, altre rimandano a un progetto da realizzarsi; la ricchezza dei dettagli, ove la matematica svolge un ruolo considerevole, e la coerenza della presentazione dimostrano fino a che punto Platone prendesse sul serio questi accenni.
Questo atteggiamento è evidente soprattutto per quanto riguarda la critica della tradizione, vale a dire del mito, dove Platone si rivela osservatore perspicace prima di mostrarsi critico impietoso (unico aspetto di solito considerato come tipicamente platonico); la stessa ambivalenza si estende anche ai costumi e alle leggi. Nel Libro VII della Repubblica e nelle Leggi Platone compila un interessante inventario delle differenti costituzioni e delle loro trasformazioni. La completezza di questo inventario e la sottigliezza descrittiva hanno aperto la strada a una riflessione sull'organizzazione politica delle società, che, dopo Platone, prosegue in un contesto certamente differente, ma sempre con lo stesso spirito di coerenza e di rigore.
L'eredità platonica e l'Accademia
Lo studio dell'antica Accademia si scontra con due difficoltà considerevoli; in primo luogo, non ci restano che frammenti di opere che dovettero essere numerose e consistenti; inoltre, la nostra fonte più importante per la conoscenza del pensiero dei membri dell'antica Accademia rimane Aristotele, ma Aristotele ‒ lo si è detto ‒ non è obiettivo. Stando a certe testimonianze, l'Accademia sarebbe stata fondata da Platone nel 387, al ritorno dal suo primo viaggio nell'Italia meridionale, dove aveva incontrato alcuni pitagorici, tra cui Archita di Taranto, e in Sicilia, dove si era recato alla corte di Dionisio I il Vecchio, tiranno di Siracusa, facendo la conoscenza di Dione. L'incontro di Platone con i pitagorici, soprattutto con Archita di Taranto (Lettere, VII), sembra sia stato particolarmente decisivo per quanto concerne la priorità poi accordata alla matematica, ma nessuna indiscutibile testimonianza storica permette di dire di più con sicurezza. Platone stabilì la sua Scuola, a sue spese, in un terreno coltivato ad alberi e irrigato da sorgenti, il parco consacrato all'eroe Academo, in mezzo al quale si levava un ginnasio, sulla strada di Eleusi, nei pressi del fiume Cefiso, non lontano da Colono; lo scopo ‒ secondo il programma esposto nei Libri VI e VII della Repubblica ‒ era di dare una formazione filosofica a giovani che, per lo più, miravano a giocare un ruolo attivo nella politica, come era normale all'epoca; l'Accademia conobbe rapidamente un grande successo ed entrò ben presto in conflitto con la scuola di Isocrate, dove s'insegnava soprattutto la retorica.
Alla morte di Platone, nel 348/347, suo nipote Speusippo, designato da Platone stesso, subentrò come scolarca, capo dell'Accademia; dopo la morte di Speusippo, sembra che s'instaurasse un vero meccanismo elettorale. I primi scolarchi che succedettero a Speusippo furono Senocrate, Polemone, che ebbe come discepolo Crantore, e infine Cratete di Atene. Non si conosce l'organizzazione dell'insegnamento nell'Accademia; sembra tuttavia che Platone avesse riunito attorno a sé amici e soci, incaricati di discipline speciali, fra i quali i più noti furono Aristotele, Speusippo, Senocrate, Filippo di Opunte, Ermodoro di Siracusa, Eraclide Pontico, Eudosso di Cnido, Estiea di Perinto e Teeteto.
Le opere di Aristotele illustrano l'orientamento enciclopedico delle ricerche condotte nell'ambito dell'Accademia; i due immediati successori di Platone alla guida della Scuola scrissero poi alcune opere che proponevano classificazioni di cui non è ben noto il contenuto. Eudosso, celebre per i suoi lavori sulle proporzioni (Libro V degli Elementi di Euclide) e sull'astronomia, sarebbe anche autore di un Periplo della Terra. Le indagini di Filippo di Opunte vertevano sui fenomeni celesti (astronomia, misurazione del tempo, ecc.) e sui segni che permettevano di osservare e d'interpretare questi fenomeni (ottica, matematica, ecc.); Eraclide Pontico s'interessò a tutto quello che riguardava le matematiche e la fisica, ed Ermodoro di Siracusa alla storia di queste discipline. Si deve includere in questo primo gruppo anche un certo numero di matematici e di astronomi, come Menecmo, che per primo si sarebbe interessato alle sezioni coniche, suo fratello Dinostrato, Anfinomo, Aminta, Ateneo, Ermotimo, Callippo, che nell'astronomia raffinò il sistema delle sfere, e Theudios di Magnesia, che avrebbe scritto degli Elementi alla maniera di Euclide. Altri personaggi menzionati nelle Lettere attribuite a Platone, tra cui Eufreo di Oreo (V), Erasto e Corisco (VI), dovettero altresì frequentare l'Accademia.
Vi erano discussioni tra accademici di diverso orientamento. Secondo la testimonianza di Proclo (In primum Euclidis elementorum librum commentarii, 77, 7-17 e 78, 8-20), Speusippo e Menecmo avrebbero discusso sulla questione se le proposizioni derivanti dai principî si chiamassero tutte 'teoremi', come avrebbe voluto Speusippo, 'problemi', come sosteneva Menecmo, oppure se si dividessero in teoremi e problemi. In fin dei conti, l'Accademia sembra essere stata sin dall'inizio un luogo di discussione tra ricercatori, piuttosto che un'istituzione volta alla trasmissione autoritaria di un corpo di dottrine riservate. Ciò va ricordato e sottolineato; né Aristotele né alcuno dei successori di Platone a capo dell'Accademia mantennero nella sua ortodossia il nocciolo del pensiero del fondatore, e cioè la dottrina delle forme intelligibili, le Idee. D'altronde, se si considerano i rapporti intrattenuti da Platone e Speusippo con Dione ‒ che dopo essere divenuto discepolo di Platone e avere anche frequentato l'Accademia, ritornò in Sicilia per impadronirsi del potere ‒ nell'Accademia l'azione politica sembra aver occupato un posto importante, insieme all'elaborazione delle teorie astronomiche e allo sviluppo della geometria.
Tutto induce a credere, inoltre, che sul modello del metodo geometrico nell'ambito dell'Accademia fu intrapresa la ricerca di principî sempre più elevati; questa ricerca ‒ di cui il Filebo potrebbe aver conservato traccia ‒ sembra sia stata la base di quel sistema di principî da alcuni qualificato "dottrine non scritte" e che essi attribuiscono a Platone stesso. Coloro che si oppongono a una simile interpretazione sostengono che queste dottrine non danno l'immagine del vero Platone, ma quella del Platone che fu oggetto di discussioni all'interno dell'Accademia; di qui il loro interesse su un piano strettamente storico. In ogni caso, con il passare degli anni le considerazioni di ordine metafisico ed epistemologico sembrano aver sovrastato e poi eclissato le ricerche di ordine matematico e scientifico.
Dopo la morte del fondatore, l'Accademia restò fedele ai suoi orientamenti e s'impegnò fondamentalmente a sistematizzare, diffondere e difendere il pensiero del Maestro nei confronti di altre scuole che proponevano un pensiero diverso: il Liceo (aristotelismo), il Portico (stoicismo) e il Giardino (epicureismo). Questa attività d'insegnamento s'inseriva nel quadro di un'istituzione che non aveva un vero statuto associativo, in quanto tale statuto non esisteva nel diritto ateniese; sembra infatti che l'Accademia ‒ giuridicamente non definita nemmeno dal possesso della proprietà acquistata da Platone ‒ istituzionalmente non esistesse se non al momento delle elezioni, che facevano di un accademico scelto dai suoi pari il successore di Platone, ossia uno "scolarca".
Bibliografia
Brisson 1974: Brisson, Luc, Le même et l’autre dans la structure ontologique du Timée de Platon. Un commentaire systematique du Timée de Platon, Paris, Klincksieck, 1974 (2. éd. revue et augmentée, Sankt Augustin, Academia Verlag, 1994).
– 1997: Brisson, Luc, Perception sensible et raison dans le Timée, in: Interpreting the Timaeus-Critias, edited by Tomás Calvo and Luc Brisson, Sankt Augustin, Academia Verlag, 1997, pp. 307-316.
Bruins 1951: Bruins, Evert M., La chimie du Timée, “Revue de métaphysique et de morale”, 56, 1951, pp. 269-282.
Cambiano 1971: Cambiano, Giuseppe, Platone e le tecniche, Torino, Einaudi, 1971 (nuova ed. riv. e aggiornata: Roma-Bari, Laterza, 1991).
Caveing 1982: Caveing, Maurice, La constitution du type mathématique de l’idéalité dans la pensée grecque, Lille, Université de Lille III, Atelier national de reproduction des thèses, 1982, 3 v.
Cherniss 1944: Cherniss, Harold Fredrik, Aristotle’s criticism of Plato and the Academy, Baltimore (Md.), The Johns Hopkins University Press, 1944.
Cornford 1937: Plato’s cosmology. The Timaeus of Plato, translated with a running commentary by Francis Macdonald Cornford, London, K. Paul, Trench, Trubner & Co.; New York, Harcourt, Brace, 1937.
Dicks 1970: Dicks, D.R., Early Greek astronomy to Aristotle, London, Thames & Hudson, 1970.
Dombrowski 1981: Dombrowski, Daniel Anthony, Plato’s philosophy of history, Washington (D.C.), University Press of America, 1981.
Fowler 1987: Fowler, David H., The mathematics of Plato’s Academy. A new reconstruction, Oxford, Clarendon Press; New York, Oxford University Press, 1987 (2 ed.: 1989).
Hirsch 1997: Hirsch, Ulrike, Sinnesqualitäten und ihre Namen (zu Tim. 61-69), in: Interpreting the Timaeus-Critias, edited by Tomás Calvo and Luc Brisson, Sankt Augustin, Academia Verlag, 1997, pp. 317-324.
Knorr 1990: Knorr, Wilbur R., Plato and Eudoxus on the planetary motions, “Journal for the history of astronomy”, 21, 1990, pp. 313-329.
Krämer 1994: Krämer, Hans Joachim, Die Philosophie der Antike, in: Grundriss der Geschichte der Philosophie, Basel, Schwabe, 1983-; v. I.4: Die hellenistische Philosophie, 1994, pp. 1-174.
Lloyd 1991: Lloyd, Geoffrey Ernest Richard, Plato on mathematics and nature, myth and science, in: Methods and problems in Greek science, Cambridge-New York, Cambridge University Press, 1991, pp. 335- 351.
Miller 1962: Miller, H.W., The aetiology of disease in Plato’s Timaeus, “Transactions and proceedings of the American philological association”, 93, 1962, pp. 175-187.
Müller 1975: Müller, Carl Werner, Die Kurzdialoge der Appendix Platonica. Philologische Beiträge zur nachplatonischen Sokratik, München, W. Fink, 1975.
O’Brien 1984: O’Brien, Denis, Theories of weight in the ancient world. Four essays on Democritus, Plato, and Aristotle. A study in the development of ideas, Paris, Les Belles Lettres; Leiden, E.J. Brill, 1981-1984, 2 v.; v. II: Plato, weight and sensation.
– 1997: O’Brien, Denis, Perception et intelligence dans le Timée de Platon, in: Interpreting the Timaeus-Critias, edited by T. Calvo and L. Brisson, Sankt Augustin, Academia Verlag, 1997, pp. 291-305.
Pohle 1971: Pohle, W.B., The mathematical foundation of Plato’s atomic physics, “Isis”, 62, 1971, pp. 36-46.
Pradeau 1997: Pradeau, Jean-François, Le monde de la politique. Sur le récit Atlante de Platon, Timée (17-27) et Critias, Sankt Augustin, Academia Verlag, 1997.
Skemp 1947: Skemp, Joseph B., Plants in Plato’s Timaeus, “Classical quarterly”, 41, 1947, pp. 53-60.
Solmsen 1968a: Solmsen, Friedrich, Die Entstehung der Wissenschaften, in: Solmsen, Friedrich, Kleine Schriften, Hildesheim, G. Olms, 1968, 3 v.; v. I, pp. 316-325.
– 1968b: Solmsen, Friedrich, Greek philosophy and the discovery of the nerves, “Museum Helveticum”, 18, 1961, pp. 150-197; ora in: Solmsen, Friedrich, Kleine Schriften, Hildesheim, G. Olms, 1968, 3 v.; v. I, pp. 536-582.
– 1968c: Solmsen, Friedrich, Plato and the unity of science, in: Solmsen, Friedrich, Kleine Schriften, Hildesheim, G. Olms, 1968, 3 v.; v. I, pp. 326-331.
Vegetti 1973: Vegetti, Mario, Nascita dello scienziato, “Belfagor”, 28, 1973, pp. 641-663.
– 1995: Vegetti, Mario, La medicina in Platone, Venezia, Il Cardo, 1995.
Vlastos 1975: Vlastos, Gregory, Plato’s universe, Seattle (Wash.), University of Washington Press; Oxford, Clarendon Press, 1975.