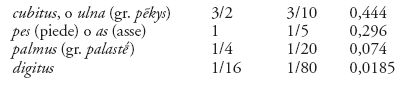Scienza greco-romana. Ingegneria
Scienza greco-romana. Ingegneria
Ingegneria
A rigore, un'ingegneria greco-romana antica non esiste. Esistevano ed erano oggetto di definizione e di trattazione specifica la meccanica (v. cap. XXVIII), l'architettura (v. oltre, parr. 1 e 2) e le discipline che insegnavano a costruire macchine da guerra (belopoietica), porti (limenopoietica), planetari (sferopoietica) e così via. Sia queste ultime discipline sia l'architettura erano spesso considerate branche della meccanica, anche se non manca tra gli antichi chi vedeva lo studio delle macchine piuttosto come parte dell'architettura o dell'arte del misurare; a proposito di questa ultima arte, nel successivo par. 3 si riportano le notizie principali sulla metrologia greco-romana e sull'aritmetica sia greca sia romana, qui vista specialmente, anche se non esclusivamente, come disciplina per fare conti con i numeri (misure) ottenuti dalle operazioni di misurazione.
Il termine moderno 'ingegnere' non ha un diretto equivalente nella cultura antica e non traduce in modo soddisfacente nessuno dei vocaboli che troviamo nelle fonti antiche: da mechanicus a technítēs (artefice), allo stesso architectus e dēmiourgós (artigiano, mastro). Da un lato, i responsabili della costruzione di navi o di macchine da guerra erano spesso chiamati 'architetti'; dall'altro lato, gli 'architetti' della cattedrale di Santa Sofia a Costantinopoli sono definiti da Procopio di Cesarea (500 ca.-560 ca.) mēchanikoí o mēchanopoioí (Aedificia I, 1, 24, 71, 76; II, 3, 11). Vi è un'intera gamma di espressioni (architéktōn, oikodómos, tektonikós) che denotano tutte la funzione di costruttore/architetto, e lo stesso si verifica per i costruttori e gli addetti dei dispositivi di irrigazione: téktones orgánōn (costruttori di strumenti), epistámenoi organízein (esperti di strumenti), mēchanárioi, mēchanoúrgoi (meccanici). L'ingegnere antico sarebbe quindi una figura al crocevia tra tutti questi campi (per i quali esisteva una notevole tradizione scritta) e altre forme di conoscenza, presenti soprattutto nella cultura orale e identificabili come téchnai o artes: pittura, falegnameria, lavorazione dei metalli, ecc.
Pur tenendo presente che gli architetti, con molta probabilità, erano impiegati anche come 'ingegneri' e viceversa, rimane poco chiaro quali esattamente fossero le distinzioni tra un ruolo e l'altro. Spesso queste distinzioni sembrano indicare differenze di prestigio e status e connotare, per esempio, la collocazione di un certo individuo nella gerarchia decisionale e amministrativa relativa alla costruzione di un'opera pubblica. Fino a qual punto però queste diversità erano anche di ordine epistemico? In quale modo cioè la conoscenza di un oikodómos differiva da quella di un architéktōn? Se, generalizzando, possiamo dire che maggiori conoscenze si traducevano in una superiorità di status, non è tuttavia possibile caratterizzare in modo univoco né i meccanismi attraverso i quali queste conoscenze erano riconosciute e valutate, né di quali conoscenze esattamente si trattava.
Lo status sociale dei rappresentanti del sapere tecnico è stato ed è tuttora argomento molto dibattuto. I meccanismi di promozione sociale e di riconoscimento, infatti, variavano notevolmente; si andava da forme di patrocinio personale simili a quelle di cui godevano poeti o filosofi a casi in cui il successo professionale era dovuto soprattutto alle competenze tecniche, magari dimostratesi particolarmente utili in situazioni di emergenza. Secondo le testimonianze pervenuteci, spesso epigrafiche, molti architetti e ingegneri erano membri dell'esercito o, specialmente nei primi due secoli dell'Impero, liberti. Ci sono, tuttavia, chiare indicazioni del fatto che, almeno nella Tarda Antichità, lo stato sociale degli architetti, per esempio, poteva essere molto alto; Simmaco menziona infatti due architetti, responsabili di lavori pubblici, che avevano rango senatoriale (Relationes, XXV). In ogni caso, architetti e ingegneri non costituirono mai un gruppo omogeneo, né dal punto di vista della composizione sociale, né da quello dell'educazione ricevuta; alcuni erano di formazione più o meno esclusivamente artigianale, altri erano non soltanto perfettamente in grado di leggere e scrivere, ma anche interessati ad accrescere quanto più possibile il proprio prestigio intellettuale e quello della propria disciplina.
Il sapere tecnico degli ingegneri greco-romani, abbracciando un'ampia gamma di discipline, pratiche e teoriche, proprie di un sapere eclettico, rispecchia in un certo modo la molteplicità della loro composizione sociale, il loro situarsi al crocevia di culture 'alte' e 'basse'. Una caratteristica comune a molti trattati tecnici è, infatti, il desiderio dell'autore di presentare la propria disciplina sia come una forma di sapere affine, o non estraneo, ad altri saperi quali la matematica, la filosofia o il diritto, sia come una conoscenza capace di produrre risultati concreti, spesso a livello 'pubblico': un sapere quindi dotato di notevoli valenze sociali e politiche.
In quale misura i testi di ingegneria erano però effettivamente utilizzati nella pratica? Sono stati avanzati molti dubbi sul fatto che gli ingegneri, coloro cioè che nell'Antichità costruivano effettivamente gli edifici e le macchine, ricevessero un'educazione di tipo liberale e fossero quindi in grado di leggere. Una posizione di questo tipo presuppone che la loro formazione si basasse su un semplice apprendistato realizzato presso botteghe artigiane o in famiglia e non comprendesse l'alfabetizzazione.
Effettivamente, in un buon numero di casi i testi tecnici hanno chiari riscontri archeologici. Per esempio, l'esistenza di alcuni edifici descritti da Vitruvio è stata confermata da frammenti di una pianta marmorea dell'Urbe e le macchine belliche rappresentate nei bassorilievi della colonna traiana sono molto simili a quelle che Erone descrive in un trattato sulla cosiddetta 'cheiroballístra' (o chirobalista, balestra portatile detta anche 'falarica'), di cui è sopravvissuto soltanto un ampio frammento. O ancora, nell'ambito delle ricerche sugli agrimensori romani, la cui preparazione matematica includeva lo studio di Euclide e di Erone, estensive ricognizioni sul territorio hanno rivelato l'esistenza di centuriazioni (particolari divisioni territoriali) corrispondenti a schemi e relazioni aritmetiche rintracciabili in alcuni dei testi di agrimensura a noi pervenuti. Nei trattati di meccanica o, in generale, di matematica troviamo spesso anche problemi matematici specificamente legati a situazioni pratiche, tipo quello della duplicazione del cubo o quello, secondo Pappo di Alessandria molto comune in architettura, di trovare la larghezza di un cilindro in cui entrambe le basi siano state troncate lungo una linea irregolare (Collectio mathematica, VIII, 1072, 30-1076, 11). Non soltanto, dunque, il valore dell'esperienza diretta non è mai negato in questi testi; molti autori tengono a precisare che sono 'ingegneri' praticanti, affermazione che pare accertata, con modalità e livelli di competenza diversi, per Filone, Vitruvio, Erone, Frontino.
Peraltro anche in quei testi che si presentano più esplicitamente come manuali tecnici e come guide per attività concrete, sono spesso contenuti sia segmenti di matematica 'teorica' sia aneddoti storici o moralistici sia asserzioni della necessità che il 'tecnico' abbia una formazione culturale che includa giurisprudenza (indispensabile nei casi, numerosissimi, in cui la tecnica aveva ripercussioni sociali forti, per il che basta pensare a opere pubbliche come gli acquedotti), ma anche filosofia e storia naturale. Talvolta quest'elenco comprende un'intera gamma di discipline 'scientifiche', quali ottica, acustica, musica, prospettiva o scenografia; in alcuni casi l'architettura o la meccanica sono definite senza mezzi termini 'filosofia' e incluse tra le arti liberali. Anche la legislazione relativa ad architetti e ingegneri specifica che i giovani da avviare a tali professioni 'tecniche' debbano essere non digiuni di studi liberali (liberales litteras). Nella Collezione di Pappo, la meccanica comprende, accanto a una parte teorica includente geometria e aritmetica, anche una parte manuale, nella quale rientrano, tra l'altro, la pittura, la falegnameria e l'architettura. Pappo specifica che, data la grande quantità di conoscenze che afferiscono alla meccanica, sarebbe un segno di particolare merito intellettuale padroneggiare sia la parte teorica sia quella manuale, ma questo non è alla portata di tutti, così che alcune persone eccelleranno nella prima, altre nella seconda.
Al di là del ruolo che questi manuali ebbero effettivamente nella formazione degli ingegneri e nella pratica - questione questa di non facile soluzione -, i destinatari di tali testi erano probabilmente molteplici, non soltanto e non necessariamente colleghi dell'autore, ma anche un pubblico genericamente 'colto', quando non addirittura un patrono, potenziale o reale che fosse. Nel complesso, dunque, è possibile identificare un tratto comune alle nostre fonti, non un consenso sui contenuti specifici della conoscenza tecnica, quanto il fatto che essa ha sempre una forte valenza 'pubblica'.
Vitruvio
di Serafina Cuomo
Dopo una lunga discussione su architettura, astronomia e idromanzia, il Libro X e conclusivo del De architectura è dedicato interamente alle macchine. Vitruvio sembra essere a conoscenza di molti degli sviluppi tecnologici di epoche precedenti; menziona di frequente Archimede e Ctesibio, ma anche molti altri autori, da Varrone a Democrito, da Archita di Taranto a Platone a Pitagora. Inoltre, in più di un'occasione si rifà alla propria esperienza diretta oppure a ciò che gli è stato insegnato. Le fonti di autorità sono dunque molteplici e Vitruvio le elenca nel resoconto che dà dell'astronomia (IX, 1, 14), adducendo le ragioni per cui una sua affermazione è degna di fede: innanzitutto, res, che va intesa come l'esperienza diretta, poi ratio, termine usato in genere nel De architectura per indicare tutto ciò che ha come base l'intelletto e il ragionamento (quindi anche il calcolo numerico) e, infine, la testimonianza degli antichi.
Il Libro X descrive sia macchine usate in tempo di pace sia macchine belliche. Le prime sono soprattutto attrezzi per sollevare, spostare o misurare pesi, per esempio vari tipi di carrucole multiple, di uso comune in edilizia, oppure pompe per sollevare l'acqua (il tympanum, a forma di ruota, la vite senza fine e una pompa pneumatica attribuita a Ctesibio) e, infine, un organo idraulico, anch'esso attribuito a Ctesibio, e un odometro, cioè uno strumento che applicato alle ruote di un carro avrebbe permesso di calcolare la distanza percorsa. In linea con la tradizione greca, Vitruvio definisce machina un insieme concreto (e materia coniunctio) la cui funzione precipua è quella di sollevare pesi, e ne distingue tre tipi: macchine 'acrobatiche', che permettono di scalare muri; 'pneumatiche', cioè azionate da movimenti d'aria; infine, macchine da trazione. Quest'ultimo tipo si divide a sua volta in macchine azionate meccanicamente, cioè da più di una persona, e macchine azionate in modo strumentale (organicos, scrive Vitruvio traslitterando il termine greco), da una sola persona. Le macchine descritte sono per lo più presentate come già esistenti, sebbene non necessariamente di uso comune e la trattazione è più una descrizione di uno stato di fatto che una proposta di innovazioni. Lo stesso si verifica per le macchine da guerra; oltre ad analizzare alcuni dispositivi da assedio già noti, come l'ariete e la testuggine, Vitruvio fornisce una serie di tavole standardizzate, contenenti tutte le misure per realizzare catapulte di una determinata grandezza.
La tecnologia militare è un caso a parte nella storia dell'ingegneria antica. Innanzitutto, essa ebbe sempre un rapporto privilegiato con il potere politico; il trattato di Vitruvio è infatti dedicato a Ottaviano Augusto, e l'autore dichiara di avere lavorato come ingegnere bellico; secoli più tardi, l'anonimo autore del cosiddetto De rebus bellicis (337-378 d.C.) non soltanto dedicherà la propria opera, scritta sotto forma di lettera, a due imperatori (non meglio identificati), ma includerà anche nella sua trattazione, oltre a proposte di riforma numismatica e amministrativa, la descrizione di alcune macchine da guerra, presentate come funzionali alla riforma dello Stato e quindi capaci di assolvere una funzione non soltanto militare ma, in senso non troppo lato, politica. È importante poi ricordare la ricchezza delle testimonianze, letterarie e archeologiche, relative alla tecnologia militare di cui disponiamo (tanto da permettere in alcuni casi di ricostruire catapulte perfettamente funzionanti), come anche la presenza di una nozione di 'progresso' che l'Antichità elaborò in rapporto a tale tecnologia. Scrittori come Filone di Bisanzio (III sec. a.C.) ed Erone furono in grado di ricostruire lo sviluppo della propria disciplina, indicandone i miglioramenti verificatisi nel corso del tempo e strutturando tale percorso in termini anche epistemologici e di elaborazione di nuovi metodi conoscitivi. La scoperta di un rapporto matematico tra le dimensioni complessive di una catapulta e il diametro del foro che contiene la molla di torsione, avvenuta, si pensa, intorno alla prima metà del III sec. a.C., fu spiegata, per esempio, come risultato dell'accumulazione di esperienze precedenti, stimolate dall'impulso alla ricerca bellica dato dai monarchi alessandrini. La scoperta di tale rapporto matematico permette di formulare il problema della costruzione di una catapulta di determinate dimensioni nei termini di un problema geometrico, e precisamente quello della duplicazione del cubo, equivalente a trovare due medie proporzionali a due segmenti dati (v. cap. XVII, Tav. I). Il testo di Filone contiene, infatti, una soluzione a tale problema, che tra l'altro è la più antica pervenutaci direttamente.
Tutto ciò è, in un certo senso, tesaurizzato da Vitruvio, che sintetizza nella sua opera circa due secoli di ricerche e può così fornire a un potenziale ingegnere un sommario di tutte le proporzioni necessarie a costruire una macchina in grado di scagliare un proiettile di un dato peso oppure una freccia di una data lunghezza. Vitruvio omette la descrizione di alcune macchine da guerra, a suo giudizio talmente semplici che tutti sono in grado di costruirle: scale, gru e così via. In altri casi dubita che un lettore non esperto di matematica possa comprendere quanto egli dice; per esempio, nella descrizione di uno dei dispositivi di irrigazione, la coclea o vite di Archimede della fig. 3 (ma nel De architectura non vi è menzione della storia che attribuisce al siracusano questa invenzione), Vitruvio specifica che la vite deve essere inclinata secondo il metodo con cui è descritto il triangolo rettangolo pitagorico, con una particolare proporzione tra i lati (X, 6, 4). Il richiamo è al capitolo IX del De architectura, dove è specificato che la ratio in questione è utile per molte cose, soprattutto misurazioni, ed "expedita" (adatta) nelle costruzioni di edifici o, come si vede in seguito, di alcune macchine (IX, praef., 6-8). Altri riferimenti all'importanza della matematica ricorrono nella sezione dedicata alle macchine belliche, dove l'obiettivo è più specificamente l'accuratezza nel cogliere il bersaglio e la rapidità nel costruire catapulte ben proporzionate, il che richiede una forma di conoscenza il più affidabile possibile. Poiché le macchine lancia-proiettili sono costruite in proporzione al proiettile da scagliare, il loro funzionamento, dice l'autore, non è expeditum per tutti, ma solamente per coloro che hanno familiarità con numeri e moltiplicazioni (X, 11, 1).
Vitruvio non soltanto descrive dettagliatamente diverse macchine, ma esprime con chiarezza il valore di tali invenzioni. Una delle parole che ricorrono più spesso è probabilmente utilitas, ma va detto che la gamma semantica di questo termine non coincide necessariamente con quello della nostra 'utilità'. In ogni caso, non vi è dubbio che le macchine o gli edifici dell'Antichità assolvessero a una qualche funzione e in questo senso fossero 'utili'; per esempio, un acquedotto doveva condurre l'acqua, un ponte permettere i trasporti e non crollare quando un pesante carro vi passava sopra, una catapulta scagliare proiettili. A tale riguardo, miglioramenti erano sempre possibili; per esempio, alcune catapulte avevano maggiore gittata di altre, e si era a conoscenza della maggiore o minore resistenza o elasticità di alcuni materiali. Un'ulteriore sfumatura è data dall'uso della parola necessitas, anche se, nuovamente, questa non s'identifica del tutto con la nostra 'necessità'; per esempio, Vitruvio afferma che le macchine sono necessarie perché senza di esse qualsiasi cosa può essere di impaccio (nulla res potest esse non impedita, X, 1, 3). In questo caso 'necessario' non individua ciò di cui non si può fare a meno, quanto piuttosto ciò che consente di ottenere un risultato con maggiore velocità e convenienza; la macchina rende più agevole la vita, ma non ne è un corredo indispensabile.
In alcuni trattati (Pseudo-Aristotele, Erone), la meccanica era indicata come fattore di miglioramento delle condizioni di vita del genere umano, o quanto meno come alleata dell'uomo nella sua lotta quotidiana contro una Natura poco amichevole, quando non decisamente ostile. Nella breve storia della meccanica delineata da Vitruvio (X, 1, 4), gli uomini invece sviluppano le macchine 'a imitazione' della Natura. In questo contesto le parole chiave non sono utilitas o necessitas, ma commoditas ed expeditio (con il suo opposto, impeditio, più spesso nella sua forma aggettivale impeditus). Le invenzioni da lui indicate come fondamentali sono necessarie, ma in un senso che distingue chiaramente tra esigenze primarie e desiderio di una vita che si è affrancata dal soddisfacimento di bisogni essenziali: il telaio produce vestiti, assolvendo alla funzione non soltanto di ricoprire e proteggere i nostri corpi, ma anche di adornarli in modo conveniente (sed etiam hornatus adiciat honestatem). Gli attrezzi per l'agricoltura ci consentono non soltanto di nutrirci e sopravvivere, ma anche di gustare la iucunditas del vino. La stessa iucunditas, in questo caso magna, è anche la reazione suscitata dalle risoluzioni di Archita di Taranto e di Eratostene di Cirene al problema della duplicazione del cubo, i cui risvolti pratici, specialmente per l'architettura, sono sottolineati da diversi autori (IX, praef., 14). Infine, bilance e altri strumenti per pesare tutelano gli uomini dalle frodi. Vi sono anche macchine la cui caratteristica precipua è di blandire i sensi dilettando vista e udito (si pensi alle fontane pneumatiche o agli automi di Erone). Tali macchine "non sunt ad necessitatem sed ad deliciarum voluntatem" (X, 7, 5) e fra esse Vitruvio dice di aver scelto le più utili e necessarie, rimandando alla lettura dei testi di Ctesibio chi fosse particolarmente interessato alla loro subtilitas (altra parola chiave, che corrisponde al gusto umano per le cose complicate). L'organo idraulico di Ctesibio, per esempio, su cui Vitruvio si sofferma a lungo a causa della sua complessità, è dotato sia di subtilitas, sia di curiositas (X, 8, 6). Quanto all'odometro, esso è stato prodotto dalla sollertia dei predecessori di Vitruvio (X, 9, 1), il quale associa ancora, nella sua descrizione, utilitas e delectatio (X, 9, 7).
Vitruvio inoltre è pronto a sottolineare che il valore reale di una macchina non sta tanto nella sua efficienza, quanto nell'ingegno umano che l'ha prodotta, che può comunque avere la meglio sulla macchina stessa qualora ve ne sia bisogno. La mēchanḗ suprema, per così dire, rimane pur sempre quella di Ulisse, l'individuo che con la propria astuzia sconfigge nemici ben più potenti. È in questa luce che si può leggere il celebre episodio dell'architetto Diogneto, che sconfisse il re Demetrio Poliorcete (e il suo architetto, Epimaco di Atene) con un semplice stratagemma, cioè una massa di fango, detriti e immondizie che, convogliati adeguatamente, impantanarono l'enorme helépolis (un tipo di torre da assedio) con cui il re voleva espugnare Rodi (X, 16, 3-8). Le innovazioni tecnologiche, ricorda Vitruvio, possono anche non funzionare, come dimostra il racconto di un certo Paconio, che decise di trasportare un blocco di marmo, da usare come base di una statua, non secondo un metodo tradizionale e ben sperimentato, ma utilizzando una nuova macchina di sua invenzione, giacché era bramoso di gloria (gloria fretus). Come era prevedibile, la macchina non funzionò perché non riusciva a mantenersi diritta sulla strada e quindi per ogni passo avanti ne faceva uno indietro (non si può fare a meno di ricordare il mito di Sisifo), cosicché l'architetto arrogante finì in rovina (X, 2, 13-14). Un modello che sembra efficace quando è costruito seguendo certe proporzioni può non funzionare se le proporzioni sono modificate; alcune cose, anche se prodotte su piccola scala, possono produrre effetti analoghi a quelli su grande scala; in altri casi è impossibile prevedere da un prototipo quali saranno gli effetti. Vitruvio sembra consapevole del fatto che, per quanto gli ingegneri fossero in grado di modificare le dimensioni di una catapulta in modo accurato, questo non voleva dire aver risolto tutti i problemi. Così, l'episodio di Rodi è seguito da altri analoghi in cui i consilia hanno valso più che i machinaria e la prontezza di riflessi e l'ingegno si sono rivelati l'arma migliore.
Questa e altre storie esemplari sono utilizzate per spostare l'accento dalle macchine a chi le adopera ed è interessante notare che, nella pagina finale della sua opera, Vitruvio finisca per incarnare i due tipi di conoscenza (scienza delle macchine e intelletto capace di contrastarle) nella figura professionale con cui egli stesso s'identifica e che cerca di promuovere con la sua opera, vale a dire l'architetto. Negli episodi da lui menzionati, le città furono liberate non dalle macchine ma 'contro' le macchine, dalla sollertia degli architetti (X, 16, 12). Come in Plinio, i 'tecnologi' sono portatori non soltanto di un particolare tipo di conoscenza, ma anche di determinati valori.
Frontino
di Serafina Cuomo
Sesto Giulio Frontino fu, secondo Plinio il Giovane, uno dei cittadini più rispettati della sua epoca. Ricoprì molte cariche di prestigio: prefetto di Roma, console (per tre volte), governatore della Britannia, augure e, nel 97 d.C., supervisore delle acque di Roma. Frontino offre un esempio molto interessante di 'ingegnere' non tanto per specifiche invenzioni o per conoscenze particolari, quanto per la chiara espressione che dà ai valori associati alla sua professione. Oltre a due libri di arte militare, di cui è rimasto quello degli Strategemata, e a un trattato di agrimensura, conservato parzialmente, egli è autore del De aquaeductu urbis Romae, che si presenta come un manuale scritto a uso proprio e dei suoi successori, e che comprende un catalogo ragionato di tutti gli acquedotti della città di Roma, con una descrizione della loro lunghezza e della loro origine, una breve storia della loro costruzione e del loro sfruttamento e una stima della loro portata. Frontino era responsabile non soltanto della manutenzione degli acquedotti e degli impianti idraulici dell'Urbe, ma anche di questioni connesse alla loro amministrazione e al controllo di abusi; le acque erano pubbliche ma avevano usi differenziati (le migliori come acqua potabile, le peggiori per irrigare orti o per il sistema fognario) e i privati per servirsene dovevano richiedere una speciale autorizzazione all'imperatore o ai suoi rappresentanti ufficiali. Frontino scoprì numerosi abusi sia nell'uso di certe acque per scopi non consoni sia nell'appropriazione indebita di acque destinate a tutti da parte di privati cittadini, spesso con la connivenza di pubblici impiegati.
Interessanti per il nostro discorso sono sia il modo in cui Frontino sostiene di aver smascherato tali abusi sia alcune delle misure preventive che egli escogita per evitarli in futuro. Usando calcoli più accurati di quelli dei suoi predecessori, egli confrontò la portata di ogni acquedotto (misurata in base alle dimensioni delle tubature) prima di entrare in città con quella al momento di entrare nei bacini di raccolta. In tutti i casi, la discrepanza fu tale da indurlo a concludere che l'acqua era in parte deviata abusivamente verso residenze private. Poiché non esisteva un'unità standard per tubature e giunture, non soltanto regnava il caos riguardo alla lunghezza dei condotti, al materiale adatto per le riparazioni e così via, ma era anche relativamente facile imbrogliare sul volume dell'acqua di fatto convogliata a privati, in quanto bastava usare tubature più grandi. Toccò quindi a Frontino tentare di stabilire una qualche forma di ordine e di controllo, fissando unità di misura a cui tutti si sarebbero dovuti adeguare, tanto nelle misurazioni quanto nelle erogazioni. Il rapporto tra la tubatura-base scelta, la quinaria, di diametro uguale a 5/4 di un dito (2,3 cm ca.), e i suoi multipli s'impone come standard, dice Frontino, sia perché facilita i calcoli e la manutenzione sia perché è raccomandato dall'imperatore (molto probabilmente Traiano) in un documento ufficiale; ratio e auctoritas vengono ad essere qui i fattori decisivi per la scelta. Nessuna grande invenzione, quindi, nessun espediente tecnologico particolare; anzi, Frontino cita un autore 'tecnico' solamente quando menziona Vitruvio come possibile inventore della quinaria. Il miglioramento nell'amministrazione degli acquedotti, che, come Frontino proclama con orgoglio, avrà conseguenze positive per l'intera città, è dovuto alla maggiore cura nel prendere misure, maggiore attenzione ai calcoli e all'imposizione di un ordine da parte della persona che ricopre l'incarico. Si ha quindi una corrispondenza tra efficienza tecnica e rettitudine morale; le due cose sono in un certo senso inseparabili e comportano anche un determinato atteggiamento nei confronti della gestione della conoscenza tecnica.
Tra i molti decreti del Senato romano che Frontino cita nella sua opera, alcuni risalenti a svariati anni prima, ve n'è uno che assegna un architetto 'd'ufficio' a ogni supervisore delle acque. L'entourage del funzionario include quindi esperti con competenze strettamente tecniche; non ci si aspetta che il supervisore degli acquedotti esegua di persona calcoli o riparazioni, che sono delegati al personale ‒ architetti o schiavi ‒ adibito a tali incombenze. Questo però non esime il supervisore stesso, sostiene Frontino, dall'avere conoscenza diretta della materia del proprio lavoro. Egli deve essere al corrente dei particolari specifici della sua materia in modo da poter esercitare meglio la propria autorità, e non dipendere da subalterni; questi sono sì necessari, ma in quanto strumenti, così come la mano è strumento della mente (con cui chiaramente Frontino stesso s'identifica, "quorum etsi necessariae partes sunt ad ministerium, tamen ut manus quaedam et instrumentum agentis", De aquaeductu urbis Romae, praef., 2). La forma di controllo cui si riferisce è ben esemplificata dalle mappe (formae) che egli dichiara di aver commissionato in modo da avere tutti i dettagli sotto gli occhi "et deliberare tamquam adsistentes" (I, 17).
Riassumendo, il ruolo supremo dell'ingegnere al servizio dell'imperatore (è importante ricordare che il beneficio è sempre presentato come rivolto all'intera popolazione, alla città in generale) è soprattutto quello di dirigere e imporre ordine, fermo controllo di fronte al caos (non soltanto materiale, ma anche morale) che altrimenti prenderebbe piede. Non si tratta soltanto di esercitare una funzione indispensabile alla collettività, sebbene il criterio dell'utilitas, presentata come beneficio per l'intera popolazione dell'Urbe, ricorra molto spesso. L'efficienza ha qui una decisa valenza politica; la storia degli acquedotti di Roma diventa un catalogo di Romani famosi, da imperatori a 'semplici' cittadini come Agrippa; il buon funzionamento del sistema idrico è indispensabile non soltanto per la salute degli abitanti dell'Urbe, ma anche perché Roma è la capitale dell'Impero e un esempio per il resto del mondo. La componente propagandistica dell'ingegneria romana trova forse una delle sue espressioni più esplicite quando Frontino esclama: "Paragona, se vuoi, a tante costruzioni necessarie, che trasportano tante acque, le vane piramidi o le altre inani ma celebri opere dei Greci" (Tot aquarum tam multis necessariis molibus pyramidas videlicet otiosas compares aut cetera inertia sed fama celebrata opera Graecorum, I, 16).
Sentimenti simili erano già stati espressi da Plinio il Vecchio: l'ingegneria non è un sapere fine a sé stesso, una forma di conoscenza del mondo neutra o 'passiva', ma un'attività umana impregnata di valori morali e politici, non ultimi la gloria e il potere dell'Impero romano.
La metrologia
di Pietro Dominici
Una parte importante della civiltà greco-romana è costituita dall'arte del costruire, che si sviluppa con continuità e con grande eccellenza in tutto il dominio spaziotemporale di quella cultura, dai grandi monumenti ateniesi dell'età di Pericle alle straordinarie realizzazioni urbanistiche, viarie e idrauliche nell'Impero romano. Subordinatamente, un ruolo primario in questa arte giocò la metrologia, come disciplina volta sia ai metodi per misurare grandezze rilevanti in quell'arte, quali lunghezze, superfici, volumi e pesi, sia alle procedure per fare conti con i risultati delle misurazioni, cioè con le misure. Per questo suo duplice aspetto, la metrologia greca, quella romana e poi, infine, quella greco-romana ebbero, come del resto si riscontra nelle altre civiltà, una forte interazione con varie esigenze pratiche della vita corrente, da una parte, e, dall'altra parte, con il mondo astratto dell'aritmetica e della geometria. è poi interessante il fatto che nel generale confluire delle due metrologie greca e romana si siano mantenuti, peraltro ben riconoscibili, alcuni caratteri propri dell'una e dell'altra.
Così, la metrologia greca, sviluppatasi inizialmente nell'ambito strettamente locale di ristrette comunità agropastorali, poi anche di commercianti, conservò a lungo questa caratteristica, in ciò differenziandosi fortemente dalle metrologie antiche dell'Egitto e del Vicino Oriente. Infatti, la rapida costituzione, in queste ultime regioni, di grandi regni portò all'omogeneizzazione non soltanto delle strutture organizzative della vita civile, ma anche delle normative che oggi chiameremmo 'tecniche' ‒ in esse incluse le tecniche di misurazione e le unità di misura ‒, in un ambito assai più vasto di quelli delle molte póleis, oltretutto mal comunicanti tra loro, che per gran parte dei tempi storici costituirono la Grecia antica. Il panorama generale delle unità di misura in uso nell'antica Grecia è quindi assai vario, ed è perciò un'operazione di difficile realizzazione e, tutto sommato, di dubbia utilità il cercare di tracciarne i lineamenti con una certa completezza. Peraltro, un momento unificante e, al tempo stesso, razionalizzante è riconoscibile nella riforma che Solone realizzò durante il periodo in cui fu arconte ad Atene (594-593) relativamente alle unità di misura in uso nella pólis ateniese e nelle sue colonie (particolarmente quelle nella Ionia dell'Asia Minore e nella cosiddetta Magna Grecia), nonché, estensivamente, nell'intera Attica e, genericamente, nelle regioni direttamente o indirettamente influenzate dalla cultura promanante da Atene. L'importanza che in prosieguo di tempo ebbero nell'intero mondo occidentale, in particolare in quello romano, le unità di misura derivanti dalla riforma metrologica ateniese di Solone, poi denominate 'misure attiche', si spiega facilmente pensando a quei potenti vettori di diffusione che per esse furono le opere filosofiche di Platone e di Aristotele, le opere teatrali di Eschilo, Sofocle ed Euripide, le realizzazioni degli architetti e degli scultori loro connazionali; non per nulla, queste unità di misura divennero di uso corrente, accanto alle precedenti unità autenticamente 'romane', nell'ambito della Roma repubblicana e ancor più nel successivo più ampio ambito del suo Impero. Per questi motivi ci limiteremo qui a dare notizie, tra le molte unità in uso nel mondo ellenico ed ellenistico, in maniera prevalente sulle unità di misura attiche, che, oltretutto, finirono col diventare le unità più usate in quel mondo. Accanto ad esse è da ricordare il particolare insieme di unità, di origine greca, formatosi in Egitto e nel Vicino Oriente, chiamate 'misure greco-egizie-romane' ma che, per aver avuto in Alessandria il centro massimo del mondo culturale che le espresse, appare più proprio denominare 'misure alessandrine'. Per completezza, la Tav. I e la Tav. II riportano le principali notizie sull'aritmetica greca e su quella romana, qui viste principalmente ‒ nello spirito di quello che è stato detto all'inizio di questo paragrafo ‒ come discipline attinenti ai modi usati dai Greci e dai Romani nel fare conti con i numeri costituenti misure.
Unità di misura attiche
È da osservare che, anche prima della conquista romana, alla denominazione greca di varie unità s'accompagnava spesso, equivalentemente, la denominazione latina, e di ciò v'è traccia diretta o indiretta (nelle denominazione italiana, derivata da quella latina) nelle tabelle qui proposte.
a) Unità di lunghezza. L'unità fondamentale era il piede (gr. poús), equivalente a 0,296 m, con vari multipli (specialmente per misure itinerarie) e sottomultipli, i più usati dei quali sono riportati nella tabella che segue.
Sono da notare due cose interessanti. La prima di esse, del resto comune ad altre unità simili sviluppatesi presso altre etnie, è la chiara origine antropica di alcune di queste unità, delle quali è onomastico il riferimento a parti del corpo umano (lo stesso piede, e poi dito, palmo, cubito, braccio) o a capacità specifiche motorie di esso (passo e doppio passo, intendendo per quest'ultimo il movimento che, partendo dalle gambe affiancate, porta ad affiancarle di nuovo muovendo in avanti prima una gamba e poi l'altra, cioè facendo due passi semplici consecutivi). La seconda cosa deriva dall'esame della colonna di equivalenza al piede nella detta tabella e consiste nell'altrettanto chiara influenza del sistema numerico sessagesimale degli Assiro-Babilonesi (multipli e sottomultipli di 60) e, in minore misura, del sistema pentadiadico degli Egizi (multipli di 5 e potenze intere positive e negative di 2); questa influenza ‒ per non dire parziale derivazione egizia e assiro-babilonese ‒ è testimoniata anche dalla presenza di alcune unità, per esempio il cubito, delle corrispondenti metrologie.
Prima della riforma di Solone era in uso ad Atene un piede leggermente più grande, di 0,328 m, denominato ‒ come altre unità riferite all'isola di Egina, attivissimo centro di commerci quasi fronteggiante Atene verso il Peloponneso ‒ 'piede eginetico'.
b) Unità di area di superfici. L'unità base era il piede quadrato, equivalente a 0,0876 m², e altre unità si formavano come quadrati dei succitati multipli e sottomultipli del piede; in particolare, nell'agrimensura le unità più usate erano la canna quadrata (100 piedi quadrati, 8,76 m²) e il pletro quadrato (10.000 piedi quadrati, 876,16 m²).
c) Unità di volume e di capacità. Si distingueva tra materiali solidi o aridi (per es. cereali) e materiali liquidi. Per i solidi e gli aridi, l'unità fondamentale era il medimno (médimnos), equivalente a 52,392 litri; essa aveva anche il valore ponderale di 52,392 kg ‒ il peso di un medimno (in volume) di acqua ‒, equivalendo a 120 volte l'unità attica di peso, la mina (436,6 g: v. oltre).
Per i liquidi, l'unità fondamentale era la metreta (metretḗs), equivalente a 39,74 litri. I sottomultipli più usati delle due unità citate sono indicati nelle tabelle seguenti.
d) Unità di peso. L'unità fondamentale era il talento (tálanton), equivalente a 26,196 kg, i cui sottomultipli principali sono indicati nella tabella che segue. Originariamente, era inteso come il peso trasportabile (in media) sulle spalle da un uomo e nei vari luoghi aveva diversi valori, sempre intorno a 25-35 kg; prima della riforma di Solone, il più usato era il talento eginetico, di 37,11 kg, e accanto alla mina da 436,6 g (detta allora 'mina leggera') era in uso anche una 'mina pesante' di valore doppio, cioè di 1/30 del talento di Solone, equivalente quindi a 873,2 g.
Queste unità ponderali avevano importanza speciale come unità monetarie se riferite a metalli pregiati (argento e oro); in particolare, la dracma (che tuttora è il nome dell'unità monetaria della Grecia) d'argento per le transazioni commerciali della vita comune e il talento d'argento per i grandi valori.
Unità di misura greco-egizio-romane, o alessandrine
Queste unità hanno spesso la stessa denominazione e gli stessi rapporti di multiplo e sottomultiplo delle corrispondenti unità attiche, salvo un differente valore intrinseco; esistono però unità nuove, in genere derivanti da unità romane, e per le unità omonime in vari casi è diverso da quello attico il rapporto rispetto all'unità fondamentale.
a) Unità di lunghezza. L'unità fondamentale è ancora il piede, ma con il valore di 0,350 m e, in epoca romana, 0,308 m, cioè rispettivamente 1,182 volte e 1,041 il piede attico di 0,296 m; la tabella che segue si riferisce al 'piede alessandrino' da 0,308 m. I nomi delle unità derivate e i rapporti reciproci sono quelli attici; per esempio, lo stadio era sempre di 600 piedi e valeva 210 m oppure 184,85 m in relazione ai detti valori del piede. Erano in uso anche unità di derivazione non attica; per esempio, un'unità pari a 8 stadi da 184,85 m, cioè col valore di 1479,9 m, detta mílion e derivata dal miglio romano (miliarium, di 1478 m).
b) Unità di area. Vale quanto ora detto per le unità di lunghezza.
c) Unità di capacità. Per gli aridi, il medimno ha un valore di 34,93 litri, che è 2/3 di quello attico; diminuisce in proporzione il valore dei sottomultipli di derivazione attica. A questi ultimi s'aggiunsero il modio (módios), pari a 1/3 di medimno (circa 11 litri) e tutta una serie derivante da una nuova unità, l'artaba (artábē), col valore prevalente di 29,11 litri; tra i sottomultipli esclusivi dell'artaba ricorderemo in particolare, per la sua origine romana, la libbra (lítra), fatta pari a 1/83,3 di artaba. Alcune di queste unità ebbero largo uso, sia pure con un valore leggermente differente, nella Magna Grecia e furono chiamate 'unità italiche'; per esempio, la libbra italica valeva 1/90 di artaba (0,323 litri). Queste unità avevano, come quelle attiche, anche valore ponderale con riferimento al peso del loro volume di acqua; per es., la libbra italica valeva 323 g. Per i liquidi, si usavano le unità attiche, però con la metreta che aveva un valore differente per i vari liquidi; per esempio, valeva 34,93 litri per l'olio e per l'acqua, ma 8,73 litri per il vino.
d) Unità di peso. La tabella che segue riporta quelle principali; come si vede, anche qui l'elemento caratteristico è il sostanziale mantenimento del sistema attico, arricchito di qualche unità nuova: centenario, oncia, siclo.
Unità di misura romane
Inizialmente, vale a dire nell'epoca dei re e anche nella prima fase della Repubblica ‒ diciamo fino a tutto il III sec. a.C. ‒ i Romani si servirono delle cosiddette 'unità latine' e 'unità italiche'; le prime erano di origine schiettamente locale, includendo l'apporto degli Etruschi, mentre le seconde erano le unità attiche ‒ sia pure leggermente variate nei valori ‒ usate dalle popolazioni largamente ellenizzate della Magna Grecia. è interessante notare che, ad onta della crescente penetrazione delle unità attiche, tanto più quando la Grecia entrò a far parte dei territori dell'Impero di Roma, i Romani non rinunciarono mai del tutto alle loro unità latine, tra le quali giova ricordare massimamente la libbra tra le unità di peso, e poi il quadrantale e i suoi sottomultipli per la capacità di liquidi, il passo (passus, precisamente, il doppio passo da 1,478 m) e il suo multiplo secondo 1000, il miglio (miliarum) per le misure itinerarie, lo iugero (iugerum) per l'area di superfici. Via via che si precisò e si estese l'ambito ‒ dapprima culturale e commerciale, e poi, in età imperiale, formalmente e sostanzialmente politico ‒ che noi oggi definiamo come 'greco-romano', l'uso generale delle medesime unità di misura portò anche a fenomeni di ridenominazione delle unità in questione, per i quali fu dato un nome romano a unità di origine greca e, viceversa, un nome greco a unità di origine latina. In questo senso va interpretata la doppia denominazione, greca e latina, che compare talora nel seguito per qualche unità.
a) Unità di lunghezza. L'unità fondamentale è, come nei sistemi greci, il piede (pes), che è esattamente il piede attico di 0,296 m della riforma di Solone (594-593), per le misure generiche e il doppio passo (passus) di 1,478 m per le misure itinerarie. Nella tabella seguente sono riportati i principali multipli e sottomultipli di queste due unità.
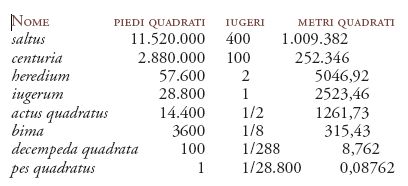
b) Unità di area di superfici. In un primo tempo, unità fondamentale fu per usi generici il piede quadrato (pes quadratus) e per usi agrimensori fu l'area di un quadrato di lato 100 piedi, lunghezza corrispondente all'unità attica pléthron, ridenominata versus; sul finire della Repubblica questo versus quadratus, pari a 10.000 piedi quadrati (876 m²), fu però sostituito, nel suo ruolo di unità agrimensoria di base, dallo iugero (iugerum), l'area di un rettangolo di 2×1 actus, pari quindi a 28.800 piedi quadrati. La tabella seguente indica le unità più usate e i loro valori.
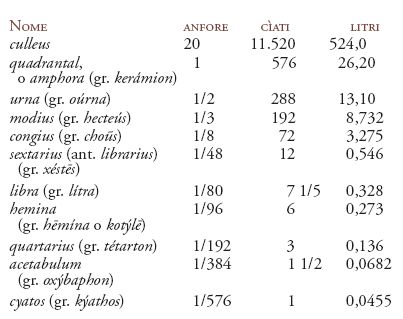
c) Unità di volume e di capacità. Erano sostanzialmente quelle attiche, a seguito di un adattamento di originarie unità latine; per esempio, il quadrantal era inizialmente il piede cubo (25,93 litri) e fu portato a coincidere, per i liquidi, con l'amphoreús greca (lat. amphora) col valore di 26,20 litri, diventando unità capostipite, come mostra la tabella seguente. L'unità fondamentale attica per solidi e aridi, cioè il médimnos, non fu però conservata, mentre lo fu la sua sesta parte, l'hekteús, che i Romani ridenominarono modius (moggio), sempre col valore di 8,732 litri. Come le corrispondenti misure attiche, le unità romane di capacità avevano anche valore ponderale, a partire dal valore di 8,73 kg per il modius (il peso di un modius d'acqua).
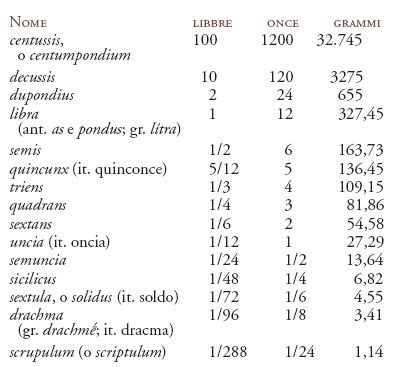
d) Unità di peso. Unità fondamentale era la latina libbra (libra, passata ai Greci come lítra, ma in antico si usò anche la denominazione pondus, da cui, più tardi, l'ingl. pound per l'unità ponderale e monetaria della Gran Bretagna), che circa a metà del IV sec. a.C. assimilò una precedente unità ponderale, lo as (asse) e circa a metà del I sec. a.C. fu assunta pari a 1/80 di talento attico, cioè a 327,45 g; la tabella che segue riporta i principali tra i numerosi suoi multipli e sottomultipli; tra questi, alcuni derivarono il loro nome dal pondus e dallo as (dupondius, per 2; tressis, per 3; quincussis, per 5; decussis, per 10; ecc.; semis, per 1/2; triens, per 1/3; ecc.); il sottomultiplo più importante della libbra era l'oncia (uncia), sua dodicesima parte e a sua volta divisa in molti sottomultipli introdotti per vari tipi di commercio e di artigianato. L'oncia e alcuni dei suoi sottomultipli avevano anche valore monetario, con riferimento al valore del peso corrispondente di argento o di oro.
Le unità di misura romane sopravvissero nell'ambito dei regni, delle signorie e dei domini che sorsero dalla dissoluzione dell'Impero, alcune restando in uso ufficiale fino a tempi recenti, cioè fino all'introduzione del Sistema metrico decimale (1875, inizialmente da parte di 17 Stati, tra cui l'Italia) e del successivo, più ampio Sistema internazionale SI (1960), che oggi è usato universalmente nell'ambito scientifico e tecnico e nella grande maggioranza degli Stati anche nella vita corrente; in quest'ultimo ambito fanno eccezione, nel senso di non avere esteso il Sistema internazionale alla vita ordinaria, quasi tutti gli Stati di lingua inglese (Gran Bretagna, ex Stati del Commonwealth britannico, ex colonie inglesi, Stati Uniti d'America e Stati culturalmente o industrialmente influenzati dai precedenti), lontana conseguenza della viva e tenace opposizione che al tempo della Rivoluzione francese e poi del primo Impero napoleonico gli Inglesi svilupparono contro tutto ciò che veniva dalla Francia ‒ compreso, poi, il Sistema metrico decimale e le unità di misura che ne derivarono ‒, presto cristallizzatasi in termini quasi irreversibili con lo stabilirsi dei primi standard della nascente grande industria britannica dell'Ottocento; è una singolare circostanza che in conseguenza di ciò sopravvivano ancora tranquillamente nella vita di tutti i giorni dei detti Stati, sia pure con valori leggermente differenti, unità di origine romana ‒ o, se si vuole, greco-romana ‒ quali il piede, il miglio, il piede quadrato, il piede cubico, la libbra, l'oncia e altre.
Bibliografia
Bussi 1985: Misurare la terra. Centuriazione e coloni nel mondo romano. Città, agricoltura, commercio. Materiali da Roma e dal suburbio, Ministero dei beni culturali, Soprintendenza archeologica di Roma, a cura di Rolando Bussi e Vittorio Vandelli, Modena, Panini, 1985.
Cambiano 1994: Cambiano, Giuseppe, Automaton, “Studi storici”, 35, 1994, pp. 613-633.
Diels 1914: Diels, Hermann, Antike Technik, Leipzig-Berlin, B.G. Teubner, 1914 (2. ed.: 1920).
Drachmann 1963: Drachmann, Aage Gerhardt, The mechanical technology of Greek and Roman antiquity. A study of the literary sources, Copenhagen, E. Munksgaard; Madison (Wis.), University of Wisconsin Press, 1963.
Ferrari 1985: Ferrari, Gian Arturo, Macchina e artificio, in: Introduzione alle culture antiche, a cura di Mario Vegetti, Torino, Boringhieri, 1983- 1992, 3 v.; v. II: Il sapere degli antichi, scritti di Giuseppe Cambiano [et al.], Torino, Boringhieri, 1985, pp. 163-179.
– 1985: Ferrari, Gian Arturo, Meccanica allargata, in: La scienza ellenistica, a cura di Gabriele Giannantoni e Mario Vegetti, Napoli, Bibliopolis, 1985, pp. 227-296.
Finley 1965: Finley, Moses I., Technical innovation and economic progress in the ancient world, “The economic history review”, 18, 1965, pp. 29-45.
Franco Repellini 1989: Franco Repellini, Ferruccio, Tecnologia e macchine, in: Storia di Roma, direzione di Arnaldo Momigliano e Aldo Schiavone, Torino, Einaudi, 1988-1993, 4 v.; v. IV: Caratteri e morfologie, 1989, pp. 323-368.
Gabba 1980: Tecnologia, economia e società nel mondo romano, a cura di Emilio Gabba, Como, New Press, 1980.
Gara 1994: Gara, Alessandra, Tecnica e tecnologia nelle società antiche, Roma, NIS, 1994.
Knorr 1989: Knorr, Wilbur R., Textual studies in ancient and medieval geometry, Boston, Birkhäuser, 1989.
Krafft 1996: Krafft, Fritz, Bemerkungen zur mechanischen Technik, “Technikgeschichte”, 33, 1966, pp. 121-159.
Landels 1978: Landels, John Gray, Engineering in the ancient world, London, Chatto & Windus, 1978.
Micheli 1995: Micheli, Gianni, Le origini del concetto di macchina, Firenze, L.S. Olschki 1995.
Oleson 1984: Oleson, John Peter, Greek and Roman mechanical waterlifting devices. The history of a technology, Toronto-Buffalo, University of Toronto Press, 1984.
Romano 1987: Romano, Elisa, La capanna e il tempio. Vitruvio o dell’architettura, Palermo, Palumbo, 1987. Schürmann 1991: Schürmann, Astrid, Griechische Mechanik und antike Gesellschaft. Studien zur staatlichen Förderung einer technischen Wissenschaft, Stuttgart, Steiner, 1991.
Soedel 1979: Soedel, W. - Foiley, V., Ancient catapults, “Scientific American”, 240, March, 1979, pp. 150-160.
Tomei 1982: Tomei, M.A., La tecnica nel tardo impero romano: le macchine da guerra, “Dialoghi di archeologia”, 4, 1982, pp. 63-88.
Traina 1994: Traina, Giusto, La tecnica in Grecia e a Roma, Roma-Bari, Laterza, 1994.
White 1984: White, Kenneth D., Greek and Roman technology, London, Thames & Hudson, 1984.