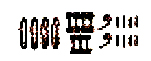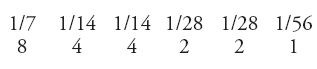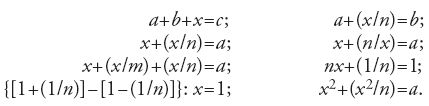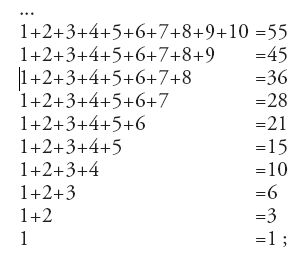Scienza egizia. Matematica

Scienza egizia. Matematica

Matematica

Nel mondo ellenistico, l'antichissimo, venerando e nondimeno meraviglioso Egitto era considerato la culla della scienza. Nel I sec. a.C. Diodoro Siculo scriveva, nel primo libro della sua Bibliotheca (I, 69), che gli Egizi sarebbero stati gli inventori non soltanto della scrittura, ma anche della geometria. Quattro secoli prima, Erodoto, il padre della storiografia, aveva visitato l'Egitto e aveva riferito (Historiae, II, 109) che sotto il re Sesostri per assicurare le imposte statali l'intero paese era stato lottizzato e che, dopo ogni straripamento del Nilo, i terreni, a causa dei cambiamenti subiti, erano subito rimisurati; in questo modo, secondo la sua opinione, era stata scoperta l'arte dell'agrimensura. Le nostre conoscenze confermano questa tradizione greca.

Le origini

di Walter Friedrich Reineke

L'Egitto è una delle aree del mondo antico in cui si sono riscontrati i primissimi segni di esistenza della matematica, o meglio, di una tecnica di calcolo. Gli albori si perdono nell'oscurità dell'epoca predinastica, precedente la scrittura, quando nella Valle del Nilo l'agricoltura era diventata un importante sistema economico, si erano sviluppati dei comuni rurali ed erano nati dei centri politici, quali le antiche circoscrizioni (nomoí). A capo di questi territori, i più antichi documentabili alla fine del IV millennio, erano posti i sovrani e i principi, con le loro corti di funzionari religiosi e laici. Essi ‒ come è chiaro sulla base delle testimonianze successive ritrovate in Egitto ed è anche verosimile se si considerano gli elementi forniti dall'etnologia ‒ riscuotevano le imposte dai villaggi, che garantivano la celebrazione dei riti rivolti agli dèi, il mantenimento della corte e l'organizzazione di lavori di interesse collettivo, come la costruzione di templi e di argini, o l'espletamento delle funzioni difensive.

A questo periodo risale la formazione di centri abitati nei quali risiedevano i sovrani e la loro corte, che possono essere considerati una forma antica di capitali. Un esempio documentato archeologicamente è l'insediamento di Ieraconpoli, situato 780 km ca. a sud del Cairo: su un'area di 2,5 km² si trovavano vasti spazi urbani formati da abitazioni rettangolari, l'area templare, quella palatina e diversi cimiteri. A partire dal 3300 ca. in poi può essere ricostruita la storia di queste aree, che continua anche in epoca dinastica sino all'inizio del III millennio. Per gli abitanti della Valle del Nilo la costruzione delle tombe regali (le più antiche delle quali sono state scoperte ad Abido, 550 km ca. a sud del Cairo, e a Saqqara) è stata una notevole impresa collettiva, basata su concezioni religiose. Per realizzare queste gigantesche costruzioni, fatte di mattoni ricavati dai sedimenti del Nilo, di legno e di canne, era indispensabile l'impegno collettivo di grandi masse di uomini. Il personale necessario proveniva dai villaggi, come per una sorta di leva al servizio della collettività, personificata dal sovrano, il quale fungeva da mediatore tra il mondo degli uomini e quello degli dèi.

La precisa costruzione ad angolo retto dei primi templi, dei palazzi e delle tombe regali mostra che si era in grado di misurare con precisione i terreni fabbricabili e di determinare gli assi degli edifici in base a un orientamento stabilito. Dovevano quindi essere noti i tratti caratteristici dell'agrimensura, dalla quale è nata la geometria. Inoltre, la raccolta dei tributi in natura nei diversi villaggi, sotto forma di alimenti per la corte e per le maestranze, oppure di materiali edili, l'immagazzinamento e la distribuzione di questi beni, ma anche l'organizzazione degli uomini nell'attività edile, presuppongono la disponibilità di una forma primitiva di tecniche di calcolo. È dunque in questo contesto che deve essere rintracciata l'origine dell'aritmetica. Partendo da questa constatazione, Diodoro Siculo (Bibliotheca, I, 81) racconta che i sacerdoti egizi, i detentori del sapere, avrebbero impiegato l'aritmetica solo per scopi pratici e come sussidio per la geometria, ma non per l'astrologia.

Tecniche di calcolo e sistemi di misurazione

di Walter Friedrich Reineke

I ritrovamenti effettuati nelle prime tombe regali hanno portato alla luce anche le prime testimonianze dell'uso della scrittura geroglifica e con essa i primi esempi di cifre egizie. Su una mazza cerimoniale del re Narmer (ca. 3050) si trova il numero 1.422.000 per indicare la quantità degli animali catturati. La grande quantità delle cifre scritte che proviene da quest'epoca deriva dalle iscrizioni o dalle note marginali ritrovate sugli oggetti lasciati nelle tombe, dovute alla pratica usuale nell'amministrazione di indicare per le forniture in arrivo il tipo di prodotto, la provenienza e la quantità.

Tav. I

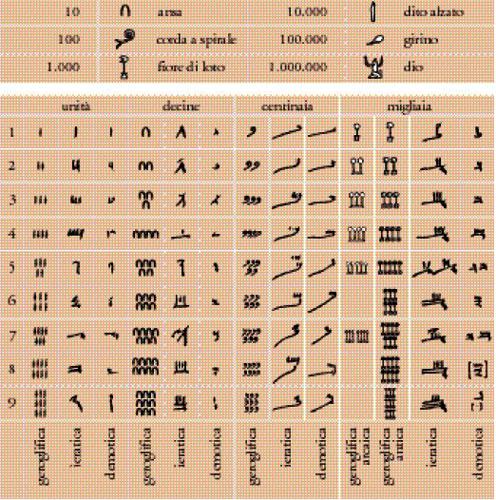
Questi antichissimi modi di scrivere i numeri mostrano un sistema numerico decimale pienamente formato (Tav. I).

fig. 1

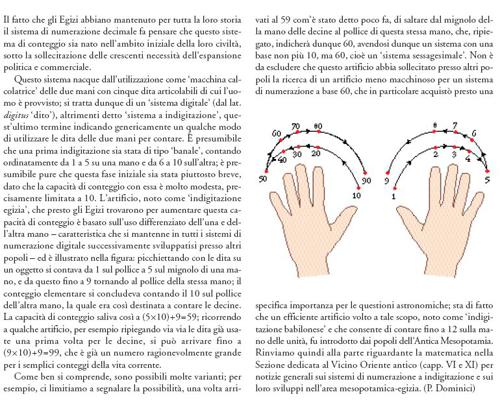
Gli Egizi usavano un particolare segno per ognuno dei numeri 1, 10, 100, 1.000, fino a un milione, vale a dire le potenze decimali da 10⁰ a 10⁶, e combinazioni additive di essi ‒ ben evidenti nella scrittura più antica, quella geroglifica ‒ per i multipli intermedi; per scrivere un numero intero tra due potenze decimali successive era usato il segno della potenza unitaria minore, ripetendolo poi quante volte fosse necessario e addizionando infine i valori dei segni, da leggere da destra a sinistra, come nella fig. 1, oppure nel senso opposto. Questi segni non avevano alcun valore posizionale né simbolico; la scelta corrisponde al criterio tipico del sistema di scrittura geroglifica (un ristretto elenco di segni grafici e un gioco di assonanze fonetiche).

L'addizione era la base dell'intera tecnica egizia di calcolo. Per esempio, sul monumento alla vittoria del re Khasekhemui (ca. 2750), il numero dei ribelli del Basso Egitto, che sono "sotto la pianta del piede del re", è indicato con la cifra 47.208, scritta usando i segni della fig. 1:

come dire (4×10⁴)+(7×10³)+(2×10²)+(8×10⁰). Come si vede, i segni numerici erano posti uno dopo l'altro secondo una sequenza decrescente delle potenze decimali e inoltre l'assenza di una di queste potenze (qui 10¹, quella delle decine) non era indicata poiché gli Egizi non conoscevano lo zero, né nella scrittura né nel linguaggio parlato.

Alla stessa epoca risalgono anche i primi documenti contenenti calcoli. Nei magazzini della piramide a gradoni di Djeser (2690-2670) giacevano migliaia di vasi di pietra, probabilmente provenienti dalle costruzioni funerarie dei predecessori di questo re, nell'interno di alcuni dei quali si trovano conteggi, scritti con l'inchiostro, relativi alla distribuzione delle razioni di pane o di cereali. La stessa disposizione di queste liste di calcolo in colonne e registri si ritrova nei grandi papiri contenenti conti di epoca successiva.

I magazzini della costruzione di Djeser contengono un'altra sorpresa. Alcuni recipienti sono provvisti di indicazioni di misure in palmi e in dita, unità metrologiche molto diffuse in epoca successiva, sottomultipli dell'unità fondamentale, il cubito. Queste misure sono state impiegate anche nella cosiddetta 'Pietra di Palermo' (la quale probabilmente era una copia di annali più antichi riportati per sicurezza su materiale imperituro) per indicare i livelli raggiunti nelle piene annuali del Nilo a partire dal 3000 ca. in poi. Nel sistema delle misure di lunghezza adoperato nell'intero Egitto faraonico, già pienamente sviluppato all'inizio del III millennio, l'unità fondamentale era il cubito appena ricordato, detto anche 'cubito regale' o 'cubito divino' e pari a 525 mm; 1 cubito era diviso in 7 palmi (di 75 mm) e 1 palmo equivaleva a sua volta a 4 dita (di poco meno di 19 mm); esisteva, ma era molto meno usato, un 'cubito piccolo', equivalente a 450 mm ca., diviso in 6 palmi (ognuno di 75 mm ca.) di 24 dita (da 3 mm ca. l'uno). Nelle indicazioni delle misure ricorrono alcune frazioni: 1/2, 1/3 e 2/3 sembrano certe. Dal moderno riesame delle misure sui recipienti e dall'analisi statistica delle dimensioni delle opere architettoniche, per la cui progettazione potevano essere usati soltanto multipli interi del cubito, si può desumere che il cubito regale fosse in uso già nell'epoca predinastica (3300-3050).

I dati numerici riportati a inchiostro sui vasi per l'olio o per i cereali mostrano che era stato sviluppato un sistema di misure di capacità, ben differenziato per i liquidi e per i cereali; tuttavia, a causa della precaria condizione dei documenti ancora non è stato possibile determinare quali fossero le unità di base. A partire dalla fine del IV millennio è stata attestata l'esistenza di pesi, in forma di piccoli parallelepipedi o di cilindri di pietra, per pesare i metalli e le pietre preziose. È stata trovata anche un'asta di pietra per pesare, riconducibile a quest'epoca. L'analisi statistica compiuta su una serie di campioni ha portato a individuare, quale base dei pesi di pietra, un'unità di misura di circa 27,5 grammi molto diffusa nell'Antico Regno.

Alcuni ritrovamenti (tavole da gioco, pedine), che risalgono all'epoca protodinastica e alle prime dinastie, relativi ai giochi cui si dedicava l'élite nelle ore di svago, offrono un ulteriore indizio dell'esistenza di una tecnica di calcolo; da testimonianze successive sappiamo infatti che i tiri per posizionare le pedine erano eseguiti con astragali, bacchette di löss o dadi e che era necessario eseguire dei calcoli mentali e delle combinazioni di numeri.

Sembra sicuro che il periodo di passaggio tra il IV e il III millennio, il quale portò all''unificazione delle Due Terre' (Egitto) e con essa allo Stato faraonico, fece maturare anche sviluppi decisivi per la formazione di tecniche di calcolo; la gestione delle imposte richiedeva infatti la registrazione dei dati numerici relativi ai prodotti in arrivo dalle terre amministrate e la conoscenza delle tecniche elementari di calcolo. Inoltre, l'attività edilizia aveva bisogno della logistica, del rilevamento delle superfici e dell'allineamento assiale degli edifici, nonché dell'armonizzazione delle dimensioni delle costruzioni in proiezione orizzontale e in sezione, e quindi di un sistema di misure. Lavori artigianali, come l'esecuzione di ornamenti a motivi intrecciati sulla base di un modello, comportavano addizioni e moltiplicazioni; anzi si potrebbero far risalire anche a questo tipo di attività le origini del metodo egizio di effettuare la moltiplicazione e la divisione attraverso raddoppiamento e decuplicazione (v. oltre). Si aggiunga anche lo scambio commerciale, che spesso avveniva su grandi distanze e comportava la misurazione delle quantità dei prodotti; lo sviluppo dei centri politici portò poi a una crescente standardizzazione dei sistemi di unità di misura. In definitiva, l'esercizio di attività professionali non sarebbe stato possibile senza una metodologia e senza un'aritmetica, le quali si sono sviluppate insieme, sotto le necessità imposte da una produzione che cresceva vertiginosamente e da un potere statale che s'andava allora affermando. Per quanto si può stabilire sulla base degli indizi conservatisi, in questo periodo esisteva, in forma embrionale, quasi tutto ciò che in seguito avrebbe caratterizzato la matematica egizia.

Con l'Antico Regno (2750-2190), la grande epoca in cui sono state costruite le piramidi, la matematica egizia deve aver trovato la propria forma definitiva. Non disponiamo però, per confermare questa congettura, di nessuno dei papiri che contenevano testi scientifici. Ci sono pervenuti i voluminosi archivi degli atti che provengono dai templi funerari dei sovrani della V dinastia, con l'elenco preciso delle entrate e delle uscite, nonché i protocolli delle consegne degli inventari dei templi; tuttavia non ci sono pervenuti resti dei manuali delle biblioteche dei templi o di altre istituzioni nei quali si aveva cura di raccogliere il sapere. Esistono comunque numerose testimonianze indirette dell'esistenza di nozioni matematiche, le quali però non sono ancora state raccolte sistematicamente e analizzate. È certo che la realizzazione di progetti statali di grande edilizia ‒ le piramidi, i templi funerari, le dighe, le strade e i canali, così come le spedizioni fuori dall'Egitto ‒ poteva essere garantita soltanto mediante un affinato sistema di riscossione delle imposte e di ridistribuzione del gettito, così come mediante l'impegno della popolazione per la realizzazione di queste imprese volute dal potere centrale. Tali imprese erano portate a termine grazie a uno studio logistico e sulla base di una tecnica di calcolo; i risultati possono essere tuttora ammirati nelle costruzioni, o in quello che di esse è rimasto.

L'esistenza di una notevole burocratizzazione nell'amministrazione delle imposte è attestata documentalmente; risalgono infatti alla metà del III millennio i papiri più antichi, non ancora pubblicati, con gli elenchi dei lavoratori, i conti delle vettovaglie, ecc. I prodotti agricoli e il bestiame consegnato dai comuni rurali che si erano ingranditi, oppure dai distretti amministrativi (nomoí) che erano stati fondati da poco con terreni misurati accuratamente, erano regolarmente censiti. Come alimenti di base erano immagazzinati soprattutto cereali, datteri e olio, per i quali gli Egizi possedevano un sistema di misura di capacità standardizzato e tarato.

Il cubito regale, o semplicemente cubito, di 525 mm, ricordato sopra, era la misura di lunghezza di base, dalla quale derivavano semplici unità frazionarie come 1/3, 1/4, 1/7 (il palmo, di 75 mm), 2/3 e 3/4. Sono indicativi, riguardo all'uso delle misure di lunghezza, i blocchi megalitici di precise dimensioni, i segni riportati sugli edifici e gli indici del livello delle piene del Nilo, oltre a un progetto di costruzione con l'indicazione delle misure per le varie parti. Per un quadro più completo della metrologia egizia si rinvia al paragrafo successivo, riguardante la matematica demotica. Anche il canone delle proporzioni che era seguito per realizzare le figure umane a tutto tondo e in piano si basava su misure di lunghezza e di area; la composizione delle scene è fissa, ossia esse sono poste una dopo l'altra in modo additivo, secondo un procedimento che era tipico di tutti i monumenti faraonici. Nell'architettura sembra sicuro l'uso della terna pitagorica, della sezione aurea e di quelle che ora chiamiamo successioni di Fibonacci. Se si aggiunge a questo l'elaborazione di un articolato sistema di misurazione del tempo, indispensabile anche per l'attività amministrativa, risulta indubbio che nell'Antico Regno si svilupparono le procedure e le caratteristiche fondamentali del sapere matematico egizio. Nessun periodo della storia faraonica avrebbe potuto favorire tante innovazioni per il superamento di seri problemi tecnici, quali quelli che si presentavano ai costruttori delle piramidi. Per trasformare in realtà le nuove idee occorrevano nuovi metodi di calcolo, mentre quelli già sperimentati furono migliorati. Il provare e lo sperimentare diedero luogo alle nuove conoscenze di cui aveva bisogno l'attività pratica.

Risalgono invece al Medio Regno (2000-1630) due chiare testimonianze che riguardano le procedure di calcolo degli Egizi e le loro conoscenze nell'ambito della geometria e della volumetria. Si tratta del papiro di Mosca (GMII 4676) e del papiro Rhind (papiro British Museum di Londra 10057 e 10058), entrambi compilati durante il Medio Regno, o poco più tardi, anche se ritenuti esplicitamente copie di un originale più antico; infatti nei testi sono presenti alcune caratteristiche linguistiche e particolarità grafiche che rendono probabile l'ipotesi della loro collocazione nell'Antico Regno. A questi ampi documenti si aggiunge anche una serie di frammenti, resti di ampi manoscritti dal contenuto matematico.

Tutti questi documenti non sono altro che raccolte nelle quali è esposto il sapere disponibile sotto forma di descrizioni di singoli casi; si tratta di testi orientati verso l'esperienza pratica, che non attribuiscono alcun valore all'indagine della legittimità delle procedure descritte. Tale modo di organizzare e di trasmettere il sapere è caratteristico dell'Antico Egitto e si ritrova anche nell'ambito della medicina, della veterinaria e dei testi magici; esso si ripropone ancora in testi demotici e giuridici nel III sec. a.C. La descrizione dei casi si sviluppa secondo lo schema seguente: "qualora si presenti questo e quest'altro problema" ‒ sono nominati esempi concreti ‒ "tu (lo scriba) devi operare così e così" ‒ seguono concrete istruzioni di calcolo ‒ "e troverai questo e quel risultato, tu (lo) hai trovato esattamente". Se sulla base delle testimonianze delle epoche precedenti era soltanto possibile dedurre quale fosse il livello di conoscenza raggiunto dagli Egizi, grazie a questi documenti è invece possibile identificare con chiarezza quali fossero le nozioni dei conti possedute dallo scriba.

Com'è stato accennato dianzi, alla base della numerazione e dell'aritmetica di epoca faraonica è l'addizione, sulla quale, a sua volta, riposa il principio della moltiplicazione e della divisione diadiche, cioè per 2 e suoi multipli. Ciò è già evidente dal modo in cui sono scritti i numeri. L'addizione e la sottrazione erano risolte in maniera banale, per lo più probabilmente attraverso calcoli mentali. La forma scritta, infatti, anche se era possibile, non era ritenuta necessaria neanche per i numeri più grandi e non è documentata se non per i calcoli con numeri frazionari.

Tav. II

La moltiplicazione era risolta attraverso diversi passaggi di tipo additivo. Analogamente si procedeva per eseguire la divisione (Tav. II). Le operazioni di elevare al quadrato e di estrarre radici sono documentate, anche se certamente erano scelti soltanto valori semplici e interi. Le potenze ‒ fino a 7⁵ (papiro Rhind 79) ‒ sono ricondotte a semplici passaggi additivi.

Una caratteristica particolare dell'aritmetica egizia è il complicato calcolo con numeri frazionari. Gli Egizi conoscevano, nella scrittura e nella lingua, soltanto frazioni unitarie, ossia frazioni con numeratore 1, a eccezione delle due semplici frazioni complementari 2/3 e 3/4. Nelle operazioni di calcolo, che probabilmente erano effettuate mentalmente, ogni frazione era scomposta in una serie di frazioni unitarie con denominatore crescente: x/n=(1/a)+(1/b)+…+(1/m), dove doveva essere a>b>…>m. Tali operazioni erano agevolate da tavole di scomposizione delle frazioni con numeratore 2 e denominatore dispari, contenenti i valori canonici che i buoni scriba tenevano a mente. Un'altra difficoltà per le operazioni con frazioni era il fatto che le suddivisioni dei sistemi di misura adoperati per i cereali (capacità) e per i campi (aree), fissati dalla tradizione, seguivano la serie di divisioni successive per 2: 1/2, 1/4, 1/8, 1/16, 1/32, 1/64. Anche a questo scopo ci si serviva di apposite tavole.

Nell'addizione e nella sottrazione di frazioni gli Egizi utilizzavano i cosiddetti 'numeri ausiliari', che servivano a ridurle a un denominatore comune e inoltre fungevano da sistema di controllo nei calcoli più complicati; si trattava quasi sempre di numeri interi oppure di frazioni semplici, soprattutto quelle della serie 1/2,…,1/64, ed erano utilizzati proprio nei casi in cui comparivano frazioni diverse da quelle delle serie di frazioni unitarie diadiche, decadiche o triadiche (vale a dire col denominatore costituito da un multiplo di 2 o 10 o 3). La frazione con il denominatore maggiore riceveva il numero ausiliare minore, di solito scritto in rosso. Per esempio, i numeri ausiliari nel problema 34 del papiro Rhind erano:

Gli Egizi erano in grado di risolvere semplici equazioni dei seguenti otto tipi (scritti con la notazione dell'algebra moderna, x indicando l'incognita):

In base alla loro complessità queste equazioni potevano essere risolte mediante una divisione diretta, oppure per mezzo della regola del tre semplice oppure grazie all'uso dei numeri ausiliari. Il problema di spartire una determinata quantità in parti uguali o disuguali (ax+by=c; y=nx) si presentava spesso nel corso del vettovagliamento di operai o di soldati. Quando la distribuzione doveva avvenire secondo una progressione aritmetica, era trattata in modo elementare, senza usare la formula della somma.

Anche il problema del calcolo dell'area di una superficie, che si ripresentava continuamente in ambito pratico, era padroneggiato bene. L'area A di una superficie rettangolare di lati a e b era calcolata secondo la formula A=a×b; quella di un trapezio di basi b, b´ e altezza h mediante la formula A=[(b+b´)/2]×h. Era anche possibile calcolare quali fossero le lunghezze dei lati di un rettangolo a partire dall'area, se era conosciuta la loro reciproca proporzione. L'area del triangolo rettangolo di lati ortogonali a e b era ottenuta con la formula A=(a/2)×b e anche in questo caso, una volta conosciuta l'area, era possibile individuare la lunghezza dei lati qualora se ne conoscesse il rapporto reciproco. In particolare, calcoli di triangoli ricorrevano anche nei problemi che riguardavano le piramidi. Anche i calcoli relativi al cerchio erano consueti per gli Egizi, i quali usavano un'approssimazione piuttosto buona per il fattore (il numero π) necessario per calcolare l'area del cerchio e la lunghezza della circonferenza, vale a dire 3,16, a sua volta approssimato come 4×(8/9)². Il problema 48 del papiro Rhind mostra che essi erano giunti a questo valore inscrivendo un cerchio in un quadrato e confrontando le aree delle loro superfici. Il lato del quadrato (che corrisponde al diametro del cerchio) è in questo esempio 9 unità; la superficie del quadrato può essere divisa in 81 piccoli quadrati, 64 dei quali erano ricoperti dalla circonferenza. Si pensa che nelle misure della lunghezza dei lati delle piramidi possa essere riscontrata la presenza del fattore π, che non ha alcuna ragion d'essere; la spiegazione sta nel fatto che per misurare grandi lunghezze, quali erano appunto quelle dei suddetti lati, gli Egizi ricorrevano all'artificio di contare i giri che faceva un disco di legno del diametro pari a un cubito e portante un segno sulla periferia, fatto rotolare sulla lunghezza da misurare; poiché a un giro completo corrispondevano π cubiti, la lunghezza espressa in giri di tale disco, che potrebbe essere chiamato 'cubito circolare', portava in sé il detto fattore irrazionale.

Il volume di diversi solidi era calcolato esattamente ed espresso in 'cubiti cubi', vale a dire con riferimento al volume di un cubo di lato un cubito (0,1447 m³), oppure usando unità di misura di capacità. Il volume V del cubo, del parallelepipedo e del cilindro era ottenuto mediante la formula V=G×h, con G area della base e h altezza; quello della piramide era calcolato come V=G×(h/3); quello del tronco di piramide a base quadrata, con a e b lati delle due basi inferiori e superiori, e h altezza, mediante V=(a²+ab+b²)×(h/3). Infine, gli Egizi sapevano trovare l'area della superficie della semisfera di diametro d mediante la formula A=2×(8/9)²×d², che ‒ considerando il valore egizio per il fattore π ‒ corrisponde a quella ancora oggi usata.

Tutti gli esercizi dei testi matematici sono rigorosamente orientati verso un'utilizzazione pratica nel contesto dell'amministrazione statale e dell'edilizia. Le regole di calcolo o le formule matematiche non erano indicate esplicitamente e soltanto la disposizione complessiva degli esercizi mostra che gli Egizi conoscevano perfettamente tali regole; nella loro concezione, esse erano parti della Maat, il vero ordine regnante nella Natura e nella società, e quindi non necessitavano di una formulazione esplicita. Le tecniche e le teorie di calcolo disponibili erano sufficienti a soddisfare le esigenze pratiche; la loro effettiva utilizzazione è evidente nella costruzione di opere gigantesche, quali le grandi piramidi, gli argini e i canali per regolare l'approvvigionamento d'acqua nel Fayyum e le poderose fortificazioni in Nubia. Infine, un capolavoro dell'agrimensura che può essere citato è la misurazione del Delta e della Valle del Nilo, alla quale si fa riferimento per la prima volta nella cosiddetta Cappella bianca di Sesostri I a Karnak (1956-1910).

Le conoscenze matematiche contenute nelle raccolte matematiche del Medio Regno (la cui conservazione sembra essere dipesa soprattutto dal caso) erano disponibili in realtà già dalla metà del III millennio. L'abbondanza delle testimonianze scritte databili al Nuovo Regno (1540-1076) o, meglio, la grande quantità che si è conservata, non apporta numerose novità alla storia della matematica. Voluminosi conti amministrativi e catastali testimoniano che le operazioni di calcolare, misurare, pesare e registrare si collocano a un livello paragonabile a quello dell'odierna burocrazia. La tecnica di calcolo in questo periodo migliora via via, ma non sembra che siano state ottenute nuove conoscenze. Degno di menzione è il papiro Anastasi I (1280), una lettera satirica in cui uno scriba viene messo a confronto con la sua conoscenza (o la sua ignoranza). Tra le questioni e i problemi posti, se ne trovano anche di tipo matematico, quali il calcolo dei viveri per i lavoratori che devono scavare un lago, il calcolo dello spostamento della terra e della quantità di laterizi per la costruzione di una rampa, la determinazione del peso di un obelisco per stabilire il numero degli operai necessari al suo trasporto e il calcolo dell'approvvigionamento per una spedizione militare in Siria. Problemi di tutti questi tipi erano già noti nei documenti del Medio Regno.

Il Nuovo Regno rappresenta il periodo imperiale della storia faraonica, durante il quale è allacciato un più stretto contatto, pacifico o bellicoso, con il litorale siro-palestinese, con l'Anatolia e con la Mesopotamia, i centri culturali più significativi nel mondo di allora. Il patrimonio di idee proveniente dall'Asia Minore, particolarmente nell'ambito della tecnologia, trova così uno sbocco nella Valle del Nilo. Tuttavia, da questa simbiosi non sono scaturiti consistenti impulsi per lo sviluppo della matematica, tanto è vero che gli Egizi hanno continuato a calcolare e a misurare sulla base dei loro metodi tradizionali; per esempio, non vi è alcuna testimonianza che essi abbiano ripreso o messo in pratica quei procedimenti per la risoluzione delle equazioni quadratiche, come il teorema di Talete o quello di Pitagora, già ben noti nella Mesopotamia del II millennio.

Dopo il Nuovo Regno, vennero a mancare gli impulsi interni a un ulteriore sviluppo della matematica, visto che, per quanto ne sappiamo, il livello di conoscenze raggiunto precedentemente era sufficiente a soddisfare le esigenze pratiche. Soltanto negli ultimi secoli a.C., sullo sfondo di una progressiva grecizzazione, diviene chiara la tendenza a preservare il sapere più propriamente egizio, di tipo sacerdotale. Ciò che si trovava nelle biblioteche dei templi e che era ritenuto degno di nota ‒ dagli inni e dai testi mitologici fino agli onomastiká, come le liste di lemmi di un'enciclopedia egizia ‒ era riportato in ieratico, la scrittura 'sacra'. Poiché invece ci sono pervenuti alcuni testi matematici scritti nel III sec. a.C. in demotico, che era la scrittura e la lingua della vita quotidiana, è possibile concludere che la matematica era considerata uno strumento delle attività pratiche di tipo corrente.

La matematica egizia antica, le cui origini risalgono alla fine del IV millennio e il cui sviluppo può essere seguito quasi senza lacune sino alla fine del II millennio (epoca a partire dalla quale, fino al IV-III sec. a.C., si apre invece una lacuna nella tradizione, la quale riprenderà poi con la matematica demotica), rappresenta un sistema unitario, formatosi all'interno dello stesso Egitto, di metodi per la risoluzione di problemi riguardanti le relazioni quantitative e i rapporti spaziali emergenti dalla realtà oggettiva. La matematica egizia antica rappresenta dunque un primo stadio dello sviluppo scientifico, nel quale la raccolta dei dati empirici, l'analisi di essi e la sperimentazione in vista della risoluzione dei problemi, così come la sistematizzazione del sapere, erano prioritari rispetto a una programmatica ricerca della conoscenza e della formulazione di leggi.

La matematica demotica

di Friedhelm Hoffmann

I testi demotici di matematica ‒ dove il termine 'matematica' va inteso nella sua accezione più ampia ‒ nella maggioranza dei casi proseguono la tradizione egizia più antica, anche se è possibile riscontrarvi una serie di innovazioni, in parte riconducibili a influssi stranieri. La funzione più importante della matematica demotica è stata quella di fungere da tramite nella trasmissione dell'antico patrimonio di conoscenze orientali ai Greci e, quindi, all'Occidente. I testi che ci sono pervenuti risalgono sia all'epoca tolemaica sia a quella romana. Accanto alle notevoli raccolte su papiro di scritti che possono essere considerati veri e propri lavori scientifici, a volte molto ricchi, si conserva un gran numero di testi di varia natura, dove si riscontra l'uso delle diverse tecniche aritmetiche. Si tratta di conti, ricevute, elenchi e altri documenti stilati dall'amministrazione statale e da quella religiosa, oppure di scritti che rientravano nella sfera privata, conservati su papiro, graffiti o óstraka. Sebbene queste fonti non rivelino niente di nuovo sulle conoscenze della matematica demotica, dimostrano che, in linea di principio, non vi era alcuna differenza tra le procedure di calcolo utilizzate nella vita quotidiana e quelle seguite nelle scuole dei templi: non esistono, dunque, elementi che autorizzino l'ipotesi di una scienza 'superiore' che fosse appannaggio della classe sacerdotale.

Il testo di matematica demotica più completo che ci sia pervenuto è una raccolta di esercizi scritta sul verso di una collezione di leggi. I quaranta esercizi, che risalgono approssimativamente al III sec. a.C., sembrano ordinati in base al grado di difficoltà, a partire dal più semplice, anche se mantengono un criterio tematico (Parker 1972). Poiché in questa raccolta, concepita come libro di testo, sono indicati l'ordine degli esercizi, le soluzioni e le prove, essa è particolarmente adatta a studiare la matematica demotica e la sua specifica terminologia. Come nella matematica egizia più antica, non si era soliti formulare delle regole generali; era inoltre sconosciuto il calcolo con le variabili e di regola si lavorava sulla base di un esercizio concreto e con dati numerici particolari.

Sistema numerico e metrologia

Il sistema numerico demotico non mostra differenze sostanziali rispetto a quello delle scritture più antiche. Come in precedenza, è usato un sistema decimale ma non posizionale, nel quale per ciascuna unità, decina, centinaio, ecc., esiste una cifra apposita (v. precedente fig. 1); lo stesso accade per singole frazioni numeriche, per frazioni di unità di area, per i numeri che servono a indicare le date e per le unità utilizzate per misurare quantità di grano. Non sono attestati numeri negativi. Le espressioni in uso per indicare lo zero non hanno un particolare significato nella tecnica aritmetica, poiché il sistema numerico egizio non conosce un metodo di scrittura posizionale delle cifre. La principale innovazione attestata nelle fonti demotiche è l'uso di frazioni proprie. Si suppone che i calcoli con i cosiddetti numeri ausiliari della matematica egizia, sopra ricordati, abbiano alla fine portato all'elaborazione di nozioni corrispondenti a quelle di numeratore e denominatore, anche se hanno continuato a restare in uso le frazioni unitarie e quelle complementari.

Il sistema di misurazione dei testi demotici è chiaramente semplificato rispetto al sistema di epoca faraonica, poiché le misure sono collegate più strettamente le une alle altre. Come è stato detto in precedenza, la base delle misure di lunghezza è il cubito, o cubito reale o cubito divino, pari a 525 mm ca., dal quale sono dedotte tutte le altre: 1 cubito (mḥ-nṯr)=7 palmi (šp), di 75 mm ca. ognuno; 1 palmo=4 dita (ḏb^c), di 18,8 mm ca. ognuno. Per lunghezze relativamente grandi era usata la 'fune di misurazione' (h̠-nwḥ) pari a 100 cubiti, ossia pari a 52,5 m ca., mentre per misure itinerarie era usato l''iteru' (ı̓trw), poi detto anche 'miglio egizio', pari a 20.000 cubiti, vale a dire 10,5 km ca.

Dal cubito sono dedotte anche le misure dell'area di superfici: 1 'cubito di terreno' (mḥ-itn)=100 cubiti quadrati=27,56 m² ca.; 1 arura (stʒ)=1 canna quadrata =10.000 cubiti quadrati =2756 m² ca.=0,2756 ettari ca.

Anche le misure di capacità derivavano dal cubito: 1 cubito cubico (144,7 dm³ ca.)=343 palmi cubici (hı̓n) pari a 0,422 dm³ ca. ognuno. Per i cereali sono però adottate misure non omogenee: 1 artaba (rtb)=28 o 29 o 30 o 40 choínikes oppure=64 hı̓n; 1/12 artaba=1 mḏ^ct. Inoltre, vasi e brocche di vario tipo e di varia capacità erano usati come unità di misura dei liquidi e anche degli aridi.

Per quanto riguarda i pesi, unità fondamentale era il deben (tbn), pari a 91 g ca.; seguiva il multiplo talento (krkr), pari a 300 deben, ossia a 27,3 kg ca. In particolare, per le misure di peso riguardanti le monete e i metalli preziosi, sulle quali si basava anche il sistema monetario tolemaico, l'unità fondamentale era il kite (qt, pari a 1/10 di deben e quindi pari a 9,1 g ca.); seguiva: 2 kite=1 statere=4 dracme=24 oboli. Tuttavia, nel corso del tempo la materia e i pesi, e quindi il valore, delle monete in Egitto furono ripetutamente ritoccati attraverso apposite riforme.

Aritmetica e geometria

L'addizione e la sottrazione erano normalmente risolte in modo banale; per lo meno, nei documenti pervenutici non vi sono indizi di tecniche particolari per i casi più complessi. Era invece applicato il tradizionale procedimento egizio diadico per la moltiplicazione e per la divisione (scomposizione in addizioni di sequenze di raddoppiamento o di dimezzamento), per il quale si rimanda a ciò che è stato detto nel precedente par. 2. I Greci designavano questo procedimento, con il quale erano elegantemente aggirate certe difficoltà del sistema numerico, come 'calcolo egizio'. Nel Medioevo esso continuava a essere insegnato come duplatio (raddoppiamento) ed è in parte rimasto in uso fino quasi ai tempi nostri. V'è un caso, in un papiro matematico demotico, in cui compare, a scopo di esercitazione, il procedimento greco, che era notevolmente più complesso.

In un papiro della tarda epoca tolemaica (Parker 1959) sono trattati sistematicamente, e con cifre diverse, alcuni esercizi che si risolverebbero modernamente come equazioni lineari con un'incognita, e che corrispondono ai calcoli-^cḥ^c del Medio Regno. Per esempio, uno dei problemi è enunciato così: "Che cos'è ciò alla cui metà va sommato 3 e al cui terzo 3, affinché ci dia il risultato 10?". Come già detto, in Egitto non esisteva la possibilità di annotare un'incognita nel calcolo, ma in termini moderni questo problema consiste nel risolvere l'equazione (x/2)+3+(x/3)+3=10. La procedura utilizzata corrisponde a trasformare l'equazione in (5/6)×x=4, risolvere (5/6)×y=1, ossia ottenere il valore inverso di (5/6), e infine moltiplicare il risultato per 4, per ottenere il valore cercato; questo valore finale, che è 4+(2/3)+(1/10)+(1/30), è sottoposto a verifica mediante una prova.

fig. 5

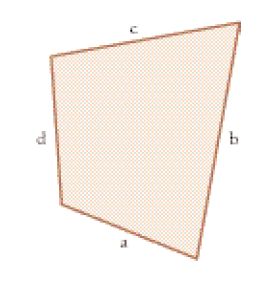
L'area delle superfici rettangolari, trapezoidali e triangolari era calcolata correttamente, come s'è detto nel precedente par. 2; così risulta, per esempio, in un papiro di Heidelberg (Parker 1975) per quanto riguarda un trapezio. Le aree dei quadrilateri irregolari, che si ritrovano in molti casi concreti (per es., negli appezzamenti di terreno: fig. 5), erano calcolate mediante la formula (a+c)/2×(b+d)/2, essendo a, b, c, d le lunghezze dei quattro lati; ne troviamo un esempio nel famoso elenco dei campi del tempio di Edfu, che è una versione geroglifica di un testo demotico (Meeks 1972).

Sono stati inoltre tramandati esercizi su progressioni aritmetiche nelle quali è necessario elevare un numero al quadrato; calcoli di questo genere erano concepiti come moltiplicazioni e pertanto non presentavano particolari difficoltà. È nota la formula corretta (n²+n)/2 per il calcolo della progressione 1+2+3+…+n, che dà luogo alla seguente rappresentazione:

è nota anche la formula, ugualmente esatta, [(n+2)/3]×[(n²+n)/2] per la somma 1+(1+2)+...+(1+2+...+n) complessiva per un dato n.

fig. 6

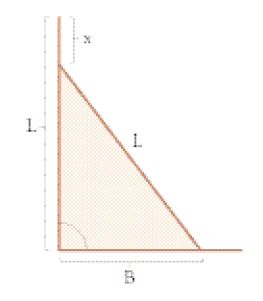
Particolarmente interessanti sono gli esercizi che presuppongono la conoscenza del teorema di Pitagora. Essi si presentano sotto una forma discorsiva: "un palo di una determinata lunghezza (L) sta appoggiato verticalmente a un muro; se la sua estremità inferiore è scostata dal muro di una certa distanza (B), bisogna calcolare di quanto (x) la sua estremità superiore si sia abbassata" (fig. 6).

Il fatto che nella Mesopotamia del II millennio, ossia molto prima di Pitagora (vissuto a cavallo tra il VI e il V sec.), fossero già attestati esercizi analoghi a questi, persino nella formulazione, rende verosimile l'ipotesi che vi sia stata una trasmissione delle conoscenze matematiche babilonesi all'Egitto. Per risolvere il problema appena formulato non sono sufficienti le operazioni di base addizione e moltiplicazione, e le inverse, nonché l'elevazione al quadrato, ma bisogna conoscere anche l'estrazione della radice. Per ottenere le radici di numeri che non sono quadrati perfetti si ricorreva alla formula di approssimazione che è attribuita a Erone di Alessandria: n^1/2=(a²±b)^1/2≈a±b/(2a). Erone di Alessandria però è vissuto solo nel I sec. d.C. e quindi la formula potrebbe essere stata una conquista elaborata in Mesopotamia, di cui probabilmente Erone potrebbe essere venuto a conoscenza attraverso la matematica demotica. Per i matematici egizi è del tutto chiaro che si trattava di una formula di approssimazione; infatti, nella prova il risultato era di nuovo elevato al quadrato e si annotava la differenza rispetto al numero di partenza.

La formula binomiale (a+b)²=a²+2ab+b² trovava applicazione negli esercizi relativi al calcolo dei lati di un rettangolo di cui fossero note l'area e la diagonale. Ricorrendo a metodi moderni, la risoluzione di tali esercizi è ottenibile mediante un sistema di equazioni a due incognite.

Nella raccolta di esercizi prima citata, occupano un posto di rilievo i calcoli relativi al cerchio, nei quali, al posto dell'antica approssimazione egizia di π≈(8/9)²×4≈3,16, si utilizzava il valore π≈3. Si tratta di un'approssimazione meno accurata, ma di più semplice applicazione, in uso anche presso i Babilonesi e molti altri popoli dell'Antichità per il rapporto tra lunghezza della circonferenza (c) e diametro (d) del cerchio; per l'area (a) si ha a≈(c/3)×(c/4) e d≈[(4/3)×a]^1/2. Queste formule trovano applicazione in diversi esercizi.

fig. 7

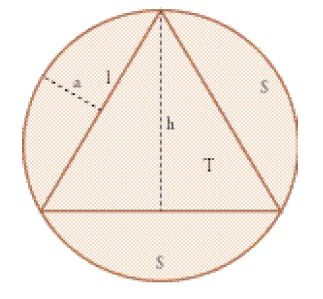
Il seguente problema, presentato in modo sommario nel papiro, può valere come esempio di un esercizio di geometria più complicato. Il problema è enunciato così (fig. 7): "[Sia dato] un terreno. Se [al] suo centro si trova un grande triangolo (equilatero) con tutti (?) e tre (?) i segmenti della lunghezza di 12 cubiti, qual è [allora] l'area del terreno? Guarda in che modo: [uno schizzo illustra il problema]" (Parker 1972, pp. 53-54). L'uso di disegni per illustrare gli esercizi geometrici risale ai più antichi papiri egizi di argomento matematico che ci siano pervenuti.

A scopo di esercitazione bisognava calcolare l'area complessiva risultante dalla somma dell'area dei tre segmenti circolari (S) e di quella del triangolo (T). Innanzi tutto si ricavava l'altezza (h) del triangolo in base al teorema di Pitagora: "Devi moltiplicare 12 per 12, che fa 144. Devi moltiplicare 6 per 6, che fa 36. Sottrai questo da 144 e resta 108. Estraine la radice [quadrata], che fa 10+(1/3)+(1/20)+(1/120). Questa è l'altezza media del solo triangolo". Il valore ottenuto era più accurato di quello che avrebbe dato la formula di approssimazione per la radice quadrata sopra citata. Quindi nel testo è calcolata l'area del triangolo: "Il numero [della] base [è] 12 cubiti, dunque [?] la sua metà 6, la sua altezza centrale 10+(1/3)+(1/20)+(1/120). Questa la moltiplicherai per 6, che fa 62+1/3+(1/60) cubiti. Questo è il numero [dell'area] del triangolo".

Infine, è calcolata l'area dei segmenti circolari. Nel papiro si dà per scontato che l'altezza (a) di un segmento circolare e l'altezza (h) del triangolo siano in un rapporto di 1:3, poiché infatti è indicato: "Devi prendere 1/3 [di] 10+(1/3)+(1/20)++(1/120), che fa 3+(1/3)+(1/10)+(1/60)+(1/120)+(1/180)". L'altezza del segmento circolare, calcolata correttamente, è inserita in una formula di approssimazione per il calcolo dell'area, che è data dalla semisomma dell'altezza (a) e della lunghezza (l) della corda, moltiplicata per l'altezza. L'uso di questa formula non tiene conto del modo in cui è stato ottenuto il segmento circolare e anzi è usata pure, per esempio, per calcolare i segmenti circolari che risultano da una circonferenza cui sia stato inscritto un quadrato. Nel nostro caso l'area del segmento circolare è approssimata come 25+(5/6)+(1/10) e l'area complessiva come 143+(1/10)+(1/20). Nella prova questa area è calcolata come quella di un cerchio il cui diametro si ottiene sommando l'altezza (a) del segmento circolare con quella (h) del triangolo. Il risultato è 144 e conferma quello precedentemente ottenuto con un altro procedimento.

Per quanto concerne la geometria dei solidi, si era in grado di calcolare volumi di piramidi in modo corretto. Un papiro conservato nel British Museum (Parker 1972, p. 53 e segg.) considera anche volumi di tronchi di cono, in linea di principio calcolati correttamente, sebbene π sia ancora approssimato a 3. In questo contesto è interessante sottolineare che fra le unità di misura di capacità d'uso, ve n'è una, hı̓n, che è definita geometricamente come 'palmo cubico', ricordato sopra.

Per concludere, si può affermare che la matematica demotica continua a rientrare per molti aspetti (sistema numerico, tecniche di calcolo) nella più antica tradizione egizia, pur sviluppandola sotto diversi punti di vista (frazioni proprie) e accogliendo alcune innovazioni derivate probabilmente dalla matematica babilonese. Nella scia della tradizione manca l'interesse per le dimostrazioni di carattere generale e i calcoli sono eseguiti con numeri concreti. Vi sono alcuni esempi in cui in un testo demotico si trova per la prima volta la risoluzione di un problema matematico tratto da un testo egizio più antico. Tuttavia, dal punto di vista della storia della scienza la matematica demotica è significativa soprattutto perché rappresenta l'anello di congiunzione con il mondo greco. Infatti, le tecniche della moltiplicazione egizia, il calcolo delle frazioni unitarie (per es., il calcolo onciale romano), il teorema di Pitagora o il procedimento di approssimazione delle radici quadrate, quindi in generale alcune delle tecniche aritmetiche, appartengono al patrimonio di conoscenze matematiche dell'Egitto trasmesso ai Greci attraverso la tradizione demotica.

Bibliografia

Andrews 1994: Andrews, Carol A.R., Unpublished demotic papyri in the British Museum, in: Acta Demotica. Acts of fifth international conference for demotists. Pisa, 4th-8th September 1993, Pisa, Giardini, 1994, pp. 29-37.

Badawy 1954-68: Badawy, Alexander, A history of Egyptian architecture, Giza, Studio Msr, 1954-1968, 3 v. [v. 2 e 3: Berkeley, University of California Press].

Becker 1966: Becker, Oskar, Das mathematische Denken der Antike, 2. durchgesehene Aufl. mit einem Nachtrag von Günther Patzig, Göttingen, Vandenhoeck & Ruprecht, 1966 (1. ed.: 1957).

Bernal 1967: Bernal, John Desmond, Die Wissenschaft in der Geschichte, 3. ed., Berlin, Dt. Verl. d. Wiss., 1967 (1. ed.: 1961; tit. orig.: Science in history, London, Watts, 1954; trad. it.: Storia della scienza, Roma, Editori Riuniti, 1956).

Borchardt 1922: Borchardt, Ludwig, Gegen die Zahlenmystik in der grossen Pyramide bei Gise, Berlin, Behrend, 1922.

Chace 1927-29: Chace, A.B. - Bull, L. - Manning, H.P. - Archibald, R.C., The Rhind mathematical papyrus, I-II, Oberlin (Ohio), Mathematical association of America, 1927-1929, 2 v.

Couchoud 1993: Couchoud, Sylvia, Mathématiques égyptiennes: recherches sur les connaissances mathématiques de l'Égypte pharaonique, Paris, Leopard d'Or, 1993.

Eisenlohr 1877: Eisenlohr, August, Ein mathematisches Handbuch der alten Ägypter [Papyrus Rhind des British Museum], übersetzt und erklärt von A. Eisenlohr, Leipzig, Hinrichs'sche Buchh., 1877, 2 v.

Gillain 1927: Gillain, O., La science égyptienne, l'arithmétique au moyen empire, Bruxelles, Fondation égyptologique reine Élisabeth, 1927.

Gillings 1982: Gillings, Richard J., Mathematics in the time of the pharaons, New York, Dover, 1982.

Iversen 1955: Iversen, Erik, Canon and proportions in Egyptian art, London, Sidgwick and Jackson, 1955.

Jürss 1982: Geschichte des wissenschaftlichen Denkens im Altertum, hrsg. von Fritz Jürss, Berlin, Akademie-Verlag, 1982.

Kol'man 1961: Kol'man, Arnost (Ernest), Istoriia matematiki v drevnosti, Moskva, Gos. izd-vo Fiziko-matematicheskoi lit-ry, 1961.

Loria 1946: Loria, Gino, Guida allo studio della storia delle matematiche: generalità, didattica, bibliografia; app.: "Questioni storiche concernenti le scienze esatte", 2. ed. rifusa ed aumentata, Milano, U. Hoepli, 1946 (1. ed.: 1916).

Meeks 1972: Meeks, Dimitri, Le grand texte des donations au temple d'Edfou, Le Caire, Imprimerie de l'Institut français d'archéologie orientale, 1972.

Neugebauer 1926: Neugebauer, Otto, Die Grundlagen der ägyptischen Bruchrechnung, Berlin, Springer, 1926.

‒ 1934: Neugebauer, Otto, Vorlesungen über Geschichte der antiken mathematischen Wissenschaften, Berlin, Springer, 1934; v. I: Vorgriechische Mathematik, 1934.

‒ 1969: Neugebauer, Otto, The exact sciences in antiquity, 2. ed., New York, Dover Publications, 1969 (1. ed.: København, E. Munksgaard, 1951; trad. it.: Le scienze esatte nell'antichità. In appendice: "Sulla decifrazione delle tavolette astronomiche dei caldei", Milano, Feltrinelli, 1974).

Parker 1959: Parker, Richard A., A demotic mathematical papyrus fragment, "Journal of Near Eastern Studies", 18, 1959, pp. 275-279.

‒ 1972: Parker, Richard A., Demotic mathematical papyri, Providence, Brown University Press, 1972.

‒ 1975: Parker, Richard A., A mathematical exercise - P. dem. Heidelberg 663, "Journal of Egyptian Archaeology", 61, 1975, pp. 189-196.

Peet 1923: Papyrus Rhind. The Rhind mathematical papyrus, British Museum 10057 and 10058, introduction, transcription, translation and commentary by Thomas Eric Peet, Liverpool, The University Press of Liverpool; London, Hodder & Stoughton, 1923.

Robins 1987: Robins, Gay - Shute, Charles, The Rhind mathematical papyrus: an ancient Egyptian text, London, British Museum Publications Ltd, 1987.

Sethe 1916: Sethe, Kurt, Von Zahlen und Zahlworten bei den alten Ägyptern und was für andere Völker und Sprachen daraus zu lernen ist: ein Beitrag zur Geschichte von Rechenkunst und Sprache, Strassburg, K.J. Trübner, 1916.

Struik 1972: Struik, Dirk J., Abriss der Geschichte der Mathematik, 5. Aufl., Berlin, Deutscher Verlag der Wissenschaften, 1972 (tit. orig.: A concise history of mathematics, New York, Dover publications, 1948, 2 v.).

Struve 1930: Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau, hrsg. und komm. von V.V. Struve, Transkription von B.A. Turajeff, Berlin, Springer, 1930.

van der Waerden 1956: van der Waerden, Bartel Leendert, Erwachende Wissenschaft, Basel, Birkhauser, 1956-1968, 2 v.; v. I: Ägyptische, babylonische und griechische Mathematik, 1956.

Vogel 1929: Vogel, Kurt, Die Grundlagen der ägyptischen Arithmetik in ihrem Zusammenhang mit der 2:n - Tabelle des Papyrus Rhind, München, Beckstein, 1929.

‒ 1958: Vogel, Kurt, Vorgriechische Mathematik, Hannover, Schroedel, 1958-1959, 2 v.; v. I: Vorgeschichte und Ägypten, 1958.

‒ 1974: Vogel, Kurt, Ein arithmetisches Problem aus dem Mittleren Reich in einem demotischen Papyrus, "Enchoria", 4, 1974, pp. 67-70.

Wussing 1962: Wussing, Hans, Mathematik in der Antike; Mathematik in der Periode der Sklavenhaltergesellschaft, Leipzig, Teubner, 1962.