Scienza egizia. Astronomia e calendari
Scienza egizia. Astronomia e calendari
Astronomia e calendari
L'astronomia egizia, confrontata con quella babilonese, appare fortemente arretrata. In realtà dall'Egitto ci è pervenuto un numero di testi astronomici molto minore di quello proveniente dalla Mesopotamia. Di fatto, a essere precisi, ci è giunto solo un tardo papiro (papiro Carlsberg 1) con la descrizione di fenomeni celesti piuttosto elementari, che oltretutto non sempre sono descritti in modo chiaramente comprensibile; soprattutto, a differenza della Mesopotamia, mancano gli elenchi di osservazioni (per es., delle eclissi) precisamente datati. Ciononostante, sembra abbastanza sicuro che debba essere esistita una maggiore quantità di annotazioni contenenti le osservazioni delle stelle e dei pianeti, così come gli elenchi delle eclissi solari e lunari e di altri vistosi eventi celesti (come le apparizioni di comete), ma che queste annotazioni, a differenza di quelle scritte in caratteri cuneiformi su tavolette di argilla, non si siano conservate a causa della poca resistenza e, allo stesso tempo, dell'alta deperibilità del materiale usato per scrivere (papiro). Inoltre, si è a conoscenza di titoli sacerdotali che indicano l'esistenza di persone con il compito di effettuare osservazioni astronomiche sul tetto del tempio durante la notte; poiché questi titoli sacerdotali sono stati in uso per un lungo periodo di tempo, si può ipotizzare che siano state compiute osservazioni del cielo per un periodo altrettanto lungo.
Sulla base del materiale rimasto è difficile, per non dire impossibile, farsi un'idea completa delle conoscenze astronomiche degli Egizi. Possiamo ricostruire la struttura del loro abituale calendario solare, ma già sulla questione dell'ulteriore presenza di un calendario lunare gli studiosi sono divisi. Sono inoltre noti due differenti tipi di orologi stellari, alcuni orologi solari e ad acqua, e una singola carta celeste, la cui interpretazione non è del tutto esente da contestazioni; in ultimo va ricordato, come fenomeno architettonico, l'orientamento astronomico di alcuni templi, nonché l'esatta disposizione verso nord delle piramidi dell'Antico Regno. Inoltre, alcuni testi egizi contengono rilevanti informazioni astronomiche in contesti diversi. Un buon esempio in proposito è rappresentato dal calcolo della lunghezza della circonferenza terrestre; come vedremo (par. 9), le cifre relative si trovano, in forma estremamente scarna e alquanto criptica, in un testo che descrive il viaggio notturno del dio Sole attraverso l'oltretomba, collocato in una tomba reale sigillata.
Calendario civile
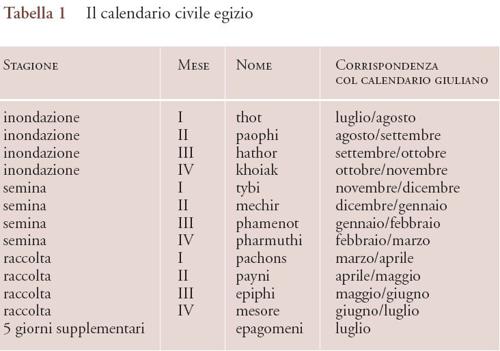
Il calendario egizio era costituito da tre stagioni di quattro mesi, ciascuno di 30 giorni, per un totale di 360 giorni, seguiti, alla fine, da cinque giorni supplementari, chiamati in egizio 'quelli che sono fuori dell'anno' e oggi per lo più detti 'epagomeni', secondo la denominazione greca. A partire dal Nuovo Regno (1540-1076), e soprattutto in epoca greco-romana (dal 332 a.C.), ogni mese ricevette un nome proprio, com'è descritto nella tab. 1.
Il primo giorno dell'anno era fissato in coincidenza con il sorgere 'eliaco', cioè in coincidenza con il sorgere del Sole, di Sirio, la stella fissa più luminosa, identificata dagli Egizi con una dea chiamata Spdt (Sothis per i Greci). A causa della sua posizione meridionale, Sirio risulta invisibile in Egitto da 55 a 70 giorni l'anno, a seconda del luogo e del secolo. A un certo giorno di metà luglio (del nostro calendario) riappare circa mezz'ora prima del sorgere del Sole, col quale inizia il giorno civile per il calendario egizio; mezz'ora più tardi di quel particolare sorgere di Sirio iniziava il primo giorno dell'anno. Questa era la struttura del calendario ideale al momento della sua introduzione. Poiché, però, l'anno egizio era più corto di quasi un quarto di giorno rispetto a quello naturale, sarebbe stato necessario inserire ogni quattro anni un giorno intercalare. Ciò, tuttavia, non fu mai fatto nella storia egizia; un tentativo tardivo in questa direzione, fatto in un sinodo di sacerdoti durante il nono anno del regno di Tolomeo III Evergete (238 a.C.), non ebbe successo. Non si conosce il motivo per cui gli Egizi rinunciarono a introdurre giorni intercalari; di sicuro non potevano ignorare la lunghezza reale dell'anno, visto che bastava rapportarsi a un evento astronomico fisso per far emergere l'errore nel giro di pochi anni. In proposito è stata avanzata l'ipotesi secondo la quale inserire un sesto giorno tra gli epagomeni sarebbe stato in totale contrasto con l'idea di simmetria propria degli Egizi, e la presenza di un giorno supplementare ogni quattro anni avrebbe distrutto l'ordine del calendario, basato su uniformità e regolarità complete. I giorni epagomeni erano collegati con la dea del cielo Nut, che generava ogni anno i suoi cinque figli appunto in quei giorni; sarebbe stato del tutto inaccettabile che essa generasse per tre anni i suoi cinque figli nei cinque giorni supplementari, e il quarto anno avanzasse un giorno in più. Dal mancato inserimento del giorno intercalare sono derivate due conseguenze, una per gli Egizi e l'altra per l'egittologia.
La prima conseguenza è che con questo calendario tutte le date si sarebbero spostate continuamente rispetto all'anno 'naturale', ossia all'anno scandito dall'alternarsi delle stagioni, mediamente di un giorno ogni quattro anni, il calendario effettivo e quello naturale venendo a coincidere soltanto ogni 1460 anni ca., una circostanza chiamata 'apocatastasi'; da questa situazione sarebbe derivato, in particolare, lo spostamento di tutte le date festive nel corso dell'anno naturale. Sembra però difficile ammettere, per esempio, che gli Egizi celebrassero una festa del raccolto, inizialmente fissata a un certo giorno di un mese estivo, quando, per il detto 'spostamento' del calendario rispetto alle stagioni, non era neanche cominciata la semina. Si può pertanto supporre che, almeno per alcune feste religiose, usassero un secondo calendario (che potremmo definire 'calendario civile idealizzato'), sebbene non sia dimostrabile la sua esistenza. In questo calendario ideale, valido soltanto per l'ambito religioso, il primo giorno dell'anno coincideva, com'è stato detto sopra, con il giorno immediatamente successivo al primo sorgere eliaco di Sirio, e tutti gli altri giorni erano fissati in riferimento ad esso.
L'altra conseguenza fu senza importanza per gli Egizi, ma è molto significativa per la scienza moderna. Poiché gli Egizi per ogni re cominciavano una nuova datazione e non ci è pervenuta nessuna lista completa di queste date, l'ordine cronologico assoluto risulta oscuro. Soltanto quando si riesce a individuare con certezza un evento astronomico menzionato contemporaneamente a una data egizia 'completa', vale a dire indicante giorno, mese e anno, allora si può calcolare la data assoluta con un'incertezza, nel migliore dei casi, di quattro anni. La cronologia egizia si basa appunto su quei pochi testi che contengono date di questo tipo.
Calendario lunare
L'esistenza di un calendario lunare egizio a sé stante costituisce una delle questioni più dibattute. Gli Egizi disponevano sicuramente di nomi per i singoli giorni del mese lunare (Parker 1950, pp. 11-12). In alcuni di questi giorni si celebravano feste religiose, mentre sino dall'Antico Regno (2750-2190 ) altri giorni (il 1°, 6°, 7° e 15°) svolgevano un ruolo speciale nel culto dei morti. Il mese lunare (lungo 29 o 30 giorni) costituì inoltre il modello per il mese del calendario civile (della lunghezza costante di 30 giorni), come testimonia il fatto che la parola egizia che significa 'mese' si scrive con un segno a forma di falce di Luna. Si può però parlare di calendario lunare soltanto se i singoli mesi hanno un nome proprio, oppure sono numerati da 1 a 12 (o 13) nell'arco di un anno; altrimenti, una numerazione a parte degli anni lunari non sarebbe affatto necessaria.
È difficile stabilire se un simile calendario sia esistito o no, in quanto non ci sono fonti certe al riguardo. Il papiro Carlsberg 9, che contiene una tabella di conversione valida per un ciclo di 309 mesi lunari (=9125 giorni=25 anni egizi di 365 giorni), risale difatti soltanto al 145-146 d.C. e riproduce una situazione del IV sec. a.C. Tutte le altre fonti dipendono largamente da interpretazioni e, in definitiva, le ipotesi sull'introduzione di un calendario lunare non hanno una vera e propria base testuale.
La teoria maggiormente accreditata negli ultimi decenni è quella di Richard A. Parker (1959, pp. 30-50), che suppone un calendario lunare originario introdotto tra il 2937 e il 2821. La regola per il mese intercalare era definita in modo da inserirne uno quando l'inizio del primo mese aveva luogo entro 11 giorni dopo il sorgere eliaco di Sirio poiché, in caso contrario, l'anno successivo Sirio non sarebbe più sorta nell'ultimo mese lunare. L'inizio dell'anno poteva così distare dal sorgere di Sirio da un minimo di 12 giorni a un massimo (con il mese intercalare) di 41 giorni. A causa della diversità della lunghezza dell'anno egizio rispetto a quella dell'anno naturale, Parker ha potuto inoltre calcolare il periodo di tempo assoluto in cui il calendario fu introdotto. Tale ricostruzione è stata in larga parte accettata, e soltanto la regola per il mese intercalare è diversamente definita dai singoli studiosi. Per esempio, Jürgen von Beckerath (Beckerath 1993, pp. 7-22, con un prospetto bibliografico) suppone un anno luni-stellare il cui primo mese cominciava col novilunio successivo al sorgere eliaco di Sirio e colloca il passaggio da questo calendario al calendario civile nel XXIX sec., in un anno nel quale il primo giorno di calendario civile coincideva con un giorno di novilunio (molto probabilmente il 2874).
L'esistenza di un simile calendario lunare che durante l'intera epoca dei faraoni avesse corso accanto al calendario civile, è contestata da Christian Leitz (Leitz 1991, pp. 54-57; Luft 1992, pp. 230-234). Questi suppone, per il periodo precedente all'introduzione del calendario civile di 360 giorni più i cinque epagomeni ricordato in apertura, un calendario di 365 giorni, il primo dei quali era definito con riferimento alla culminazione notturna di Sirio, la cui origine si colloca nel 3324 o 3323. Reminiscenze se ne possono osservare (Leitz 1995, pp. 104-106) sugli orologi decano-stellari del Medio Regno e sulla cosiddetta figura di Nut del periodo di Seti I (1295-1279 ca.).
Tabelle di conversione tra calendari diversi
Sul retro del papiro medico Ebers si trova un piccolo calendario di 13 righe che menziona contemporaneamente un sorgere eliaco di Sirio. Questo papiro gode della dubbia fama di essere, in considerazione della sua lunghezza, il testo dell'egittologia forse più dettagliatamente commentato; dalla sua scoperta, nell'Ottocento, gli egittologi gli hanno consacrato sicuramente più di 500 pagine, e la produzione di lavori a esso dedicati è ancora copiosa.
Nella prima riga questo calendario menziona il nono anno di regno di Amenhotep I (fine del XVI sec.); nelle successive 12 righe si trova una concordanza tra i nomi dei mesi e i mesi del calendario civile (simile a quella della tab. 1). Segue, in ogni riga, l'indicazione "giorno 9 del mese"; la riga accanto al primo mese contiene inoltre l'informazione lapidaria "sorgere (mattutino) di Sirio". La maggior parte degli studiosi riferisce i primi nomi ai mesi lunari; alcuni, tuttavia, non sono di questo avviso. Coloro che sostengono l'identificazione con i giorni del mese lunare ritengono il mese denominato "apertura dell'anno" l'ultimo; gli altri lo considerano il primo. La maggior parte degli egittologi individua nella seconda riga la menzione di un sorgere eliaco mattutino di Sirio nel nono giorno del terzo mese del periodo di raccolta, nel nono anno di Amenhotep I (1537). Sulla base di queste indicazioni, essi sostengono che si possa determinare l'anno assoluto del suo regno (di enorme significato per la cronologia egizia). Altri vi individuano la data di un'ascesa al trono. Poiché il sorgere eliaco di una stella dipende dalla latitudine geografica, i calcoli a ritroso hanno fornito come risultato date diverse, a seconda che il calcolo sia stato fatto per Menfi, Tebe oppure per Elefantina e che sia stato ammesso o no il legame con un giorno di novilunio. Infine, secondo un'altra tesi, il primo mese "apertura dell'anno" era fissato con riferimento al solstizio d'estate (in questo caso, il primo giorno del terzo 'mese di raccolta'), che all'epoca di Amenhotep I e alla latitudine di Menfi ricorreva otto giorni prima del sorgere contemporaneo di Sirio e del Sole (come già detto, il 'levare eliaco di Sirio'), il nono giorno del terzo 'mese di raccolta'. Il calendario sarebbe allora stato una tabella di conversione tra l'ordinario 'anno solare', basato sulla culminazione del Sole, e un anno 'di Sirio', basato sul primo sorgere eliaco di Sirio.
Orologi stellari
Gli orologi stellari più antichi risalgono al Medio Regno (2000-1630). Finora se ne conoscono 17 esemplari su sarcofagi di legno del periodo compreso tra la IX e la XII dinastia, vale a dire tra il 2140 e il 1780.
Uno schema può aiutare a comprendere come funzioni un simile 'orologio stellare diagonale'. Nella prima riga si trova la data, dalla prima decade (un periodo di dieci giorni) del primo mese fino all'ultima decade dell'ultimo. Alle 36 decadi che corrispondono ai 360 'giorni normali' dell'anno seguono i cinque 'giorni supplementari' o 'epagomeni'; sotto stanno altre 12 righe, la prima per la prima ora notturna, la dodicesima per la dodicesima. Nelle singole caselle ci sono i nomi di stelle che avanzano di un'ora a decade; il risultato grafico è una diagonale e da ciò deriva la denominazione 'orologio stellare diagonale'. La direzione del movimento è chiara, poiché tutte le posizioni delle stelle si spostano in avanti di quattro minuti scarsi al giorno. Una stella il cui sorgere un certo giorno indica la XII ora notturna raggiungerà così dieci giorni dopo la stessa posizione circa 40 minuti prima e, dal momento che, come si dirà oltre, un'ora egizia era di 40 minuti, indicherà di conseguenza la XI ora. Non possono qui essere approfondite le questioni relative alle ultime quattro colonne e alle stelle contrassegnate con la lettera maiuscola. In liste posteriori è assegnata, in analogia con Sirio, una durata di 'invisibilità' di 70 giorni a tutti i 'decani', vale a dire alle stelle fisse o costellazioni che servivano alla misurazione astronomica del tempo e che cambiavano ogni 10 giorni; è possibile indicare, sia pure in via schematica, una fascia di declinazione entro la quale tali decani dovevano trovarsi.
Questo è tutto quello che sappiamo con certezza sugli orologi stellari, sul resto non c'è unanimità tra gli egittologi. La prima e fondamentale questione consiste nello stabilire quale sia la posizione dei singoli decani. Le successive liste del Nuovo Regno (1540-1076) forniscono per ogni decano date relative a tre posizioni: (1) la culminazione all'inizio della I ora notturna (per culminazione s'intende il raggiungimento del punto più alto in cielo); (2) il tramonto eliaco (ultimo giorno di visibilità); (3) il sorgere eliaco (primo giorno di visibilità).
Alcuni studiosi basano i loro calcoli sul sorgere eliaco perché la posizione di Sirio alla XII ora della XVIII decade s'accorda con i dati archeologici e il sorgere mattutino di Sirio ricorre nella XVIII decade dal 2100 al 2060 ca., vale a dire, approssimativamente, all'epoca cui risalgono i sarcofagi. Ora, poiché, come ricordato all'inizio del capitolo, il sorgere eliaco di Sirio era decisivo per la determinazione del primo giorno dell'anno, sembrerebbe ovvio ritenere che costituisse il modello anche per gli orologi a decani. Sulla base di questa concordanza, gli studiosi ritengono inoltre che le date menzionate negli orologi stellari abbiano una validità relativa alla loro epoca di costruzione e che facendo ricorso ai periodi del sorgere eliaco di Sirio se ne possa determinare all'incirca la validità e, di conseguenza, il periodo di origine. Gli orologi stellari sarebbero stati soggetti a continui aggiustamenti e gli esemplari conservati rappresenterebbero soltanto stadi intermedi, risalenti fino al XXVIII o XXIX secolo.
Una serie di motivi s'oppongono tuttavia a quest'ultima ipotesi; i due più importanti sono quelli che seguono. Chi osserva il sorgere di una stella ha problemi nell'identificarla, soprattutto se si tratta, come nel caso dei decani, di stelle piuttosto deboli. Nel caso di stelle che ascendono diagonalmente, visibili ad altezze differenti a seconda delle condizioni atmosferiche, troverà spesso difficile decidere se una stella divenuta appena visibile sia davvero il decano cercato oppure una stella vicina; in molti casi potrà prendere la decisione definitiva soltanto dopo qualche tempo, quando anche le stelle vicine saranno sorte, circostanza che potrebbe limitare la praticabilità di un simile orologio ai fini del culto. Nel caso di stelle che tramontano, invece, non sussistono difficoltà del genere.
Dal punto di vista della teoria appena esposta, un orologio stellare diagonale non sarebbe più valido già dopo 40 anni; tuttavia, essendo collocato all'interno di un sarcofago, dovrebbe avere validità eterna, cosa che contraddice apertamente la prima osservazione. Assumendo l'ipotesi che l'orologio si basasse su stelle che tramontano, invece, il problema non sussisterebbe più. Come già detto, Sirio indica nella XVIII decade la XII ora notturna e, di conseguenza, la I nella XXIX. Se si tratta di un tramonto, alle indicazioni schematiche dei testi astronomici egizi seguono sette decadi di invisibilità fino al sorgere eliaco. La fase di invisibilità finisce al termine della XXXVI e ultima decade, vale a dire, poiché gli epagomeni non sono considerati nei testi astronomici, alla fine dell'anno. In altre parole, secondo l'ipotesi dei tramonti stellari, gli orologi stellari diagonali contengono un calendario ideale in cui l'inizio dell'anno è determinato attraverso il sorgere eliaco di Sirio. Tale calendario ha una validità eterna, cosa che s'accorda con la collocazione all'interno di un sarcofago.
Rimangono ancora altre questioni. Se si presume che l'orologio stellare contiene un calendario ideale, allora si perde ogni possibilità di determinarne l'epoca d'origine. Esso può risalire a qualsiasi periodo; può essere stato prodotto all'inizio del Medio Regno, il periodo cui risalgono le prime testimonianze relative a questi orologi, ma può anche essere stato concepito nell'Antico Regno. Le ore indicate attraverso le stelle dei decani sono lunghe 40 minuti (più esattamente, dividendo per i 365,25 giorni di un anno il prodotto di 24 ore per 60 minuti per i 10 giorni di una decade si ottiene il risultato di 39,425 minuti). Il decano di turno indica la fine di un'ora notturna all'inizio di una decade e l'inizio di essa alla fine della decade. Infine, l'ultima questione è stabilire se i decani fossero una o più stelle. Considerazioni pratiche fanno propendere per la prima ipotesi; chi desidera indicare esattamente l'inizio o la fine di una determinata ora opterà per un evento singolo, chiaramente definito, come il tramonto di una stella unica, e non per eventi numerosi che si succedono nel tempo, come i tramonti di stelle differenti.
È possibile identificare qualcuno dei decani disegnando approssimativamente su una carta gli orizzonti del tramonto per il cielo dell'anno, poniamo, 2100 a Menfi o in un'altra località dell'Egitto. Un'analisi completa e assolutamente sicura, tuttavia, è limitata da numerosi motivi. Chi costruisce un orologio stellare cercherà stelle che tramontano nello stesso momento a distanza di dieci giorni l'una dall'altra, oppure stelle che tramontano nello stesso giorno a distanza di circa 39,5 minuti (il risultato è lo stesso). Ora, anche se si avesse a disposizione un orologio moderno non si potrebbe costruire un orologio stellare preciso al minuto e, allo stesso tempo, di uso pratico. Solo raramente, difatti, tramonterà una stella anche soltanto discretamente luminosa proprio in questi intervalli, riferiti all'incirca al tramonto di Sirio. Il costruttore dovrebbe ripiegare su una stella più debole, e quindi spesso difficile da osservare, oppure dovrebbe fare determinate concessioni di tempo, fino al tramonto di una stella più luminosa. Attualmente non c'è alcuna possibilità di verificare come l'inventore dell'orologio stellare si sia comportato oltre 4000 anni fa nei singoli casi e già soltanto per questo motivo le ricostruzioni non possono essere adottate con sicurezza assoluta. Anche in condizioni ottimali, un orologio così strutturato non può aver comportato errori minori del 10-15% in rapporto alla lunghezza delle singole ore.
Orologi stellari ramessidi
Gli orologi stellari del Medio Regno (2000-1630) presentavano numerosi svantaggi. Il più grave, per un Egizio, consisteva sicuramente nel fatto che 12 ore decane, per complessivi 12×39,425=473 minuti, corrispondevano abbastanza bene a otto ore odierne, per complessivi 8×60=480 minuti. In Egitto questo sistema si adattava molto bene a una notte estiva di 10 ore odierne (600 minuti) e a crepuscoli di circa un'ora, ma in una notte invernale di 14 ore odierne, ben quattro non venivano rilevate dal computo del tempo. Ogni notte e ogni giorno (qui inteso come periodo di tempo dal sorgere al tramontare del Sole) duravano 12 ore indipendentemente dalla stagione e quindi una singola ora notturna era notevolmente più lunga in inverno che in estate. Due invenzioni dell'inizio del Nuovo Regno (1540) cercarono, in modo del tutto diverso, di porre rimedio a questa situazione insoddisfacente. Una è quella degli orologi ad acqua, di cui si dirà nel paragrafo seguente, e l'altra è quella dei cosiddetti 'orologi stellari ramessidi', con riferimento agli 11 faraoni di nome Ramesse. Di questi ultimi orologi si conservano quattro copie del periodo ramesside tardo (1150-1110), ma l'originale è più antico di 300-350 anni (Neugebauer 1964).
Il nuovo orologio stellare tiene conto della differente lunghezza delle ore notturne a seconda della stagione ed è anche adatto, in base alla sua impostazione, a consentire misurazioni notevolmente più accurate dell'orologio stellare basato sui decani. Il cattivo stato di conservazione delle quattro copie ha sicuramente fatto sì che il progresso tecnico rappresentato da questi orologi rispetto a quelli a decani sia stato a lungo disconosciuto e che, nelle prime storie della scienza, gli orologi stellari ramessidi fossero considerati il prototipo di una costruzione evidentemente sbagliata. Causa principale della scarsa considerazione di cui godevano era proprio l'originalità della loro struttura; semplicemente, la scienza moderna non poteva immaginare che un orologio così concepito potesse funzionare. È anzitutto opportuno darne una descrizione. Un orologio completo contiene 24 tavole, relative ogni volta al I e al XVI giorno di un mese egizio; gli epagomeni non sono menzionati a parte, ma è possibile che l'ultima tavola valesse per 20 giorni invece che per 15. Ogni tavola consiste di 12 strisce. La prima va dall'inizio della notte alla fine della I ora e la tredicesima va sino alla fine della XII ora. Ogni striscia contiene tre indicazioni: l'ora, il nome di una stella e l'indicazione di una posizione. Delle stelle, alcune appartengono a una costellazione, altre sono stelle singole; ne sono nominate complessivamente 46. Riguardo alla posizione sono possibili sette indicazioni diverse: spalla destra; orecchio destro; occhio destro; centro; occhio sinistro; orecchio sinistro; spalla sinistra. Queste indicazioni di parti del corpo fanno riferimento a una figura umana; poiché, accanto alla tavola vera e propria, le indicazioni di posizione sono nuovamente tracciate in un reticolo, i concetti di destra e sinistra vanno intesi sicuramente a partire dal punto di vista della figura, disegnata dentro oppure sotto ciascun reticolo.
La posizione centrale indica il meridiano, le altre contrassegnano stelle che si trovano a est o a ovest di esso (indicano cioè l'azimut). L'intero metodo di misurazione va probabilmente immaginato in maniera tale che la figura di riferimento sia posta esattamente a sud, mentre l'osservatore le siede di fronte a nord. Una stella è al culmine quando si trova sul meridiano locale; ciò significa che nella posizione di destra non è ancora al culmine (si trova a est del meridiano), mentre nella posizione di sinistra la culminazione è già passata (la stella si trova a ovest). Poiché una delle nominate stelle può essere identificata molto verosimilmente con la stella Rigel (β Orionis), attraverso le indicazioni della sua posizione è possibile stabilire l'anno di costruzione dell'orologio in modo abbastanza accurato: tale anno è intorno al 1460, come in una carta celeste trovata nella tomba tebana di Senenmut. Una volta noto l'anno di costruzione, si possono confrontare le date egizie con quelle giuliane e utilizzare queste ultime come base per calcoli ulteriori.
Una questione molto rilevante riguarda la lunghezza del crepuscolo negli orologi stellari. Riuscire in qualche misura a risolverla costituirebbe un grande progresso, in quanto con l'ausilio del giorno e dell'ora si può calcolare in qualsiasi momento l'ascensione retta delle stelle culminanti. Il problema appare a prima vista insolubile; infatti come si può sapere, non conoscendo le stelle, quando cominciava la I ora notturna (tramonto del Sole) o finiva la XII (sorgere del Sole)? Un esame ulteriore permette però di risolvere il problema, almeno entro certi limiti.
Un ausilio in proposito è dato da stelle che con la stessa posizione indicavano tanto l'inizio della prima ora quanto la fine dell'ultima, eventualità che ricorre più volte nell'orologio stellare. Il seguente esempio può spiegare il procedimento. Tra le due date angolari per una determinata stella nella posizione 'centro' intercorrono 140 giorni; in questo caso, si sa che una stella 140 giorni più tardi raggiungerà la stessa posizione (cioè la culminazione) e che il momento della culminazione si sarà spostato nel frattempo di 9,21 ore in avanti (corrispondenti a 140 giorni : 365 giorni×24 ore). Il tramonto all'epoca della prima data avveniva alle 17,93, l'alba, all'epoca della seconda, alle 5,09; la differenza tra i due momenti è di 11,16 ore. Durante 9,21 ore la stella doveva essere visibile in ogni caso; per i due crepuscoli mattutino e serale resterebbero allora in tutto 11,16−9,21=1,95 ore. Se si presuppone che le 12 ore notturne siano raggruppate più o meno simmetricamente attorno alla mezzanotte, vale a dire che il crepuscolo mattutino e quello serale siano di lunghezza pressappoco uguale, si può dividere 1,95 per due e si ottiene 0,975: circa un'ora per la durata del crepuscolo in considerazione nei due giorni. Questo metodo di calcolo può essere adoperato anche nel caso di un insieme di sette stelle, ottenendo per il crepuscolo una durata media di poco più di un'ora. Nell'epoca detta erano visibili in Egitto stelle fino alla quarta grandezza.
Un ulteriore problema è costituito da indicazioni di posizione come 'orecchio sinistro' o 'spalla destra', ritenute da quanti se ne sono occupati vaghe e inutilizzabili. A questo proposito non era stata sinora presa in considerazione la possibilità che il concetto di occhio sinistro potesse essere, per esempio, solo una cifra che designa una determinata distanza dell'azimut dal meridiano. Esempio paragonabile per l'uso di tali cifre nell'astronomia è un'indicazione come 'il pianeta Saturno sta nel Leone'. Si tratta anche qui di un'indicazione esatta, con cui s'intende che il pianeta Saturno in un dato periodo si trova tra 120° e 150° di longitudine celeste. L'unica differenza tra l'antica indicazione egizia 'orecchio sinistro' e 'il pianeta Saturno nel Leone' è che, nel secondo caso, la decifrazione è una pratica del tutto corrente (120°-150° di longitudine celeste), mentre non lo è nel primo.
Attraverso calcoli di prova e con l'ausilio di una carta celeste si possono determinare in buona parte le singole stelle e le indicazioni di posizione, riscontrando un'accuratezza media di circa 13 minuti per le quattro versioni mal tramandate; considerando solo il suo tipo di costruzione, un simile orologio potrebbe vantare una precisione di circa 5 minuti. Rispetto agli orologi stellari basati sui decani, il miglioramento decisivo nel sistema è rappresentato dal maggior numero di stelle utilizzate e, soprattutto, dal fatto che non viene più considerata soltanto una posizione (nelle stelle decane, il tramonto), ma sette posizioni diverse. Con un sistema di 46 stelle e 7 posizioni possono essere ricoperti 46×7=322 diversi punti del cielo rispetto ai soli 36 delle stelle decane; ciò costituisce l'autentico miglioramento di qualità degli orologi stellari ramessidi.
Orologi ad acqua
In questi dispositivi l'indicazione oraria era tratta dal livello dell'acqua in un recipiente dal quale l'acqua medesima defluiva ('orologi a deflusso'), oppure al quale affluiva ('orologi ad afflusso'), attraverso orifizi tarati; essi erano usati prevalentemente per le 12 ore notturne, in quanto per le ore diurne si preferivano i più semplici e più accurati orologi solari dei quali si dirà nel paragrafo seguente. Ha fama di inventore dell'orologio ad acqua un certo Amenemhat, vissuto all'inizio del Nuovo Regno sotto i re Ahmose e Amenhotep I (1550-1504 ca.). Il più antico orologio ad acqua conservato è stato rinvenuto a Karnak e risale all'epoca di Amenhotep III (1391-1353 ca.); la maggior parte degli appena 20 esemplari conservati datano tuttavia dopo il 600 a.C.
Degli orologi ad acqua che ci sono pervenuti soltanto uno, di epoca romana, è ad afflusso; tutti gli altri (abbastanza somiglianti tra loro) sono a deflusso e consistono in un vaso di pietra a forma di cono circolare tronco in basso, sulla cui parte esterna si trovano per lo più rappresentazioni delle 12 divinità dei mesi e delle stelle decane. Nella parte interna si trova una fila di misurazione per ognuno dei 12 mesi, ciascuna costituita da 11 tacche di deflusso poste, ad altezze differenti, al di sopra dei geroglifici che significano vita e durata, alternati tra loro. Il punto più alto è per la I ora, e via via gli altri per le ore successive, fino alla XI ora; manca il punto più basso per la XII e ultima ora: probabilmente non vi si faceva ricorso, poiché il finire della notte si poteva riconoscere semplicemente dallo svilupparsi del crepuscolo mattutino. Sopra l'apertura per il deflusso all'esterno v'era la figura di un babbuino, animale sacro a Thot, il dio lunare della misurazione del tempo; l'acqua defluiva forse attraverso il suo fallo e si presume che nell'apertura di deflusso si trovasse un sottile tubo di metallo. Poiché sinora tutti gli orologi ad acqua sono stati rinvenuti in frammenti e, inoltre, non è stato ancora scoperto nessuno di questi tubi, si è portati a credere che fossero fatti di un metallo nobile, con ogni probabilità oro. Mentre in passato gli orologi ad acqua dell'antico Egitto erano considerati uno strumento di misurazione del tempo piuttosto difettoso, le nuove ricerche hanno rivalutato la loro accuratezza.
Orologi solari
Orologi solari egizi sono conosciuti a partire dal Nuovo Regno (1540-1076), per quanto vi siano indicazioni sulla loro esistenza già mille anni prima. Questi orologi traggono l'informazione oraria dall'ombra di uno stilo (gnomone), verticale od orizzontale, illuminato dal Sole (donde l'altra loro denominazione di 'orologi a ombra') e, naturalmente, possono essere usati soltanto nelle ore diurne (sempreché il Sole non sia oscurato da nuvole, ma questa limitazione in pratica non valeva per l'Egitto); possono essere di due tipi, nel primo dei quali, quello maggiormente diffuso, si considera come indicazione oraria la lunghezza dell'ombra, mentre nel secondo come tale si considera la direzione dell'ombra.
Per il primo tipo, che è tuttora il più diffuso ed è detto 'orologio a lunghezza d'ombra', ci si serve di apposite tabelle, indicanti le lunghezze diverse dell'ombra dello gnomone alle diverse ore per ciascun mese; queste tabelle erano sui cosiddetti 'cubiti sacri', una sorta di regoli pentagonali lunghi un cubito (0,523 m ca.) che erano posizionati per questo scopo; tuttavia, a causa della mancanza di spazio, i cubiti sacri riportano soltanto indicazioni relative alle prime tre ore del giorno e alle ultime. Un orologio di questo tipo poteva, in linea di principio, essere abbastanza preciso, ma i testi contengono una serie di errori manifesti, per cui i riscontri hanno condotto a risultati piuttosto catastrofici. Poiché le discrepanze sono così grandi, non si può neanche escludere che l'interpretazione finora accettata, secondo cui le indicazioni di lunghezza nelle dette tabelle sono effettivamente lunghezze dell'ombra riferite a ore uguali, vada rivista.
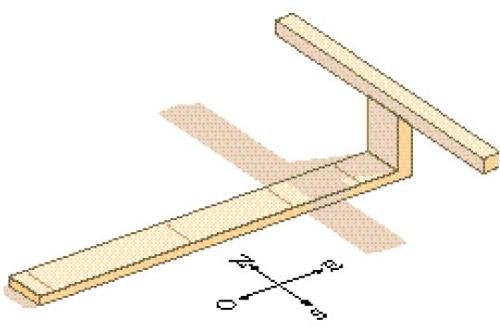
Una variante successiva consiste in un regolo di legno, lungo circa 30 cm, posto nella direzione est-ovest e a un capo del quale è inserito un regoletto rialzato perpendicolare, cioè nord-sud. Al centro della parte superiore del regolo sono incisi, a distanze crescenti dal rialzo, cinque piccoli cerchi accanto a ciascuno dei quali si trovano i nomi delle ore del giorno; i nomi della I e della XI ora stanno accanto al cerchio più distante dal rialzo, quelli della II e X ora vicino al cerchietto successivo verso il rialzo, e così via, mentre quello della VI ora, il mezzogiorno, si trova vicinissimo al rialzo. Esistono anche modelli provvisti soltanto di quattro segni, come nella figura; in questo caso si rinunciava alla misurazione della prima (e dell'ultima) ora a causa della lunghezza eccessiva dell'ombra. Per misurare le ore distanti dal mezzogiorno era sufficiente ruotare opportunamente il regolo. Poiché quest'ultimo è relativamente stretto, in molti periodi il limite dell'ombra gettata dal rialzo non avrebbe intercettato il regolo posto in direzione est-ovest, ma vi sarebbe caduto accanto, a nord o a sud; per questo motivo si presume che sul rialzo fosse posto di traverso un altro regolo (forse uno dei cubiti sacri) che gettava un'ombra lunga, da sud a nord, tale da intercettare in ogni caso il regolo con i segni di rilevamento. Il rapporto reciproco delle distanze dei singoli punti di misurazione è pari a numeri interi; l'orologio solare non garantiva pertanto una divisione del tempo regolare neppure agli equinozi. A ciò va aggiunto che una graduazione fissa sul regolo non può tenere conto della notevole differenza di lunghezza delle ombre a seconda della stagione.
Nel Museo del Cairo è conservato il modello di un orologio solare, risalente presumibilmente all'Età Tarda (712-332), che non ha soltanto un piano orizzontale d'intercettazione da entrambe le parti, ma contiene anche altri due orologi solari, uno con un piano d'intercettazione a forma di scala, l'altro con un piano d'intercettazione inclinato.
Il secondo tipo di orologio solare egizio è basato, com'è stato detto in apertura, sulla variazione non della lunghezza dell'ombra, ma della sua direzione. È costituito da una scala a forma di semicerchio, nella quale le singole ore sono indicate mediante incisioni distanti 15° l'una dall'altra; nel punto in cui le linee convergono si trova un foro, in cui è inserito uno stilo oppure un perno per sospendere l'orologio in direzione est-ovest. L'esemplare più antico risale al periodo di Merenptah (fine XIII sec.). Anche questi orologi fornivano un'indicazione delle ore piuttosto imprecisa.
Carte celesti
Una serie intera di carte celesti è conservata principalmente in tombe egizie e su sarcofagi. Fatta salva un'eccezione, esse sono però tanto schematiche da non avere pressoché alcun rilievo per la storia dell'astronomia. L'eccezione si trova presso Tebe, a Deir el-Bahari, nella tomba di Senenmut, visir e architetto della regina Hatshepsut all'inizio del Nuovo Regno (1473-1458 ca.). La tomba non è stata completata, e contiene ancora parte delle tracce preliminari che danno importanti indicazioni per interpretare la carta celeste.
La parte superiore di questa comprende le figure delle stelle del cielo meridionale; l'inferiore quelle del cielo settentrionale. I 12 cerchi rappresentano i mesi egizi, come mostrano i geroglifici sovrastanti; il primo mese si trova nell'angolo superiore destro, il dodicesimo nell'inferiore destro. Tra i mesi si distingue un lungo triangolo, il meridiano, sulla cui sommità si trova un piccolo cerchio collegato con la raffigurazione di un toro sul cui corpo sta il nome dell'Orsa Maggiore; poiché gli Egizi rappresentavano le sette stelle principali come un toro o, per lo più, come una coscia di toro, l'ultima stella, situata sul vertice del triangolo, va identificata con la stella η della detta costellazione (η Ursae Maioris). Se si prolungano la lancia del dio con testa di falco posto in basso e il meridiano, le due linee s'incontrano nel polo celeste (declinazione 90°); il meridiano stesso si trova sull'equatore celeste (declinazione 0°). La stella η Ursae Maioris è dunque disegnata nella sua collocazione esatta (declinazione 68,2°), come si può constatare attraverso misurazioni.
Si dice che una stella 'culmina' quando raggiunge il suo punto più alto (oppure più basso, nel caso delle stelle circumpolari) sul meridiano. Per gli Egizi assumeva grande importanza la culminazione a mezzanotte e da un calcolo a ritroso fatto per l'anno della carta stellare (il 1462 a.C., come si è visto in seguito) è risultato che la culminazione di mezzanotte di η Ursae Maioris ha avuto luogo nella notte tra il 18 e il 19 marzo. Ora, un esame ulteriore della carta mostra che i 12 mesi dell'anno egizio di 360 giorni sono suddivisi dal meridiano in tre parti uguali di 120 giorni. Se il 18/19 marzo fissa il limite tra la seconda e la terza sezione dell'anno, il nuovo passaggio dalla terza alla prima sezione deve avvenire 120 giorni più tardi, il 16/17 luglio. Questa data non è casuale, infatti proprio allora si verificava il cosiddetto 'sorgere eliaco' di Sirio che, come ricordato più volte, definiva il primo giorno dell'anno. Se dal 16/17 luglio si avanza di altri 120 giorni, si arriva al 14/15 novembre, limite tra la prima e la seconda sezione. Questa notte coincideva, a sua volta, con un evento astronomico significativo, la culminazione a mezzanotte della stella Rigel (β Orionis). Già in epoca molto antica Orione era equiparato dagli Egizi al dio Osiride. La sua stella principale, che è l'appena nominata Rigel (in arabo 'piede'), dava il nome all'intera costellazione: la parola egizia corrispondente significa tanto 'Orione' quanto 'dita dei piedi'. Anche quest'ultimo evento astronomico è rappresentato sul soffitto della tomba; il dio Orione si trova difatti in una barca nella parte superiore del dipinto, il cielo meridionale; una linea verticale, tracciata al centro, passerebbe esattamente attraverso le dita del suo piede sinistro, vale a dire attraverso Rigel.
Alla sinistra di Rigel è posta una donna in una barca, la dea Iside, equiparata nel cielo a Sirio. Ancora più a sinistra seguono due dèi con testa di falco (secondo le iscrizioni, i pianeti Giove e Saturno), che portano una stella sul capo e stanno anch'essi in una barca. Al margine estremo si trova il pianeta Venere, rappresentato dagli Egizi come un airone o una fenice. È raffigurato anche Mercurio, come una piccola figura di Seth a destra, sopra Venere; manca, invece, Marte, l'ultimo dei cinque pianeti noti nell'antichità. Si tratta di una lacuna rilevante in una carta celeste altrimenti così accurata, tanto più che nelle carte successive (tutte molto schematiche), Marte compare sempre in una barca dietro Giove e Saturno, come un terzo dio con testa di falco.
L'unica conclusione logica da trarre è che Marte, nella notte corrispondente alla raffigurazione, non fosse realmente visibile. Un'ulteriore circostanza permette di calcolare l'anno assoluto della rappresentazione, cioè che è ancora possibile notare i punti delle tracce relativi a Orione e a Giove; era evidentemente importante che la posizione fissata per i due corpi celesti fosse esatta. Sulla carta (nella quale tutti i luoghi di uguale longitudine presentano la stessa ascensione retta) la fascia occupata da Giove si trova tra 73° e 95° di ascensione retta. Poiché è approssimativamente noto quando visse Senenmut, si può risalire all'anno assoluto della carta. Nei 50 anni tra il 1505 e il 1455 c'è difatti soltanto un anno in cui Giove, nella notte tra il 14 e il 15 novembre, si trovava tra 73° e 95° di ascensione retta e, allo stesso tempo, Marte non era visibile. L'anno così ricavato (1463) si accorda d'altronde benissimo alle altre date della vita di Senenmut; il giorno cadeva nel XVII anno di regno di Thutmosi III. Il più recente degli óstraka ritrovati accanto all'ingresso della tomba, risale al XVI anno; a quell'epoca la tomba era di conseguenza ancora in costruzione. Poiché, d'altronde, la caduta di Senenmut avvenne nel XVIII o XIX anno, il XVII anno è del tutto plausibile per il soffitto astronomico. A sua volta, la datazione esatta della raffigurazione sul soffitto costituisce una fonte importante per la cronologia dell'inizio del Nuovo Regno.
Orientamento astronomico dei templi
L'orientamento astronomico delle costruzioni è un fenomeno proprio di molte culture antiche ma, almeno nel campo dell'egittologia, è tuttora poco studiato. Gli edifici più famosi con un orientamento astronomico sono le piramidi dell'Antico Regno, i cui lati si discostano dal vero nord solo di pochi minuti. Una serie intera di metodi consente di determinare la direzione sud-nord basandosi sull'osservazione delle stelle. Fra questi metodi fu molto probabilmente adottato quello che consisteva nell'osservare le due posizioni in cui una stella circumpolare attraversava un orizzonte artificiale e nell'unirle poi al sito di osservazione formando un triangolo isoscele dalla bisezione del quale risultava il meridiano sud-nord.
Oltre alle piramidi, probabilmente anche una serie di templi possedeva un orientamento astronomico, ma si è rivelato sinora difficile darne la prova. La ragione risiede semplicemente nell'inesattezza, in rapporto all'orientamento, di molte tra le piante pubblicate, anche in tempi recenti, poiché la maggior parte dei disegnatori non ha coscienza di questo problema. In molti casi la direzione nord è stata determinata con una bussola magnetica, senza indicare l'errore di misurazione, che è molto variabile; in aggiunta, le frecce per il nord sono generalmente così corte che soltanto per questo si devono calcolare da uno a due gradi di deviazione. Una ricerca geodetica che pubblicasse le misure ottenute insieme all'indicazione dell'altezza locale sull'orizzonte, fornirebbe qualche risultato supplementare. Devono inoltre essere fissati criteri chiari per stabilire che cosa possa essere considerato un orientamento astronomico e che cosa no. Soltanto se un determinato corpo celeste sta in relazione con la divinità principale del rispettivo tempio si potrà difatti presumere un orientamento realmente progettato; senza attenersi a questo criterio si potrà trovare una stella per ogni asse di tempio, abbandonando però il terreno della serietà scientifica. Casi di un orientamento astronomico sicuro possono essere finora considerati l'allineamento a nord del tempio di Edfu (con l'ausilio della culminazione inferiore di stelle dell'Orsa Maggiore, descritta anche nei testi); l'allineamento del tempio di Amon-Ra (dio Sole) sul solstizio d'inverno; quello sul sorgere di Sirio del piccolo tempio di Iside di Dendera e dell'asse trasversale del grande tempio di Hathor a Dendera.
Ancora del tutto inesplorata è la questione se gli architetti egizi abbiano tenuto conto nelle loro costruzioni della proiezione delle ombre in determinati periodi dell'anno e del giorno, e se in relazione a essa abbiano eventualmente collocato persino le decorazioni delle pareti e delle colonne dei templi.
La lunghezza della circonferenza terrestre
La maggior parte delle tombe dei re del Nuovo Regno, a partire da Thutmosi I (1504-1492), contengono l'Amduat, un libro che descrive il viaggio di 12 ore del dio Sole nell'aldilà notturno, dal tramonto a ovest fino all'alba a est. La II, la III e talora anche la I ora notturna indicano con precisione la misura del percorso compiuto in questo periodo: 309 iteru (egizio ı̓trw: 1 iteru equivale a 10,5 km ca.). Poiché le ore hanno uguale lunghezza temporale, si suppone che lo stesso valga per l'estensione spaziale e per il cammino percorso in ognuna di esse. L'indicazione di due o tre misure uguali costituisce un'informazione sufficiente; una ripetizione dalla IV ora fino alla XII sarebbe superflua. Le dette 309 iteru rappresentano presumibilmente un numero con un senso preciso poiché, quando gli Egizi volevano esprimere una grandezza enorme, sceglievano un numero tondo come, per esempio, mille iteru.
Il modo più semplice per capire quale ragionamento fosse implicito nell'indicazione è considerare l'intera lunghezza del mondo dell'aldilà egizio, moltiplicando 309 iteru per 12: ne risultano 309×12×10,5=38.934 km ca. Questi 39.000 km scarsi ricordano la lunghezza della circonferenza terrestre all'equatore (40.075 km), distanza che, se si presuppone una forma sferica della Terra, corrisponde sostanzialmente al corso apparente del Sole sul 'cielo notturno' dal tramonto, a ovest, fino all'alba, a est.
Per verificare quale sia la lunghezza della circonferenza terrestre in base al calcolo forse più semplice (effettuato in quanto una distanza nota nord-sud corrisponde alla differenza dell'angolo di incidenza dei raggi solari) si deve partire dalla curvatura terrestre in Egitto. A una latitudine geografica media di 27° si ottiene come risultato una circonferenza terrestre di 3814 iteru, cioè 40.047 km ca.; poiché il Sole durante il percorso notturno compie 3708 iteru, ne avanzano ancora 106 per il percorso diurno. Se si suppone che gli Egizi avessero avuto idea della forma sferica della Terra, allora si sarebbero trovati di fronte al problema di dividere la circonferenza terrestre tra percorso diurno e percorso notturno; da tali calcoli avrebbero dovuto comprendere chiaramente che la distanza percorsa di giorno (potevano ancora controllare) doveva essere notevolmente più piccola del percorso notturno. L'esatta determinazione del percorso dall'orizzonte est a quello ovest avrebbe potuto tuttavia procurare delle difficoltà alle quali rimediarono, probabilmente, immaginando l'orizzonte come un cerchio e fissandone come diametro l'intera lunghezza dell'Egitto, che ammontava canonicamente a 106 iteru; sottraendo questa lunghezza dall'intera lunghezza di 3814 iteru e dividendo il resto per 12 si ottiene 309 iteru come lunghezza di un'ora notturna.
Se le riflessioni precedenti sono corrette, gli Egizi avrebbero dunque calcolato la lunghezza della circonferenza terrestre, in modo sorprendentemente accurato, oltre mille anni prima di Eratostene (il quale usò peraltro un ineccepibile metodo astronomico-geometrico).
Bibliografia
Beckerath 1993: Beckerath, Jürgen von, Bemerkungen zum ägyptischen Kalender, "Zeitschrift für ägyptische Sprache und Altertumskunde", 120, 1993, pp. 7-22; pp. 131-136.
Borchardt 1920: Borchardt, Ludwig, Die altägyptische Zeitmessung, in: Die Geschichte der Zeitmessung und der Uhren, hrsg. von Ernst von Bassermann-Jordan, Berlin-Leipzig, Vereinigung wissenschaftlicher Verleger, 1920-1925; v. I., fasc. B: Wasser- und Sonnenuhren, 1920.
Depuydt 1996: Depuydt, Leo, The function of the Ebers Calendar concordance, "Orientalia", 65, 1996, pp. 61-88.
Fermor 1983: Fermor, John H. - Burgess, Arthur E. - Przybylinski, Victor, The timekeeping of Egyptian outflow clocks, "Endeavour", n. s., 7, 3, 1983, pp. 133-136.
Ferrari d'Occhieppo 1996: Ferrari d'Occhieppo, Konradin - Kraus, Rolf - Schmidt-Kaler, Theodor, Die Gefilde der altägyptischen Unterwelt: Spiegelbild der Sonnenbahnen im Jahreslauf, "Zeitschrift für ägyptische Sprache und Altertumskunde", 123, 1996, pp. 103-110.
Ingham 1969: Ingham, M.F., The length of the Sothic cycle, "Journal of Egyptian Archaeology", 55, 1969, pp. 36-40.
Krauss 1985: Krauss, Rolf, Sothis- und Monddaten. Studien zur astronom. und technischen Chronologie Altägyptens, Hildesheim, Gerstenberg, 1985.
‒ 1995: Krauss, Rolf, Nochmals die ägyptische Nacht vom 14./15. November 1463 v. Chr., "Göttinger Miszellen", 146, 1995, pp. 61-70.
Lange 1940: Papyrus Carlsberg No. I. Ein hieratisch-demotischer kosmologischer Text, hrsg. und bearb. von Hans Ostenfeld Lange, Otto Neugebauer, København, E. Munksgaard, 1940.
Leitz 1991: Leitz, Christian, Studien zur ägyptischen Astronomie, 2. ed., Wiesbaden, O. Harrassowitz, 1991 (1. ed.: 1989).
‒ 1993: Leitz, Christian, Die Nacht des Kindes in seinem Nest in Dendara, "Zeitschrift für ägyptische Sprache und Altertumskunde", 120, 1993, pp. 136-165, p. 181.
‒ 1994a: Leitz, Christian, Der Mondkalender und der Beginn des ägyptischen Kalendertages, "Bulletin de la Société d'Égyptologie", 18, 1994, pp. 49-60.
‒ 1994b: Leitz, Christian, Tagewählerei Das Buch ḥ3t nḥḥ pḥ.wy ḏt und verwandte Texte, Wiesbaden, O. Harrassowitz, 1994.
‒ 1995: Leitz, Christian, Altägyptische Sternuhren, mit einem Beitrag von Heinz-J. Thissen, Leuven, Uitgeverij Peeters en Departement Orientalistiek, 1995.
Luft 1992: Luft, Ulrich, Die chronologische Fixierung des ägyptischen Mittleren Reiches nach dem Tempelarchiv von Illahun, Wien, Verlag der Österreichischen Akademie der Wissenschaften, 1992.
Mackensen 1978: Mackensen, Ludolf von, Neuere Ergebnisse zur ägyptischen Zeitmessung: die Inbetriebnahme und Berechnung der ältesten erhaltenen Wasseruhr, München, Callwey, 1978.
Neugebauer 1942: Neugebauer, Otto, Egyptian planetary texts, "Transactions of the American Philosophical Society", 32, 2, 1942, pp. 209-250.
‒ 1960: Neugebauer, Otto - Parker, Richard A., Egyptian astronomical texts, Providence (R.I.), published for Brown University Press, by L. Humphries, 1960-1969, 3 v.; v. I: The early decans, 1960.
‒ 1964: Neugebauer, Otto - Parker, Richard A., Egyptian astronomical texts, Providence (R.I.), published for Brown University Press, by L. Humphries, 1960-1969, 3 v.; v. II: The Ramesside star clocks, 1964.
‒ 1969: Neugebauer, Otto - Parker, Richard A., Egyptian astronomical texts, Providence (R.I.), published for Brown University Press, by L. Humphries, 1960-1969, 3 v.; v. III, 1-3: Decans, planets, constellations and zodiacs, 1969.
Parker 1950: Parker, Richard Anthony, The calendars of ancient Egypt, Chicago, University of Chicago Press, 1950.
‒ 1959: Parker, Richard A., A Vienna demotic papyrus on eclipse and lunar-omina, Providence, Brown University Press, 1959.
Pécoil 1986: Pécoil, Jean François, Le soleil et la cour d'Edfou, "Bulletin de l'Institut français d'archéologie orientale", 86, 1986, pp. 277-301.
Ramsès le Grand, exposition, Galeries nationales du Grand Palais, [Paris, 11 mai - 15 octobre], catalogue sous la direction de Christiane Desroches Noblecourt, Paris, Association française d'action artistique, 1976, pp. 139-149, tav. 33.
van der Waerden 1980: van der Waerden, Bartel L., Erwachende Wissenschaft, 2. ed., Basel, Birkhäuser, 1966-1980, 2 v.; v. II: Die Anfänge der Astronomie, 1980 (1. ed.: 1956-1968).
Zába 1953: Zába, Zbynèk, L'orientation astronomique dans l'ancienne Égypte, et la précession de l'axe du monde, Prague, Éd. de l'Académie tchécoslovaque des sciences, 1953.
Zeidler 1997: Zeidler, Jürgen, Die Länge der Unterwelt nach ägyptischer Vorstellung, "Göttinger Miszellen", 156, 1997, pp. 100-112.