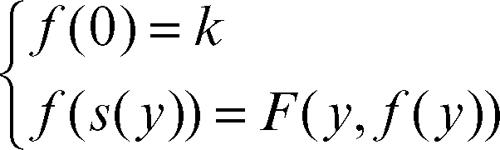ricorsione
ricorsione
ricorsione in logica, uno dei tre schemi per la costruzione di una → funzione ricorsiva a partire dalle funzioni base (annullatore, successore e proiettori), insieme allo schema della composizione e allo schema della minimalizzazione. Una funzione ƒ di n + 1 variabili ƒ(x1, ..., xn, y) è definita (o costruita) per ricorsione a partire da una funzione di n argomenti h(x1, ..., xn) e da una funzione di n + 2 argomenti F(x1, ..., xn, z, y) secondo il seguente procedimento:
dove s(y) indica il successore di y. La F permette così di calcolare il valore della funzione ƒ in corrispondenza di un certo valore della variabile y a partire dal valore che essa assume in corrispondenza del valore precedente di y. È possibile completare la definizione nel caso n = 0 a partire da un numero naturale assegnato k e una funzione ricorsiva F di due argomenti nel modo seguente:
In informatica, il termine ricorsione è conseguentemente utilizzato per indicare il processo di applicazione di una → regola ricorsiva, secondo uno schema di calcolo per il quale il valore di una funzione a un dato passo n, indicato con ƒ(n), è calcolato attraverso il valore della stessa funzione al passo n − 1, cioè ƒ(n − 1), che a sua volta è calcolato per mezzo di ƒ(n − 2) fino ad arrivare al valore di base ƒ(0). Questo schema di calcolo è largamente utilizzato nella programmazione attraverso la definizione di procedure che richiamano sé stesse e che sono appunto dette procedure ricorsive.