Hilbert, David
Enciclopedia on line
 {{{1}}}
Matematico tedesco (Königsberg 1862 - Gottinga 1943). È la figura più notevole della matematica della prima metà del Novecento e forse dell'intero secolo. A Königsberg frequentò l'università con [...] notevole mole di lavoro tecnico in questa direzione, i risultati di K. Gödel dimostrarono sostanzialmente l'impossibilità del sogno hilbertiano. Forse H. non ne fu mai convinto ma una delle sue ultime opere, i monumentali Grundlagen der Mathematik ...
Leggi Tutto
{{{1}}}
Matematico tedesco (Königsberg 1862 - Gottinga 1943). È la figura più notevole della matematica della prima metà del Novecento e forse dell'intero secolo. A Königsberg frequentò l'università con [...] notevole mole di lavoro tecnico in questa direzione, i risultati di K. Gödel dimostrarono sostanzialmente l'impossibilità del sogno hilbertiano. Forse H. non ne fu mai convinto ma una delle sue ultime opere, i monumentali Grundlagen der Mathematik ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
spazio di Hilbert
Enciclopedia della Scienza e della Tecnica (2008)
spazio di Hilbert
Arrigo Cellina
Per poter enunciare il teorema di Pitagora nel piano, occorre definire quando due vettori sono tra loro ortogonali; ciò si ottiene dalla nozione di prodotto scalare [...] , che associa a due vettori un numero reale (questo numero è zero se i due vettori sono ortogonali). Uno spazio di Hilbert ℋ è uno spazio di Banach che generalizza il normale piano euclideo, ossia su cui è definito un prodotto scalare. Si tratta ...
Leggi Tutto
CATEGORIA:
ANALISI MATEMATICA
hilbertiano
Dizionario delle Scienze Fisiche (1996)
hilbertiano
hilbertiano [agg. Der. del cognome di D. Hilbert] [ALG] [ANM] Qualifica di enti e nozioni introdotti da D. Hilbert, equivalente a "di Hilbert": spazio h. o spazio di Hilbert, ecc. ...
Leggi Tutto
Haar, Alfred
Enciclopedia on line
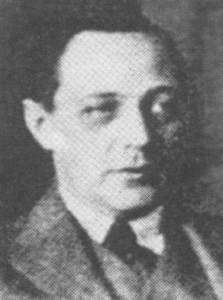 Matematico ungherese (Budapest 1885 - Szeged 1933), allievo di D. Hilbert, prof. di fisica-matematica a Kolozsvár (1912) e quindi (dal 1920) di matematica a Szeged. I suoi contributi scientifici vanno [...] a J. L. von Neumann e a L. S. Pontrjagin la soluzione, per i gruppi compatti, del celebre "5º problema di Hilbert" che consisteva nel caratterizzare i gruppi di Lie mediante proprietà topologiche. Insieme con F. Riesz fondò (1922) la rivista Acta ...
Leggi Tutto
Matematico ungherese (Budapest 1885 - Szeged 1933), allievo di D. Hilbert, prof. di fisica-matematica a Kolozsvár (1912) e quindi (dal 1920) di matematica a Szeged. I suoi contributi scientifici vanno [...] a J. L. von Neumann e a L. S. Pontrjagin la soluzione, per i gruppi compatti, del celebre "5º problema di Hilbert" che consisteva nel caratterizzare i gruppi di Lie mediante proprietà topologiche. Insieme con F. Riesz fondò (1922) la rivista Acta ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
operatori compatti
Enciclopedia della Scienza e della Tecnica (2008)
operatori compatti
Luca Tomassini
Operatori lineari su uno spazio di Hilbert ℋ vicini in un senso opportuno agli operatori di dimensione finita, ovvero agli operatori che mandano ℋ in un sottospazio [...] x,x)≤1) è chiusa e limitata ma non compat ta. Segue immediatamente che l’operatore identità su uno spazio di Hilbert di dimensione infinita non è compatto, mentre lo sono per definizione gli operatori di dimensione finita. Questi ultimi permettono di ...
Leggi Tutto
CATEGORIA:
ANALISI MATEMATICA
metamatematica
Enciclopedia on line
Scienza che ha per oggetto l’analisi formale delle strutture matematiche, e che si può identificare con la logica matematica. Con significato più ristretto la m., o teoria della dimostrazione (Beweistheorie), [...] intorno al 1919, avente per oggetto intere teorie matematiche e le relative proprietà strutturali. Per l’indirizzo ideato da Hilbert (➔ formalismo), il fine ultimo della m. è di chiarire i fondamenti della matematica, in modo da metterla al riparo ...
Leggi Tutto
CATEGORIA:
LOGICA MATEMATICA
Courant, Richard
Enciclopedia on line
 Matematico prussiano (Lublinitz, Prussia, 1888 - New Rochelle 1972). Allievo di D. Hilbert all'univ. di Gottinga, prof. a Münster e Gottinga dal 1920 al 1934, emigrò poi negli USA in seguito all'avvento [...] formale. Sono ormai classici i suoi numerosi trattati e saggi (alcuni dei quali scritti in collaborazione con altri illustri studiosi, come Hilbert, von Mises, Cohn-Vossen, ecc.); tra questi: Methoden der mathematischen Physik (in collab. con D ...
Leggi Tutto
Matematico prussiano (Lublinitz, Prussia, 1888 - New Rochelle 1972). Allievo di D. Hilbert all'univ. di Gottinga, prof. a Münster e Gottinga dal 1920 al 1934, emigrò poi negli USA in seguito all'avvento [...] formale. Sono ormai classici i suoi numerosi trattati e saggi (alcuni dei quali scritti in collaborazione con altri illustri studiosi, come Hilbert, von Mises, Cohn-Vossen, ecc.); tra questi: Methoden der mathematischen Physik (in collab. con D ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
Ritz, Walter
Enciclopedia on line
Fisico e matematico svizzero (Sion 1878 - Gottinga 1909), allievo di D. Hilbert, W. Voigt e H. A. Lorentz. Compì numerose ricerche di spettroscopia, enunciando il principio di combinazione che porta il [...] suo nome. Sviluppò un nuovo metodo di calcolo per i problemi dipendenti da equazioni a derivate parziali. Concepì una nuova elettrodinamica, rimasta peraltro soltanto allo stato di abbozzo per la sua morte ...
Leggi Tutto
Dehn, Max
Enciclopedia on line
Matematico tedesco (Amburgo 1878 - Black Mountain, North Carolina, 1952). Allievo di D. Hilbert a Gottinga, professore alle università di Breslavia (1913) e di Francoforte sul Meno (1921), nel 1935 fu [...] costretto a emigrare per motivi razziali. Gli studî del D. vanno dai fondamenti della geometria (geometria non archimedea) alla topologia (teoria dei nodi). A lui è dovuta, in particolare, la seguente ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
autoaggiunto
Dizionario delle Scienze Fisiche (1996)
autoaggiunto
autoaggiunto [agg. Comp. di auto- e aggiunto] [ANM] Di operatore lineare che è identico al suo operatore aggiunto (anche come s.m.); il termine è sinon. di hermitiano (←) per operatori definiti [...] su spazi finito-dimensionali, mentre non lo è se lo spazio è infinito-dimensionale; precis., dato uno spazio di Hilbert H, l'a. è un operatore lineare A per cui è (a, Ab)=(Aa, b) con a∈H, b∈H. ◆ [ALG] Elemento a., o hermitiano, di un'algebra di ...
Leggi Tutto