Bravais, reticolo di
Bravais, reticolo di
Bravais, reticolo di in geometria e in cristallografia, insieme infinito di punti dello spazio, generati mediante traslazioni. Assumendo come origine del riferimento cartesiano uno qualsiasi dei punti del reticolo, ogni altro punto è individuato da un vettore della forma: v = ia1 + ja2 + ka3 dove i, j, k sono numeri interi; a1, a2, a3 sono detti i vettori generatori del reticolo. Un reticolo di Bravais si può suddividere in un numero infinito di celle di forma poliedrica tutte uguali, che riempiono lo spazio. Si considerano diversi tipi di celle:
• la cella primitiva, che è il poliedro i cui vertici sono otto punti del reticolo tra loro contigui:
v1 = ia1 + ja2 + ka3
v2 = (i + 1)a1 + ja2 + ka3
v3 = ia1 + (j + 1)a2 + ka3
v4 = (i + 1)a1 + (j + 1)a2 + ka3
v5 = ia1 + ja2 + (k + 1)a3
v6 = (i + 1)a1 + ja2 + (k + 1)a3
v7 = ia1 + (j + 1)a2 + (k + 1)a3
v8 = (i + 1)a1 + (j + 1)a2 + (k + 1)a3
• la cella convenzionale, che è la cella del sistema cristallino corrispondente al reticolo;
• la cella di Wigner-Seitz, che è il luogo geometrico dei punti dello spazio la cui distanza da un punto fissato del reticolo è minore o uguale di quelle da tutti gli altri punti del reticolo.
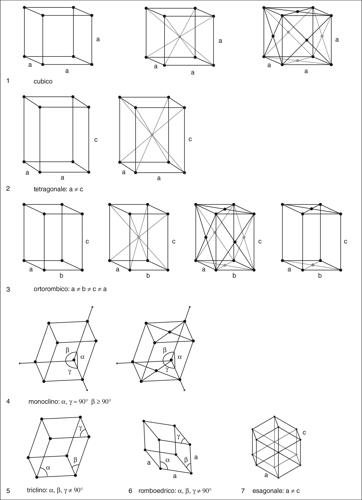
I reticoli di Bravais si classificano in base alla forma della cella convenzionale (ciascuna forma corrisponde a uno dei sette sistemi cristallini) e alla presenza o meno di punti del reticolo al centro del corpo o delle facce di questa. Esistono 14 tipi di reticoli di Bravais.