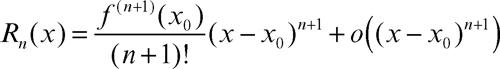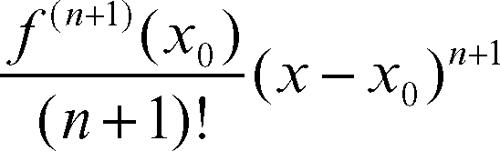Peano, resto di
Peano, resto di
Peano, resto di espressione del resto per la formula di → Taylor utile per lo studio locale delle linee. Se una funzione f(x), reale di variabile reale, è continua con tutte le sue derivate fino all’ordine n-esimo in un intorno del punto x0 ed è dotata della derivata (n + 1)-esima nel punto x0, si può scrivere il resto nella forma
dove il simbolo o indica → o piccolo. Questa forma del resto è importante perché, se questa derivata è diversa da zero, per il teorema della permanenza del segno il resto assume un segno ben definito in un opportuno intorno di x0, consentendo di determinare il comportamento relativo dei grafici della funzione e del polinomio di Taylor. Precisamente, se n è dispari, e quindi n + 1 pari, il fattore (x − x0)n+1 è positivo per x ≠ x0, e quindi Rn(x) ha il segno di ƒ (n+1)(x0) e il grafico di f(x) non attraversa quello del polinomio. Invece, se n è pari il fattore (x − x0)n+1 cambia segno a seconda che x sia maggiore o minore di x0, e pertanto i due grafici si attraversano.
Naturalmente il termine
potrebbe essere aggiunto al polinomio di Taylor aumentandone il grado; in tal caso però l’informazione residua è solo che l’errore è
informazione utile per una valutazione asintotica e quindi per il calcolo di limiti.
Il resto di Peano si generalizza inoltre a funzioni di più variabili, sostituendo a
il termine
