rendita
rendita
rendita in matematica finanziaria, successione di capitali da versare o da riscuotere a scadenze prefissate. Ciascuno dei capitali che costituiscono una rendita è detta rata. Le rate possono essere tutte di uguale importo o di importi diversi e possono inoltre essere pagate o riscosse a cadenze regolari o irregolari. Le rate possono essere versate per estinguere un debito (→ ammortamento) oppure per costituire un capitale (→ capitale, costituzione di un).
In base al principio di → equivalenza finanziaria i capitali che costituiscono una rendita possono essere tutti valutati in un medesimo istante, per esempio al tempo t = 0, rispetto al quale si calcola il → valore attuale dei capitali che costituiscono la rendita, o anche al tempo in cui si effettua l’ultimo versamento o nell’unità di tempo immediatamente successiva, rispetto al quale viene invece calcolato il → montante di tutte le rate.
Le rate che costituiscono una rendita possono essere tutte di uguale importo, e la rendita è allora detta a rate costanti, oppure di importi diversi, e la rendita è allora detta a rate non costanti. Per il primo tipo di rendita si possono costruire formule di sintesi, per esempio per il calcolo del valore attuale. Per il secondo tipo di rendite, invece, non si possono in generale individuare formule di sintesi e il valore attuale A di una rendita è la somma dei valori attuali delle singole rate Ri, versate al tempo ti, che la costituiscono:
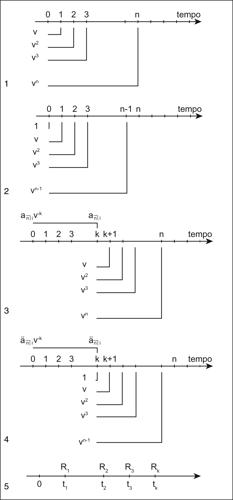
Le rate di una rendita possono inoltre essere anticipate o posticipate, a seconda che il versamento avvenga all’inizio o alla fine di ogni periodo unitario di tempo e la prima rata può essere immediata, cioè esigibile o versata al tempo t = 0 o al tempo t = 1, oppure differita, cioè esigibile o versata successivamente. Una rendita può infine essere costituita da un numero finito o infinito di rate e si ha rispettivamente una rendita temporanea o una rendita illimitata o perpetua o vitalizia (→ assicurazione). Data una rendita immediata, posticipata e temporanea n, cioè costituita da n rate, con rata costante unitaria, il suo valore complessivo al tempo t = 0, cioè il suo valore attuale, si ottiene calcolando la somma di una progressione geometrica di n termini di ragione il fattore di sconto v = (1 + i)−1 e primo termine v. Nella tradizione della matematica finanziaria il valore attuale di una rendita di questo tipo, valutata al tasso di interesse i, si indica con
che si legge «a figurato n, posticipato al tasso i». Si ha:
Per una rendita di rata R, il valore attuale è proporzionale al valore di
e si ha:
Il valore attuale di una rendita immediata, anticipata e temporanea n, cioè con n rate unitarie, è la somma di una progressione geometrica di n termini, ragione v e primo termine 1. Il suo valore attuale, tradizionalmente indicato con
che si legge «a anticipato, figurato n al tasso i», è:
Se la rendita è di rata R, allora il suo valore attuale, A anticipato, è:
Il valore attuale di una rendita differita, posticipata e temporanea n, a rate unitarie, si ottiene calcolandone il valore attuale al tempo t = k e scontando tale valore per k periodi di tempo. Si ha:
Analogamente al caso delle rendite immediate, il valore attuale di una rendita differita, anticipata e temporanea n si ottiene moltiplicando per il fattore 1/v il valore attuale al tempo t = k ed è:
Il valore attuale di una rendita illimitata, posticipata e immediata, cioè potenzialmente costituita da infinite rate (è questo il caso delle rendite fondiarie o, approssimativamente, delle concessioni demaniali a lunghissimo termine), si ottiene calcolando il limite (supponendo la rata unitaria):
Se la rendita è costituita da rate derivanti da un contratto di assicurazione, la rendita si chiama attuariale e, subentrando un fattore casuale, è trattata come una assicurazione.