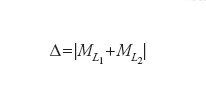regola di Wigner
regola di Wigner
In fisica quantistica, regola che governa le transizioni di molecole tra stati elettronici, in base alla quale risultano permesse solo le transizioni tra stati aventi la stessa molteplicità di spin, mentre sono proibite quelle fra stati cui corrisponde diversa molteplicità di spin. La molteplicità di spin è il numero di stati degeneri, cui corrisponde cioè lo stesso valore dell’energia, di sistemi quantistici in cui sono presenti particelle aventi un momento angolare intrinseco di spin. Nel caso in cui siano presenti più particelle identiche la degenerazione dipende dal numero quantico di spin totale S del sistema, ottenuto sommando i valori corrispondenti alle singole particelle, nel caso degli elettroni pari a 1/2. Riferendoci agli atomi, le regole che ne caratterizzano la molteplicità si ricavano definendo il valore del momento angolare totale, somma dei momenti angolari orbitali L e di spin S corrispondenti alla somma di quelli dei diversi elettroni. Si assume allora che, in accordo alla regola di Russel-Saunders, L e S si combinino per dare un momento angolare totale J, i cui possibili valori determinano la molteplicità dello stato e quindi le caratteristiche del corrispondente termine spettrale. I possibili valori di J sono
L+S, L+(S−1), L+(S−2), …, |L−S|
ovvero presentano 2S+1 possibili valori che nell’insieme definiscono la molteplicità di spin. Le regole precedenti si applicano anche alle molecole; in questo caso, se ML1 e ML2 sono i numeri quantici magnetici corrispondenti a momenti angolari L1 ed L2 degli atomi separati, il momento angolare della molecola vale
mentre il suo spin totale si valuta con la relazione seguente:
S=S1+S2
dove i due termini S1 e S2 si riferiscono agli atomi separati.