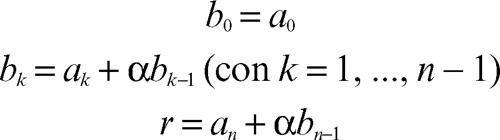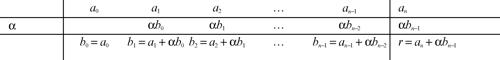Ruffini, regola di

Ruffini, regola di

Ruffini, regola di nel calcolo letterale, procedimento per la determinazione del quoziente

e del resto r della divisione di un polinomio a(x) = a₀xⁿ + ... + a_n di grado n ≥ 1 per un binomio di primo grado della forma x − α: i coefficienti b_i e il numero r sono dati ricorsivamente dalle formule

Il procedimento è riassunto schematicamente nel modo seguente. Si scrivono i coefficienti del polinomio a(x) e il termine noto del divisore in tabella come segue

A partire da tale tabella, possono essere calcolati iterativamente i coefficienti del polinomio quoziente q(x) e il resto r nel modo seguente. Si pone b₀ = a₀ e si scrive tale valore nella tabella in basso a sinistra; si calcola allora il prodotto αb₀ e lo si scrive nella tabella sotto a₁; si calcola infine la somma in colonna a₁ + αb₀ e si pone b₁ uguale a tale risultato. Si ripete il procedimento, sostituendo a₂ ad a₁ e b₁ a b₀, e ponendo b₂ = a₂ + αb₁. Iterando il procedimento descritto e ponendo r al posto di b_n nell’ultima iterazione, si riempie lo schema nel modo seguente

Nello schema risultano ora espressi i coefficienti del quoziente e il resto:

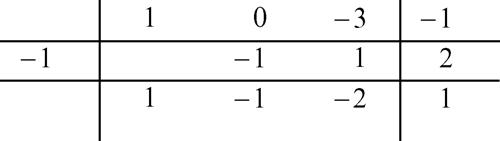
Per esempio, se a(x) = x ³ − 3x − 1 e α = −1, allora lo schema finale che si ottiene è

da cui si ricavano il quoziente q(x) = x ² − x − 2 e il resto r = 1.