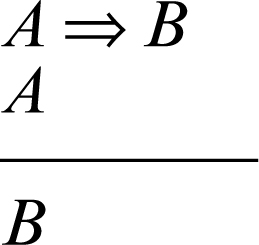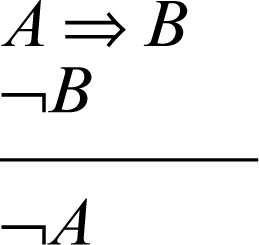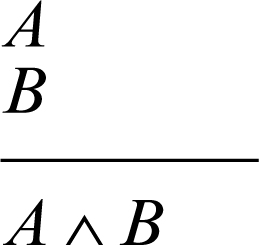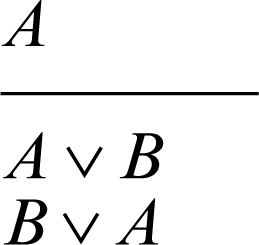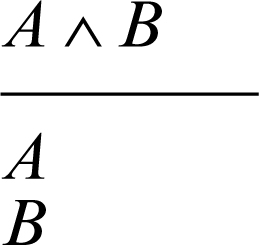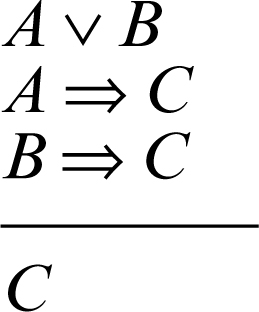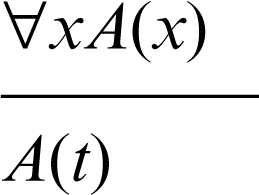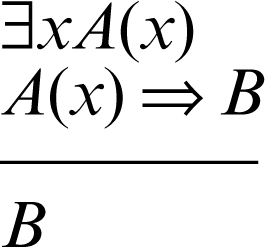inferenza, regola di

inferenza, regola di

inferenza, regola di locuzione equivalente a regola di deduzione o regola di derivazione logica (→ deduzione, regola di); essa designa una regola che permette di passare da una affermazione a un’altra in una catena di deduzione logica (→ deduzione, catena di). Così procedendo, si deduce (cioè si dimostra) un teorema a partire da assiomi (proposizioni inizialmente assunte come vere). Esempi di regole di inferenza sono (la linea orizzontale indica l’inferenza):

• modus ponens:

• modus tollens:

• introduzione della congiunzione (da A vera e B vera si deduce la verità di A ∧ B):

• introduzione della disgiunzione (da A vera si deduce la verità sia di A ∨ B sia di B ∨ A):

• eliminazione della congiunzione (da A ∧ B vera si deduce la verità sia di A sia di B):

• eliminazione della disgiunzione (da A ∨ B vera e da A ⇒C e B ⇒C vere, si deduce la verità di C):

Regole di inferenza di introduzione o eliminazione di quantificatori sono presenti anche nel linguaggio

dei predicati:

• eliminazione del quantificatore universale (se è vera ∀xA(x) allora sono vere le forme A(t ) per ogni t; è detta anche regola di particolarizzazione):

• eliminazione del quantificatore esistenziale (se è vera ∃xA(x) e si dimostra B da A(x), allora senza alcuna ipotesi su x si deduce B):

• introduzione del quantificatore universale (se è vera A(x) senza alcuna ipotesi su x, allora si deduce la verità di ∀xA(x); è detta anche regola di generalizzazione);

• introduzione del quantificatore esistenziale (se è vera A(t ), allora si deduce la verità di ∃xA(x); è detta anche regola di esistenzializzazione).