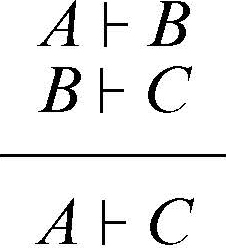deduzione, regola di
deduzione, regola di
deduzione, regola di locuzione equivalente a regola di → inferenza; indica una regola che permette il passaggio da una formula ben formata (ƒbƒ) a un’altra in una catena di deduzione. In un calcolo logico (calcolo degli enunciati, calcolo dei predicati, calcolo dei sequenti) i ragionamenti sono rappresentati formalmente attraverso catene di deduzione. Un ragionamento è infatti una successione di conseguenze logiche che portano da un’affermazione all’altra. La sua rappresentazione formale è, quindi, una successione finita di formule ben formate collegate l’una all’altra tramite regole che sono appunto dette regole di deduzione o regole di inferenza. Nella catena di deduzione le formule ben formate da cui si parte (che possono anche ridursi a una) sono gli assiomi del sistema formale preso in considerazione, mentre la ƒbƒ a cui si arriva è il teorema. Il → modus ponens (mp), il → modus tollens (mt) o l’introduzione della congiunzione (ic), che permette di dedurre da due formule (A, B) la loro congiunzione, cioè la formula A ∧ B, sono regole di deduzione presenti nel calcolo degli enunciati e nel calcolo dei predicati. Nel calcolo dei predicati un esempio di regola di deduzione è la particolarizzazione, che permette di dedurre da una formula in cui una variabile compare legata da un quantificatore universale (∀x, A(x), che si legge «per ogni x, A di x») una proposizione particolare ottenuta sostituendo alla variabile una costante del linguaggio formale (A(k) dove k è la costante).
Nel calcolo dei sequenti, invece, le regole di deduzione si dividono in regole logiche (per la congiunzione, la disgiunzione, la negazione, l’implicazione, la quantificazione universale e la quantificazione esistenziale), regole strutturali (indebolimento, scambio e contrazione) e regola del taglio. Quest’ultima può essere enunciata come segue: se da una premessa A è possibile dedurre una conseguenza B (in simboli, A ⊢ B) e se da B è possibile dedurre C (in simboli, B ⊢ C) allora dalla premessa A è possibile dedurre direttamente la formula C (in simboli, A ⊢ C):
Questa regola esprime formalmente l’uso dei lemmi in una deduzione, cioè la prassi di dimostrare un’affermazione facendo uso di teoremi precedentemente dimostrati. Vale tuttavia l’importante teorema di eliminazione del taglio (Hauptsatz) dimostrato da G. Gentzen nel 1934 (→ taglio, regola del). Per ulteriori esempi si veda → inferenza, regola di.