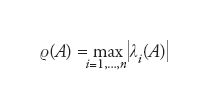raggio spettrale

raggio spettrale

Si consideri una matrice quadrata A∈ℂ^n×n e siano λ_i(A)∈ℂ i suoi autovalori. Ricordiamo che λ è un autovalore di A se esiste un vettore non nullo x∈ℂⁿ tale che Ax=λx; x è a sua volta detto autovettore associato a λ. Si definisce raggio spettrale di A il numero reale positivo

Esso rappresenta il raggio della più piccola circonferenza del piano complesso centrata nell’origine al cui interno giace lo spettro (ossia l’insieme degli autovalori) della matrice A. L’analisi del raggio spettrale di una matrice entra in gioco nello studio della convergenza dei metodi iterativi per la risoluzione di sistemi lineari. Infatti, dato un sistema lineare quadrato Ax=b, x,b∈ℂⁿ un metodo iterativo per la sua risoluzione può essere formulato come x^(k+1)=Bx^(k)+g, per k≥1 con x⁽⁰⁾ dato, a patto che la matrice di iterazione B e il vettore g∈ℂⁿ soddisfino la relazione di consistenza g=(I−B)A⁻¹b. Si può dimostrare che la successione x^(k) converge alla soluzione x del sistema lineare Ax=b, per ogni scelta del dato iniziale x⁽⁰⁾, se e solo se ϱ(B)〈1. In particolare un metodo iterativo converge tanto più velocemente quanto più ϱ(B) è prossimo a zero. Per misurare quanto un metodo iterativo converge velocemente alla soluzione del sistema lineare si può utilizzare la quantità R(B)=−log ϱ(B), detta velocità di convergenza.

→ Computazionali, metodi