QUASI-CRISTALLI
Quasi-cristalli
(App. V, iv, p. 376)
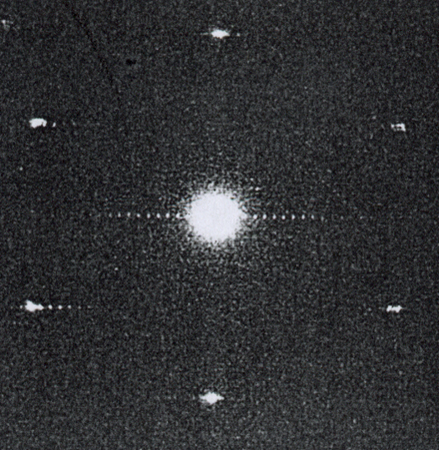
Mentre la simmetria pentagonale è frequente nel mondo organico, non la si riscontra fra le più perfette creazioni della natura inorganica, i cristalli. La struttura periodica del reticolo cristallino impedisce la presenza di assi di simmetria rotazionale di ordine diverso da 2, 3, 4 e 6, corrispondenti rispettivamente a rotazioni di 180°, 120°, 90° e 60°. I diagrammi di Laue ottenuti per diffrazione di raggi X o elettroni da un cristallo consistono di ben definite macchiette luminose, la cui disposizione simmetrica riflette la simmetria del cristallo. Al contrario, i diagrammi di Laue di un solido policristallino, un liquido o un solido amorfo sono costituiti da anelli diffusi. La simmetria traslazionale dei cristalli era pertanto ritenuta una condizione necessaria per ottenere diagrammi di Laue consistenti di punti luminosi ben definiti. Non a caso, perciò, ha destato grande interesse, presso la comunità scientifica internazionale, la scoperta fatta nel 1982 da D. Shechtman che i diagrammi di Laue, ottenuti per diffrazione di raggi X, del composto intermetallico Al₈₀Mn₂₀ erano costituiti da punti luminosi come quelli dei cristalli ma presentavano la simmetria pentagonale dell'icosaedro, incompatibile con l'invarianza traslazionale della struttura atomica. Così era stato trovato un nuovo tipo di struttura atomica dei solidi che, a causa della definizione del diagramma di diffrazione, deve presentare un ordine a lungo raggio nelle posizioni degli atomi, diverso però, per la presenza della simmetria pentagonale, dal tradizionale ordine periodico del reticolo cristallino. I materiali con questo tipo di struttura sono stati chiamati quasi-cristalli.
A tutt'oggi sono state sintetizzate parecchie centinaia di materiali quasicristallini, la maggior parte contenenti Al, come Al₆₅Cu₂₀Fe₁₅, Al₇₀Pd₂₀Mn₁₀, ma anche Ga₁₆Mg₃₂Zn₅₂, o Ti₄₅Zr₃₈Ni₁₇.
I primi campioni prodotti avevano dimensioni micrometriche ed erano termodinamicamente instabili. Oggi diverse fasi quasi-cristalline possono essere prodotte in campioni di dimensioni dell'ordine di grandezza di 1 mm o anche di 1 cm mediante tecniche convenzionali per la crescita di monocristalli. Questi campioni mostrano spesso delle facce ben sviluppate corrispondenti a solidi, come il dodecaedro, di simmetria icosaedrica. Quasi contemporaneamente alle fasi icosaedriche sono stati scoperti q.-c. con assi di simmetria 'proibiti' di ordine 8 (V₁₅Ni₁₀Si), 10 (Al₇₀Co₂₀Ni₁₀) e 12 (V₃Ni₂). Questi consistono di strati quasi-cristallini accatastati periodicamente lungo l'asse di simmetria.
Per descrivere la disposizione degli atomi nei q.-c. sono stati sviluppati nuovi modelli strutturali, anche se inizialmente ha avuto un certo peso la posizione assunta da L. Pauling, che sosteneva che l'apparente simmetria anomala dei q.-c. poteva essere attribuita alla presenza di geminati multipli di cristalli cubici.
Descrizione della struttura
La struttura dei cristalli ordinari può essere descritta nel modo più conveniente come la ripetizione periodica di una cella unitaria, decorata da un insieme di atomi (base), in modo da formare un ricoprimento (tiling) di tutto lo spazio. Questo metodo può essere usato anche per descrivere le strutture dei q.-c., con la differenza che sono necessarie almeno due celle unitarie.
L'esempio più semplice, peraltro molto utile, di ricoprimento quasi-periodico è fornito dalla catena di Fibonacci: si tratta del ricoprimento di una retta mediante due segmenti, uno lungo (L) e uno corto (S), ripetuti secondo una ben determinata legge aperiodica, per es. L, LS, LSL, LSLLS, LSLLSLSL, LSLLSLSLLSLLS, ...... in cui il generico termine si ottiene riproducendo in sequenza i due precedenti nell'ordine. Si può dimostrare che al tendere della lunghezza della catena all'infinito, il rapporto n(L)/n(S) fra il numero di L e di S contenuti nella catena tende alla sezione aurea
τ=(1+ 5)/2≈̳1,618034 ..... (per i termini rappresentati sopra si ha rispettivamente τ=∞, 1, 2, 3/2, 5/3, 8/5). Corrispondentemente la trasformata di Fourier della catena contiene due frequenze spaziali fondamentali k₁ e k₂ il cui rapporto è τ. In conseguenza del fatto che k₁/k₂ è irrazionale sussistono tre proprietà caratteristiche che risultano valide per tutti i q.-c., e cioè:
a) le frequenze spaziali n₁k₁+n₂k₂ con n₁ e n₂ interi sono indicizzate da un numero di interi (due) maggiore della dimensione dello spazio (una);
b) le frequenze costituiscono un insieme numerabile e denso nello spazio reciproco;
c) le corrispondenti lunghezze d'onda non hanno un multiplo comune e pertanto la catena non può essere periodica.
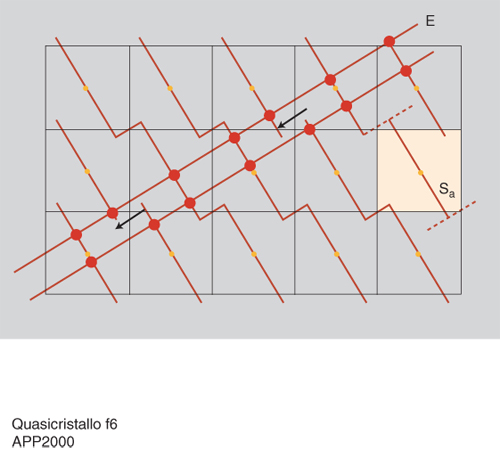
Un modello bidimensionale è fornito dal ricoprimento di Penrose (fig. 3), proposto circa otto anni prima della scoperta dei q.-c., come un esempio di ricoprimento aperiodico del piano mediante due mattonelle. Queste sono un rombo 'grasso' e un rombo 'magro' presenti nel rapporto τ. Gli angoli sono multipli di 2π/10 e pertanto il ricoprimento ha in media un asse di simmetria di ordine 10. Per ottenere la quasi-periodicità le mattonelle devono essere aggiunte seguendo regole fisse negli accostamenti. Un'estensione a un ricoprimento tridimensionale, avente in media la simmetria icosaedrica, è stato elaborato da T. Ammann e P. Kramer con due tipi di romboedri come celle unitarie.
I ricoprimenti quasi-periodici mostrano numerose proprietà caratteristiche comuni: le strutture locali si ripetono, seppure non periodicamente; posseggono proprietà di scala, vale a dire che se unità strutturali sono contenute in strutture più grandi, queste a loro volta compongono strutture ancora più grandi in cui sono contenute in maniera simile; i vertici delle celle unitarie appartengono a famiglie di piani paralleli separati da un numero finito di distanze che si ripetono in modo quasi-periodico. I modelli atomici strutturali si ottengono, come nel caso dei cristalli ordinari, decorando le celle unitarie, cioè ponendo vari tipi di atomi ai vertici, lungo gli spigoli, o nei punti medi delle diagonali. Questi modelli strutturali possono essere costruiti come sezioni di cristalli ordinari, ma di dimensioni più grandi.
Per es., per un q.-c. unidimensionale come la catena di Fibonacci il cristallo ordinario è bidimensionale (perché ci sono due frequenze fondamentali nella trasformata di Fourier, fig. 4). A ciascun atomo di un reticolo quadrato è associata una superficie (qui un segmento). Tutte queste superfici atomiche sono parallele e ortogonali allo spazio sezione E che in questo caso è una retta di coefficiente angolare 1/τ. Le intersezioni di E con le superfici atomiche forniscono i punti della catena di Fibonacci.
Questo metodo della sezione è utilizzato in pratica per la determinazione della struttura dei q.-c. reali a partire dai dati di diffrazione di raggi X. Nel caso dei q.-c. icosaedrici, il reticolo ordinario che viene sezionato è un reticolo cubico a sei dimensioni, mentre le superfici atomiche sono complicati poliedri. Le posizioni degli atomi del q.-c. si ottengono quindi sezionando il reticolo cubico con un iperpiano a sei dimensioni. Il metodo della sezione può essere utilizzato anche per mettere in risalto l'esistenza nei q.c. di un nuovo grado di libertà per il moto degli atomi, detto fasone, corrispondente a uno spostamento dello spazio sezione E parallelamente a se stesso. Durante questo movimento E abbandona certe superfici atomiche e ne interseca altre, con il risultato che i vertici eseguono un moto a salti (phason flip) all'interno di certe gabbie (fig. 4). Per la catena di Fibonacci la gabbia è un segmento LS, mentre nel ricoprimento di Penrose è un esagono formato da tre mattonelle (fig. 3). Di regola un singolo salto fasonico risistema le mattonelle adiacenti in maniera tale che risultano violate le regole di raccordo. Con una sequenza di salti fasonici i vertici possono essere trasportati attraverso distanze arbitrarie. Con un numero sufficientemente grande di salti fasonici un ricoprimento quasi-periodico può essere trasformato in un ricoprimento disordinato (random), in cui lo spazio è ancora totalmente ricoperto senza lacune o sovrapposizioni, ma in maniera irregolare. Per ottenere un cristallo quasiperiodico mediante il metodo della sezione, l'iperpiano sezione E deve toccare il reticolo multidimensionale al più in un punto. Se E è inclinato in modo da toccare l'iperreticolo in due (e quindi infiniti) punti, con il metodo della sezione si ottiene un cristallo periodico che è chiamato l'approssimante razionale del quasi-cristallo. A ogni fase quasi-cristallina si possono associare in questo modo cristalli approssimanti. Più è accurata l'approssimazione nel riprodurre la struttura locale del q.-c. e più grande è la cella unitaria dell'approssimante. Retrospettivamente si può dire che la proposta originaria di Pauling, sopra citata, trova la sua giustificazione in questa circostanza. I q.-c. possiedono piani atomici regolari; tuttavia la struttura può essere vista pure in termini di un modello gerarchico a grappoli (cluster). Per es., per i sistemi Al-Pd-Mn i mattoni fondamentali sono cluster di 54 atomi con un diametro di 1 nm, consistenti in tre gusci sferici di simmetria icosaedrica, denominati Mackey-cluster. I cluster possono essere considerati come atomi di super-cluster e questi a loro volta come atomi di super-super-cluster.
Proprietà fisiche
I q.-c. reali appaiono in un piccolo intervallo di concentrazioni del diagramma di fase di sistemi binari. Per questo intervallo il numero di elettroni di valenza per atomo (calcolato dalla valenza dei costituenti) è costante; per es., per Al-Cu-Fe è 1,75. Da questa osservazione si è dedotto che la maggior parte dei q.-c. è stabilizzata secondo la regola di Hume-Rothery, cioè la sfera di Fermi tocca il bordo di una delle zone di Brillouin: si formano dei salti di energia (gap) e diminuisce l'energia elettronica totale. Una prova sperimentale di questa ipotesi è l'osservazione di una pseudo-gap all'energia di Fermi in misure di emissione e assorbimento di fotoelettroni. Un ulteriore meccanismo che produrrebbe la stabilità dei q.-c. è la cosiddetta stabilizzazione entropica, consistente nel fatto che ad alte temperature T possono essere facilmente eccitati i salti fasonici che producono un aumento dell'entropia S del q.-c. e una corrispondente riduzione dell'energia libera F=U-TS con U energia interna. In effetti l'intervallo di stabilità dei q.-c. si restringe al diminuire della temperatura e parecchi q.-c. corrispondono ad aggregati atomici disordinati ad alta temperatura.
Per quanto riguarda le proprietà elettroniche, calcoli su modelli provano che la maggior parte degli stati elettronici non è costituita da stati localizzati, che decadono cioè esponenzialmente con la distanza, né da stati estesi, ma da stati critici caratterizzati da un decadimento con legge di potenza. Questa criticità è facilitata dalla struttura a cluster. Il trasporto elettronico avviene con un moto a salti fra stati critici; inoltre, a causa della pseudo-gap all'energia di Fermi, il numero di elettroni di valenza è minore di quello dei metalli puri. Entrambi questi effetti portano a una conducibilità di tipo semimetallico e quasi semiconduttore (dell'ordine di 1Ω⁻¹cm⁻¹ alla temperatura di pochi kelvin). La conduttività cresce esponenzialmente o con legge di potenza fino alla temperatura di fusione e diminuisce con la qualità strutturale, in sorprendente contrasto con il comportamento metallico usuale. I fononi, sebbene si propaghino nei q.-c. a basse frequenze, diventano localizzati ad alte frequenze, trasformandosi probabilmente in vibrazioni dei cluster. Pertanto, un'altra proprietà di trasporto, la conducibilità termica, è bassa (∼1 Wm⁻¹K⁻¹). Al crescere della temperatura mostra un plateau simile a quello osservato nei metalli amorfi. Il contributo delle vibrazioni reticolari al calore specifico è molto piccolo, per cui questa quantità è dominata dal contributo degli elettroni, ma la dipendenza dalla temperatura devia dalla linearità usuale nei metalli ed è in accordo con una legge di potenza. A causa del meccanismo a salti dovuto ai fasoni ci si aspetterebbe un'elevata diffusività, ma gli esperimenti non confermano questa previsione.
I q.-c. mostrano un comportamento particolare anche rispetto alle proprietà meccaniche. A temperatura ambiente sono duri come il silicio e quasi altrettanto fragili. A circa il 70% della temperatura di fusione (∼1000 K) diventano plastici senza presentare indurimento, cioè a parità di deformazione si richiede uno sforzo minore. Nei cristalli il meccanismo della deformazione plastica è la migrazione delle dislocazioni. Le dislocazioni esistono anche nei q.-c., ma quando si muovono sono seguite da una parete di salti fasonici, più o meno come una bandiera trasportata dall'asta. A basse temperature la parete fasonica rimane stretta indebolendo i legami chimici. Ad alte temperature le pareti fasoniche si allargano e creano vaste zone di slittamento (glide), lungo le quali possono enuclearsi coppie secondarie di dislocazioni che facilitano la deformazione plastica.
Applicazioni e prospettive
Le proprietà fisiche dei solidi sono determinate essenzialmente da due fattori: la composizione chimica e la struttura. Nei q.-c. la struttura sembra essere dominante. Abbiamo visto che per molti aspetti i q.-c. mostrano comportamenti anomali rispetto ai metalli, sebbene siano composti essenzialmente da atomi metallici. La ricerca corrente nei q.-c. ha numerosi obiettivi. In primo luogo, poiché piccolissime variazioni nella composizione provocano superstrutture e disordine, la determinazione delle strutture è estremamente difficile. Le posizioni degli atomi non sono state ancora determinate con precisione, e solo per tre o quattro sistemi esistono modelli strutturali approssimati. È necessario uno sforzo combinato di tutti i metodi per la determinazione delle strutture.
Dal punto di vista teorico manca ancora una descrizione coerente delle eccitazioni elementari; in particolare, una questione centrale è in che modo i fasoni si manifestano nella forma di moti atomici di salti correlati.
Esistono molti studi sulle potenziali applicazioni dei quasi-cristalli. La bassa densità degli elettroni di valenza associata alla durezza e a uno strato protettivo di ossido di alluminio rende i q.-c. candidati promettenti per coperture stabili a basso attrito.
Di regola queste coperture si ottengono producendo, mediante fusione ad arco, micro-q.-c. che vengono quindi spruzzati allo stato di plasma sulla superficie di materiali meno duri. A causa della bassa conducibilità termica questa superficie quasi-cristallina costituisce uno strato isolante che potrebbe essere usato, per es., nei cilindri dei motori riducendo così le perdite di energia e consentendo di eliminare costosi dispositivi di raffreddamento. Poiché molti q.-c. si basano sull'alluminio, hanno una bassa densità, proprietà che potrebbe tornare utile in molti casi se non fosse associata a una notevole fragilità a temperatura ambiente e a temperature più basse. Questa deficienza può essere notevolmente attenuata includendo grani icosaedrici di dimensioni dell'ordine del nanometro, in una matrice cristallina. Il risultato è un materiale leggero con ottime proprietà meccaniche. In un acciaio commerciale usato per fabbricare strumenti chirurgici sono stati scoperti precipitati quasi-cristallini che rendono la lega molto resistente. Inoltre, particelle nanometriche di AlCuFe immerse in una matrice dielettrica, come Al₂O₃, assorbono luce nel visibile e la emettono nell'infrarosso così che potrebbero essere utilizzate come assorbitori solari selettivi.Q.-c. icosaedrici a base di Ti possono immagazzinare 1,9 atomi di idrogeno per atomo-ospite. Questa proprietà deriva dal fatto che un icosaedro è composto da 20 tedraedri leggermente distorti e l'idrogeno può essere catturato in queste gabbie tetraedriche.
Vista l'intensità della ricerca applicata sui materiali quasi-cristallini in tutto il mondo, non sembra azzardato predire che essi diventeranno presto prodotti comuni della vita di tutti i giorni.
bibliografia
Ch. Janot, Quasicrystals: a primer, Oxford-New York 1992; Lectures on quasicrystals, ed. F. Hippert, Les Ulis 1994; New horizons in quasicrystals: research and applications, ed. A.J. Goldman et al., Singapore-River Edge (N.J.) 1997.