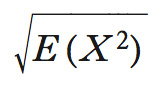quadratico
quadratico
Relativo all’elevazione a quadrato. In generale, nel linguaggio scientifico e tecnico, indica un legame tra due variabili o tra due grandezze fisiche, espresso da una relazione di 2° grado (per es., espressione q., legge q. ecc.; misuratore q., rivelatore q ecc.).
Matematica. In matematica e nelle applicazioni, è usato con differenti accezioni aventi un significato particolare. ● Le equazioni q. sono quelle algebriche di secondo grado, o anche quelle algebriche di grado potenza di 2, la cui soluzione sia riconducibile a quella di equazioni di secondo grado. ● La trasformazione q. è una funzione che al valore di una variabile x associa un polinomio di secondo grado di x.
La forma q. è un polinomio omogeneo di secondo grado in più variabili. Se queste si indicano con x1,...,xn, una forma q. f si scrive: f=a11x12+a22x22+...+annxn2+2a12x1x2+...+2an−1,nxn−1xn, dove si suppone che sia aik=aki. In forma matriciale (➔ matrice), quindi in maniera più compatta, possiamo notare come f=x′Ax, dove ai,,j è il generico elemento della matrice quadrata e simmetrica A, mentre x è il vettore colonna x=(x1,...,xn)′ (➔ vettore).
La media q., per un numero finito di termini, è la radice quadrata di quella aritmetica dei quadrati dei termini; è perciò una media di potenze di ordine due. Per una variabile aleatoria X, è la radice quadrata del momento di ordine 2, cioè:
Per lo scarto q. medio ➔ deviazione standard.
L’errore q. medio: in inglese (MSE, Mean Squared Error) è la misura dell’efficienza di uno stimatore (➔ efficienza statistica; stimatore) definita come momento secondo della differenza tra questo e il parametro (➔) da stimare. Se per es. θ è un parametro scalare e θ^ uno stimatore per θ, MSE(θ^)=E(θ^−θ)2.
Le funzioni q. sono concave (o convesse), il che rende particolarmente semplice trovare il punto di massimo (rispettivamente di minimo). Per questo motivo vengono spesso usate in economia, per modellare l’utilità, funzioni di domanda o di costo, o altri tipi di funzioni per le quali la teoria economica richiede la soluzione di un problema di ottimizzazione (➔ funzione matematica).