punto singolare

punto singolare

punto singolare per una linea espressa da un’equazione in forma implicita ƒ(x, y) = 0 è un punto in cui gradƒ = 0, avendo indicato con gradƒ il gradiente della funzione scalare ƒ. La classificazione dei punti singolari si esegue osservando la → matrice hessiana di ƒ nel punto. Se il suo determinante è positivo, il punto è un punto doppio isolato: ciò significa che l’equazione non ammette altre soluzioni in un intorno del punto stesso. Se il determinante hessiano è negativo, si tratta di un → nodo: esso è un punto (x₀, y₀) in cui si intersecano due rami. Se essi hanno equazione y = y_k(x) (con k = 1,2), con y_k(x₀) = y₀, ciascuno di essi può essere studiato procedendo come per le funzioni implicite. Dall’identità ƒ(x, y_k(x)) = 0 si ottiene, derivando,

che non dà informazioni, essendo per ipotesi ƒ_x(x₀, y₀) = f_y(x₀, y₀) = 0. Derivando ulteriormente si ha

Sostituendovi le coordinate di (x₀, y₀) e ricordando che f_y(x₀, y₀) = 0 si ha l’equazione

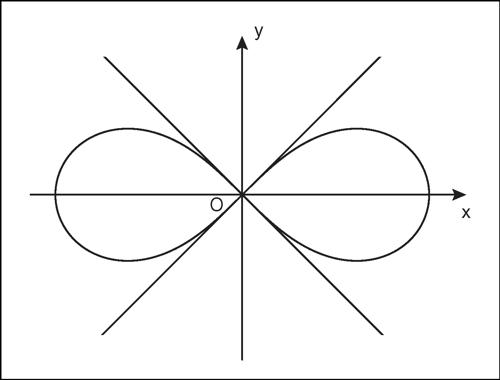
Questa è un’equazione di secondo grado che ammette come discriminante l’hessiano di ƒ cambiato di segno: ha dunque, in questo caso due radici reali distinte che forniscono i coefficienti angolari y_k′(x₀) dei due rami. Procedendo ulteriormente, se ƒ è sufficientemente regolare, si possono ottenere le derivate successive delle funzioni y_k(x). Per esempio, la lemniscata di Bernoulli (x ² + y ²)² = 2a²(x ² − y ²) ammette nell’origine un punto doppio nodale. Derivando l’identità (x ² + y(x)²)² − 2a(x ² − y(x)²) = 0 si ha

sostituendo x = 0 e y(0) = 0 si ottiene 0 = 0. Derivando ancora e sostituendo nuovamente x = 0 e y(0) = 0 si ottiene però 2 − 2y ′(0)² = 0, da cui i coefficienti angolari y ′(0) = ±1 dei due rami. Proseguendo in modo analogo si ricava che per entrambi risulta y ″(0) = 0, mentre proseguendo si trova y ‴(0) = ±6/a, da cui si deduce che entrambi i rami hanno un flesso nell’origine, discendente per il ramo crescente e ascendente per quello decrescente.

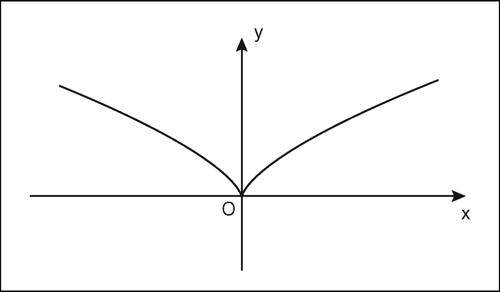
Il caso dell’hessiano nullo è più difficile, e salvo situazioni particolari, deve essere studiato caso per caso. La configurazione più semplice è quella di una → cuspide, per esempio quella che rappresenta il grafico della relazione x ² − y ³ = 0 che dà luogo alla funzione y = x ^2/3.