punti coniugati

punti coniugati

punti coniugati due punti P e P′ del piano o dello spazio legati da una relazione di coniugio, una relazione che sia cioè simmetrica e involutoria. La locuzione è pertanto generica e va precisata ulteriormente. Due punti del piano possono infatti essere coniugati rispetto a una → polarità definita da una curva del piano, per esempio da una conica (la nozione si estende a spazi di dimensione n > 2 ed è stabilita quando ciascuno dei due punti passa per la polare dell’altro). Rispetto a una → quadrica, due punti sono coniugati se dividono armonicamente le intersezioni della loro congiungente con la superficie. La relazione così stabilita è simmetrica; inoltre, su una retta dello spazio che non appartenga alla superficie, esistono infinite coppie di punti coniugati, le quali danno una involuzione avente come punti autoconiugati le intersezioni con la superficie quadrica (→ coniugio). Se due punti sono coniugati rispetto a una quadrica, l’uno appartiene al piano polare dell’altro rispetto a essa.

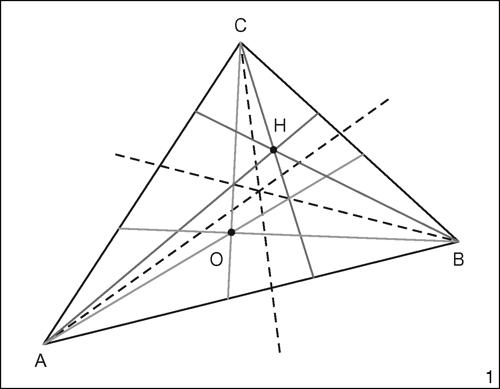
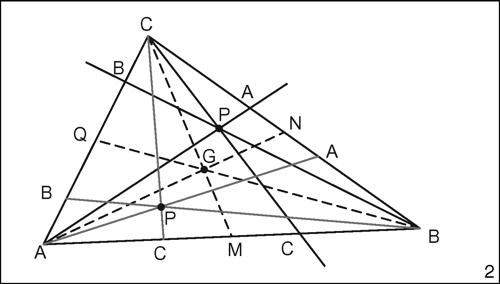
Punti coniugati in un triangolo

Due punti interni a un triangolo si dicono coniugati isogonali quando le rette che li congiungono ai vertici sono simmetriche rispetto alle bisettrici del triangolo. Oppure ancora, due punti si dicono coniugati isotomici quando le rette che li congiungono ai vertici intersecano i lati opposti in punti simmetrici rispetto ai punti medi dei rispettivi lati del triangolo.