prova del nove
prova del nove
prova del nove algoritmo che fornisce una condizione, necessaria ma non sufficiente, per verificare l’esattezza del risultato in un’operazione aritmetica tra numeri interi (vale a dire la moltiplicazione, l’addizione, la sottrazione e la divisione con resto).
L’algoritmo permette di ricondurre la verifica a operazioni che coinvolgono numeri relativamente piccoli e pertanto applicare la prova del nove può essere più semplice che non verificare i passi mediante i quali è stato calcolato il presunto risultato.
L’algoritmo si fonda sull’uso della → radice digitale di un numero (cioè la somma delle cifre del numero eventualmente ripetuta sul risultato fino a ottenere un numero di una cifra) e deve il suo nome al fatto che, modulo 9, la radice digitale di un numero è congruente con il numero stesso.
Nel caso di una moltiplicazione n ⋅ m, di cui si vuole verificare il risultato r, l’algoritmo consiste allora nel calcolare le radici digitali dei fattori e del presunto risultato, che si indicano rispettivamente con i simboli R[n], R[m] e R[r]: se il risultato r è corretto, allora deve essere verificata la condizione R[R[n] ⋅ R[m]] = R[r], vale a dire la radice digitale del prodotto delle radici digitali dei fattori deve essere uguale alla radice digitale del risultato.
Tipicamente, nell’esecuzione dell’algoritmo ci si serve di uno schema a croce del tipo
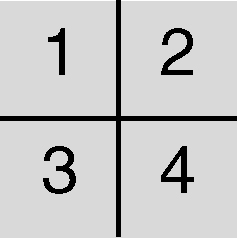
in cui si numerano i quadranti come segue
In tale schema sono disposti, nell’ordine e partendo dal primo quadrante, la radice digitale del primo operando, la radice digitale del secondo operando, la radice digitale del presunto risultato. Si calcola dunque la radice digitale del prodotto delle entrate sulla prima riga dello schema e la si scrive nell’ultimo quadrante. Se il risultato è corretto, allora le entrate sulla seconda riga devono coincidere.
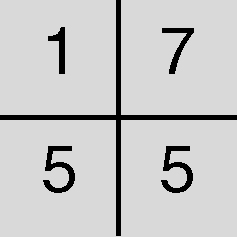
Data per esempio la moltiplicazione 1237 ⋅ 456 si verifica che il risultato 564074 non è corretto: la radice digitale di 1237 è 4, quella di 456 è 6, quella di 564074 è 8; infine la radice digitale di 24 = 4 ⋅ 6 è 6. Quindi si ottiene
e pertanto il risultato è sbagliato. Si verifica invece che 564072 “può essere” il risultato corretto: infatti la sua radice digitale è 6, si ottiene
e la prova del nove dà esito positivo. In effetti 564072 = 1237 ⋅ 456 è il risultato corretto, ma tale affermazione non può essere dedotta dall’algoritmo.
La prova del nove funziona in modo analogo nel caso dell’addizione e della sottrazione. Nel caso della divisione con resto l’algoritmo deve invece essere leggermente modificato. In questo caso bisogna inserire nel primo quadrante la radice digitale del divisore, nel secondo quadrante quella del quoziente, nel terzo quadrante quella del dividendo e, nel quarto quadrante, la radice digitale della somma del resto con il prodotto delle entrate sulla prima riga. Se il risultato è corretto, allora le entrate sulla seconda riga devono coincidere. Per esempio si supponga che nella divisione 11570 : 451 si sia calcolato 25 come quoziente intero e 295 come resto. L’algoritmo dà esito positivo (in effetti il risultato è corretto): la radice digitale di 451 è 1, quella di 25 è 7, quella di 11570 è 5, quella di 302 = 295 + 7 ⋅ 1 è 5, dunque si ottiene