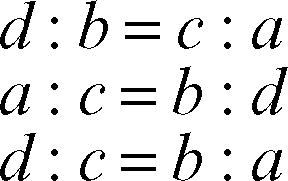proporzione

proporzione

proporzione uguaglianza fra due rapporti. Tipicamente una proporzione è espressa nella forma a : b = c : d, che si legge «a sta a b come c sta a d»; in modo equivalente essa può essere espressa come uguaglianza tra frazioni nella forma a /b = c /d. I numeri a, b, c, d sono detti termini della proporzione; più in particolare essi sono denominati in modo diverso a seconda del posto che occupano: nella proporzione a : b = c : d gli antecedenti sono i numeratori dei rapporti (a e c), i conseguenti sono i denominatori (b e d); b e c si dicono medi, a e d sono gli estremi della proporzione. Segue immediatamente dalla definizione la proprietà fondamentale delle proporzioni: se vale a : b = c : d allora sussiste l’uguaglianza ad = bc, vale a dire, il prodotto dei medi è uguale a quello degli estremi.

Una proporzione si dice geometrica (o continua) quando i medi sono uguali; essa è cioè una proporzione della forma a : m = m : b. Il termine m viene detto allora medio proporzionale (o media geometrica) tra a e b. Dalla proprietà fondamentale delle proporzioni, segue che in una proporzione geometrica il medio proporzionale è uguale a √(ab). Nella scuola pitagorica, accanto alle proporzioni geometriche, si distinguevano anche le proporzioni aritmetiche (le quali non sono proporzioni nel senso moderno del termine), in cui si considera un’uguaglianza tra due differenze del tipo a − m = m − b, e le proporzioni armoniche, della forma (m − a) : a = (b − m) : b. Il termine medio m di una proporzione aritmetica è detto media aritmetica tra a e b e vale m = (a + b)/2; il numero m che compare in una proporzione armonica è invece detto media armonica tra a e b e vale m = 2ab /(a + b). Dati quattro numeri non nulli a, b, c, d, si dice anche che essi costituiscono una proporzione armonica quando i loro reciproci sono in proporzione aritmetica, ossia quando 1/a − 1/b = 1/c − 1/d.

Le principali proprietà di una data proporzione a : b = c : d sono espresse dalle seguenti regole:

• regola del quarto proporzionale: noti tre termini di essa, è allora noto anche il quarto. Per esempio, se vale a : b = c : d e sono noti a, b e c, allora d = bc /a;

• regola dell’invertendo: si ottiene un’altra proporzione scambiando tra di loro gli antecedenti e i conseguenti all’interno dei due membri dell’uguaglianza. Se vale a : b = c : d, allora vale anche b : a = d : c;

• regola del permutando: si ottiene un’altra proporzione scambiando tra di loro gli estremi, i medi o entrambi. Se vale a : b = c : d, allora valgono anche:

• regola del componendo: si ottiene un’altra proporzione scambiando in un membro l’antecedente con la somma degli antecedenti e il conseguente con la somma dei conseguenti. Se vale a : b = c : d, allora valgono anche:

• regola dello scomponendo: si ottiene un’altra proporzione scambiando in un membro l’antecedente con la differenza degli antecedenti e il conseguente con la differenza dei conseguenti. Se vale a : b = c : d, allora valgono anche: