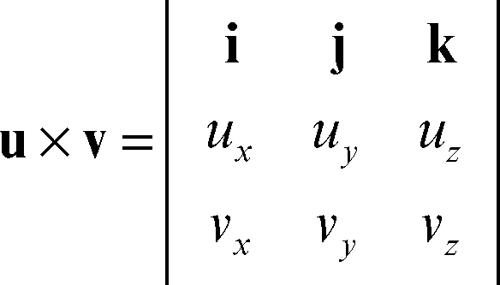prodotto vettoriale

prodotto vettoriale

prodotto vettoriale nell’ordinario spazio euclideo tridimensionale R³, inteso come spazio vettoriale V₃, legge di composizione binaria tra vettori il cui risultato è un vettore dello stesso spazio. Tale operazione, detta anche prodotto vettore o prodotto esterno, è quindi una applicazione V₃ × V₃ → V₃. Dati due vettori u = (u_x, u_y, u_z) e v = (v_x, v_y, v_z), il loro prodotto vettoriale, indicato con u × v (oppure con u ∧ v, e si legge «u vettore v») è il vettore che ha come modulo |u| ⋅ |v| ⋅ sinθ, essendo θ l’angolo (minore) formato dai due vettori, come direzione la direzione perpendicolare a quella del piano dei due vettori e come verso quello di un vettore w tale che la terna ordinata (u, v, w) sia concorde con la base {i, j, k} (sia cioè destrogira o levogira concordemente con quest’ultima). Il prodotto vettoriale ha molte applicazioni in fisica; è tale per esempio il momento di una forza rispetto a un punto. In tale contesto, in un sistema di riferimento dello spazio destrogiro, un metodo pratico per determinare la direzione e il verso del prodotto vettoriale è costituito dalla cosiddetta regola della mano destra: allineando il pollice di tale mano nella direzione e nel verso del primo vettore, l’indice nella direzione e verso del secondo vettore, il medio, tenuto perpendicolare alle altre due dita, fornisce la direzione e il verso del prodotto vettoriale.

Le componenti del prodotto vettoriale possono essere espresse in funzione delle componenti dei vettori fattori u × v = (u_yv_z − u_zv_y, u_zv_x − u_xv_z, u_xv_y − u_yv_x), che è esprimibile anche come sviluppo del determinante:

Nello spazio ordinario, il modulo del prodotto vettoriale è uguale all’area del parallelogramma individuato dai due vettori. Il modulo di tale prodotto risulta pertanto massimo quando i due vettori sono perpendicolari, minimo, cioè nullo, quando sono paralleli. Due vettori sono quindi linearmente indipendenti se e solo se il loro prodotto vettoriale è diverso da zero. L’operazione di prodotto vettoriale non è né associativa, né commutativa, ma gode delle seguenti proprietà:

• u × v = − v × u

(proprietà anticommutativa)

• u × (v + w) = u × v + u × w

(proprietà distributiva)

• u × (v × w) + v × (w × u) + w × (u × v) = 0

(identità di Jacobi)

Il prodotto vettoriale non dipende dal riferimento scelto, ma soltanto dal suo orientamento. Per i versori degli assi coordinati valgono le relazioni: i × j = k, j × k = i, k × i = j.