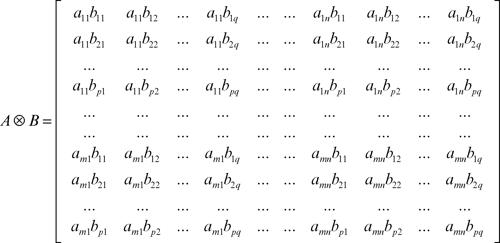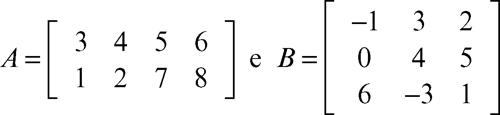prodotto tensoriale

prodotto tensoriale

prodotto tensoriale in algebra lineare, la più generale struttura dotata di applicazione bilineare che può riferirsi a vettori, matrici, moduli, spazi vettoriali.

Prodotto tensoriale di spazi vettoriali

Relativamente a due spazi vettoriali V e W di dimensione finita su un campo K, è uno spazio vettoriale T dotato di un’applicazione bilineare ⊗: V × W → T che soddisfa la seguente proprietà universale:

• se U è uno spazio vettoriale su K dotato di un’applicazione bilineare ƒ: V × W → U, allora esiste unica un’applicazione lineare ƒ *: T → U tale che per ogni coppia (v, w) ∈ V × W si abbia

Uno spazio vettoriale T che soddisfi tale proprietà esiste sempre ed è univocamente definito da essa; esso è detto il prodotto tensoriale di V per W ed è indicato con il simbolo V ⊗ W. Se {v₁, …, v_n} è una base di V e {w₁, …, w_m} è una base di W, allora {v_i ⊗ w_j, i = 1, …, n, j = 1, …, m}, inteso come un insieme di mn simboli formali, è una base di V ⊗ W, il quale ha per dimensione il prodotto delle dimensioni di V e W.

V ⊗ W è dunque lo spazio vettoriale su K costituito da tutte le combinazioni lineari formali del tipo

dove a_ij ∈ K.

Se v = x₁v₁ + … + x_nv_n e w = y₁w₁ + … + y_mw_m, allora

è il prodotto tensoriale di v e w. Con gli opportuni accorgimenti, la nozione si estende al prodotto tensoriale di moduli su anelli. Per il prodotto di tensori si veda → tensore.

Prodotto tensoriale di matrici

Date due matrici A_m,n e B_p,q, il loro prodotto tensoriale o prodotto di Kronecker, indicato con A ⊗ B, è la matrice mp × nq così definita:

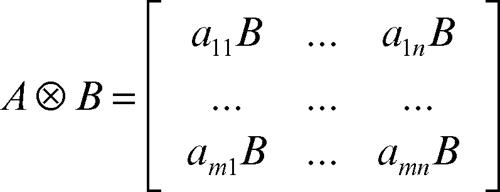
Riscrivendo la matrice prodotto a blocchi si ha:

Per esempio, date le due matrici:

il loro prodotto tensoriale è: