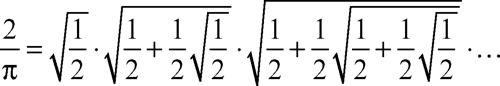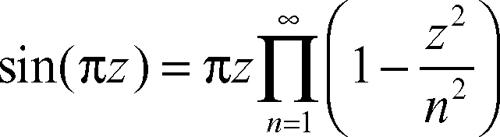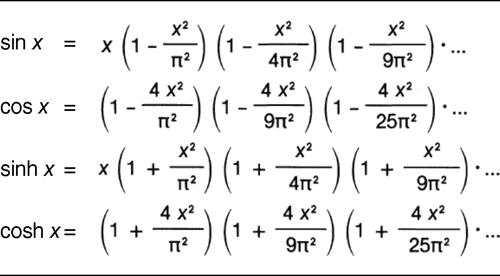prodotto infinito

prodotto infinito

prodotto infinito prodotto di un numero non finito di fattori, indicato con l’estensione all’infinito del simbolo di → produttoria (o moltiplicatoria)

che indica il prodotto degli n +1 fattori

I primi prodotti infiniti sono stati utilizzati per ottenere approssimazioni di π. Il primo in assoluto è dovuto a F. Viète, che usando il metodo di Archimede a partire dal quadrato inscritto in una circonferenza, trovò nel 1646 la formula

J. Wallis nel 1655 ottenne la formula che porta il suo nome:

Un prodotto infinito è, quindi, la generalizzazione della nozione di prodotto a un numero infinito di fattori, come le serie lo sono della somma per un numero infinito di addendi. Esso è rappresentato da un’espressione della forma

da intendersi come

Poiché un prodotto si annulla se uno dei fattori (che costituiscono una successione) è nullo, si suppone in genere ∀n (u_n ≠ 0). Sotto tale ipotesi si dice che il prodotto infinito è convergente (in senso stretto) se il limite indicato è finito e diverso da 0; se tale limite è infinito o nullo si dice che il prodotto diverge (a ∞ o a 0); un prodotto infinito si dice inoltre oscillante se né è convergente né diverge a infinito. Un condizione necessaria per la convergenza è che u_n → 1 per n → ∞. Tale condizione non è però sufficiente: per esempio, il prodotto

diverge a 0 pur non avendo alcun fattore nullo e pur essendo

Se si pone u_n = 1 + a_n, gli a_n si chiamano termini del prodotto infinito e la condizione necessaria per la convergenza è che a_n → 0 per n → ∞. Si dimostra che un prodotto a termini positivi converge se e solo se converge la serie

Per un prodotto a termini di segno qualsiasi la convergenza è garantita se e solo se converge la serie

dove N è un indice tale che |a_n| < 1 per n > N. Le precedenti equivalenze consentono di tradurre al contesto dei prodotti infiniti i criteri di convergenza per serie. Come esempi, sono degni di nota:

che generalizza la formula ottenuta con metodo di → Viète (per pi greco) e, nel campo complesso,

Quest’ultimo sviluppo è un caso particolare di una formula di → Weierstrass, che esprime mediante un prodotto infinito una qualsiasi funzione trascendente intera avente come zeri gli elementi di una successione {c_n} di numeri complessi, il cui unico punto di accumulazione sia z = ∞. Un altro importante prodotto infinito, che è ancora un caso particolare della formula di Weierstrass, è

in cui Γ è la funzione gamma di → Eulero e γ la costante di → Eulero (o Eulero-Mascheroni).