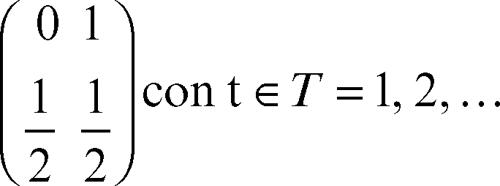processo stocastico

processo stocastico

processo stocastico successione di variabili aleatorie con la quale si rappresenta un sistema che si sviluppa nel tempo e nello spazio secondo leggi probabilistiche. Un processo stocastico è solitamente indicato con il simbolo {X_t; t ∈ T} dove X_t è la generica variabile aleatoria della successione, cioè la variabile che descrive i possibili valori al tempo t, e T è un insieme discreto o continuo. Le variabili X_t della successione possono essere continue o discrete e corrispondentemente il processo è detto continuo o discreto. Per esempio, se una moneta viene lanciata più volte e si realizza una vincita se la moneta mostra una testa (indicata con 1), la successione di variabili aleatorie X_t (con le rispettive probabilità)

costituisce un processo stocastico discreto, essendo le X_t variabili casuali discrete. In modo analogo, seT è continuo e, in particolare, è un intervallo, si parla di processo stocastico a parametro continuo, mentre se T è un insieme discreto si parla di processo stocastico a parametro discreto. Un esempio importante di processo stocastico a parametro continuo è costituito dalla distribuzione di → Poisson, impiegata quale modello probabilistico nello studio di svariati problemi di fisica legati a eventi casuali. Il più semplice esempio di processo stocastico a parametro discreto è costituito dalla passeggiata casuale o → random walk.

I valori via via assunti dalla variabile aleatoria sono detti stati del processo e l’insieme dei possibili stati è detto spazio degli stati. La successione delle osservazioni è detta realizzazione o storia del processo stocastico.

Nelle applicazioni si è spesso interessati al momento t in cui il processo stocastico entra per la prima volta in uno stato prefissato a. Lo stato prefissato è detto barriera assorbente e il tempo t in cui avviene il primo passaggio è chiamato tempo di assorbimento. A volte le barriere assorbenti sono due: una superiore e una inferiore e il processo ha termine non appena una barriera viene raggiunta.

Nei processi stocastici la probabilità dei diversi stati al tempo t può dipendere soltanto dallo stato assunto dal sistema nel tempo precedente oppure può dipendere da come si è arrivati allo stato del tempo precedente. Nel primo caso si parla di processo stocastico markoviano, mentre i secondi sono detti processi stocastici non markoviani. Se le probabilità dei diversi stati all’istante (t + s) dipendono soltanto da s e non da t, si dice che il processo stocastico è omogeneo. I processi stocastici markoviani omogenei e a parametro discreto sono detti catene di → Markov e hanno applicazioni particolarmente importanti.