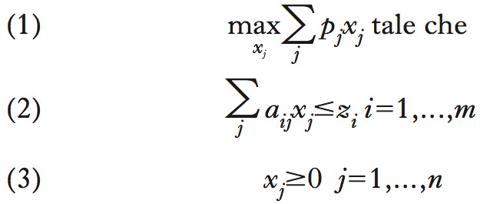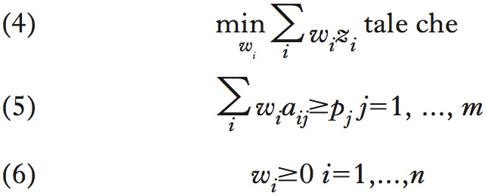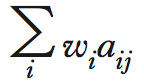duale, problema

duale, problema

Tipo di problema di ottimizzazione.

Ricerca operativa e problemi di ottimizzazione

La ricerca operativa (➔) ha sviluppato a livello teorico e di implementazione numerica metodi di soluzione per problemi di ottimizzazione (➔ ), lineare e non lineare, in presenza di vincoli di disuguaglianza e di un elevato numero di variabili. Fra gli argomenti per primi affrontati, particolare rilievo assumono i modelli di programmazione lineare, individuati dai seguenti 3 elementi: un insieme finito di disuguaglianze (o equazioni) lineari in un numero finito di incognite; vincoli di non negatività su tali incognite; una funzione lineare da massimizzare o minimizzare. Come indicato dal terzo punto, l’approccio si presta alla soluzione di problemi di ottimizzazione formulati sia in termini di massimizzazione sia di minimizzazione. Al problema di ottimizzazione, comunque formulato, che si indica come primario (o primale), è associabile un secondo problema di ottimizzazione, che si definisce d., in cui i ruoli di massimizzazione e minimizzazione vengono scambiati unitamente al segno di disuguaglianza dei vincoli.

Un esempio di problema duale

Si esamini, in concreto, il problema di massimizzazione dei ricavi di una compagnia petrolifera, che produce n output di raffinazione in quantità x₁, x₂, ..., x_n, con corrispondenti prezzi di mercato p₁, p₂, ..., p_n, e dispone di z₁, z₂, ..., z_m quantità di diversi tipi di greggio utilizzati come input nel processo di raffinazione. La tecnologia determina in modo rigido la quantità a_ij di ciascun input z_i (i=1, ..., m) necessaria per produrre un’unità di output x_j (j=1, ..., n). In termini analitici il problema di programmazione lineare è

In termini economici, la (1) rappresenta la funzione (i ricavi) da massimizzare, la (2) esprime il vincolo che l’utilizzo di ciascuna risorsa di greggio non può eccedere la relativa disponibilità e la (3) che non sono possibili produzioni negative. La soluzione del problema determina le quantità, positive o nulle, di ciascun output di raffinazione e quali input sono pienamente, o solo parzialmente, utilizzati nel programma ottimale. Il significato economico di quest’ultimo aspetto della soluzione è di particolare rilevanza. Gli input pienamente utilizzati costituiscono un vincolo effettivo alla massimizzazione dei ricavi; ove l’impresa disponesse di un’unità aggiuntiva di uno di essi, potrebbe accrescere i propri ricavi: ciascuno di questi input ha quindi un valore per l’impresa, desumibile marginalmente, per imputazione, dal maggiore ricavo così ottenibile. Per gli input non pienamente utilizzati, invece, un’eventuale maggiore disponibilità non potrebbe contribuire ad accrescere i ricavi; il loro valore per l’impresa è di conseguenza nullo.

Il problema d. ha come variabili da determinare proprio i valori, che si indicano come w_i, da attribuire alle risorse di cui l’impresa dispone ed è così formulato:

In termini economici, la (4) è la funzione (i costi) da minimizzare e la (6) la condizione di non negatività. Il senso della (5) è più complesso. La sommatoria

rappresenta il costo di produzione di un’unità del prodotto j; la (5) esprime quindi il vincolo che il costo di produzione non possa essere inferiore al prezzo unitario; in altri termini, impone la condizione che nessuna linea di produzione realizzi un profitto strettamente positivo. Infatti, se così fosse, data l’ipotesi di linearità della tecnologia, converrebbe produrre l’output considerato in una quantità infinitamente grande, ma ciò è palesemente impossibile. Se verificata con il segno di uguale, la (5) determina quindi quali output sono prodotti in quantità positive; se verificata, invece, con il segno di disuguaglianza, quali output non vengono prodotti. Si dimostra che nella soluzione ottimale l’ammontare dei ricavi è uguale a quello dei costi.