Cavalieri, principio di

Cavalieri, principio di

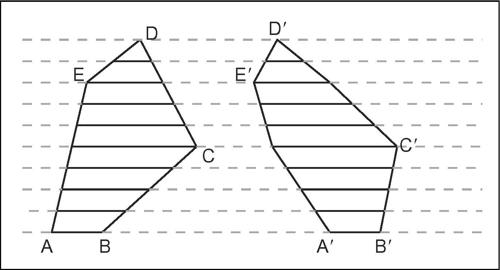
Cavalieri, principio di criterio che consente di stabilire se due superfici hanno la stessa area o due solidi hanno lo stesso volume. Il criterio fu utilizzato da B. Cavalieri nella prima metà del xvii secolo, anticipando metodi di calcolo infinitesimale che avrebbero ricevuto una sistemazione più rigorosa negli anni successivi, soprattutto per opera di G.W. Leibniz e I. Newton. In sostanza, il principio si basa sull’idea di pensare una figura piana come formata da un indeterminato numero di sottili fili paralleli e una figura solida come formata dalla sovrapposizione di infinitamente sottili fogli paralleli. Nel piano, il principio di Cavalieri afferma che se due figure, intersecate dalle rette di un fascio di parallele, danno luogo a sezioni (corde) della stessa lunghezza, esse sono equiestese, hanno cioè la stessa area.

Analogamente, nello spazio tridimensionale, il principio afferma che se ogni piano di un fascio di piani paralleli interseca due figure solide in due sezioni equiestese, allora i due solidi hanno lo stesso volume. Uno degli esempi più noti di applicazione del principio di Cavalieri consiste nel calcolo del volume della sfera, ottenuto confrontando il volume di un cono con quello della cosiddetta scodella di → Galilei. Il principio, che fornisce un criterio sufficiente ma non necessario per l’equiestensione, si basa sull’idea di indivisibile. Secondo la teoria degli indivisibili ogni figura piana è pensata come formata da particolari linee parallele, gli indivisibili, assimilabili a rettangoli aventi per base la corda e per altezza un segmento “piccolissimo”. Nel linguaggio moderno ogni indivisibile è una figura geometrica di spessore infinitesimo, rappresentabile con un prodotto del tipo ƒ(x)dx. Similmente, gli indivisibili di ogni figura solida sono sezioni del solido tra loro parallele, assimilabili a figure solide ottenute per traslazione “piccolissima” di una sezione e aventi un’altezza “piccolissima”. Il metodo degli indivisibili introdotto da Cavalieri riprende le idee di Archimede e pone le basi per lo sviluppo del calcolo integrale. Non essendo deducibile dagli assiomi dello spazio euclideo, il principio di Cavalieri è una sorta di assioma, che pone una condizione sufficiente, ma non necessaria, per l’equiestensione di due figure geometriche. Oggi è universalmente accettata la correttezza del principio, basata sulle formule di riduzione degli integrali multipli (→ coarea, formula di), ma al tempo di Cavalieri esso rimase fondato sul concetto assai vago di indivisibile.