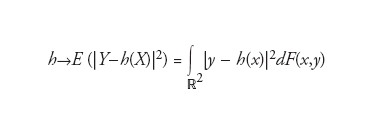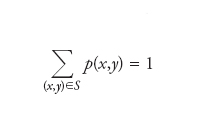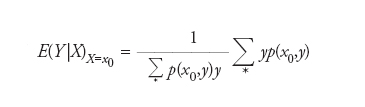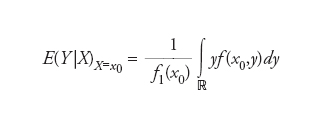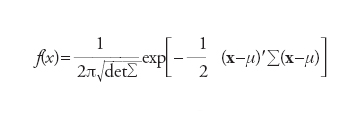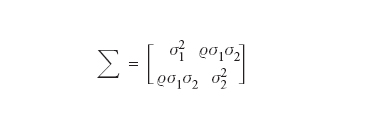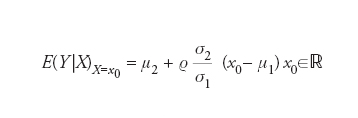principio della regressione

principio della regressione

Sia F la funzione di ripartizione, definita su ℝ², di una coppia (X,Y) di caratteri posseduti da ciascuna unità di una certa popolazione statistica. Si considerano quelle situazioni in cui un carattere, sia X per fissare le idee, è osservabile mentre risulta difficile, o non conveniente, procedere all’osservazione del secondo. Per es., se X e Y rappresentano, rispettivamente, il reddito e il consumo di una famiglia in un dato periodo, si può ritenere che il reddito possa essere rilevato con una relativa facilità e che, per contro, la determinazione del consumo richieda un’indagine più complessa, dall’esito altamente incerto. Si pone in questi casi il problema di come costruire una stima della determinazione di Y in corrispondenza di una determinazione di X: stimare il consumo di una data famiglia sulla base della conoscenza del suo reddito. Si può risolvere il problema costruendo una funzione h che a ogni possibile valore osservato di X associ un valore stimato Yˆ di Y. Come scegliere h? A questo fine si può partire dalla ovvia osservazione che la stima potrà essere affetta da errore e, quindi, mirare a scegliere h in modo da ridurre al minimo l’errore o, più concretamente, una congrua valutazione delle conseguenze dannose dell’errore stesso. Se tale valutazione porta a considerare l’errore quadratico medio (la radice quadrata, in senso aritmetico, del valore atteso del quadrato di |Y−Yˆ|), il problema sarà quello di ricercare un’espressione di h per la quale risulti minima la funzione

formula

Per essere più precisi, la questione viene posta sotto la condizione che Y abbia momento secondo finito (E(Y²)〈+∞) e che h abbia i necessari requisiti di misurabilità che fanno di h(X) un numero aleatorio. Una risposta completa al problema posto è contenuta nel seguente teorema: se E(Y²)〈+∞, allora un punto di minimo (assoluto) per l’errore quadratico medio [1], nella classe delle funzioni h per le quali h(X) è un numero aleatorio, è dato dalla speranza matematica condizionale E(Y|X) di Y dato X. Quando la distribuzione di (X,Y) è discreta (esistono un sottoinsieme numerabile S di ℝ² e una successione {p(x,y):(x,y)∈S} di numeri non negativi tali che

e, inoltre, P{X=x,Y=y}=p(x,y) per ogni (x,y) in S) allora, per ogni x₀ tale che P{X=x₀}>0, si ha

[2] formula

indicando ∑* la somma estesa ai numeri y per cui (x₀,y) appartiene a S. Invece, se F ha densità f (rispetto alla misura di Lebesgue in ℝ²), per ogni x₀ per cui f₁(x₀):=∫_ℝ f(x₀,y)dy>0 si ottiene

[3] formula

La [2] è di notevole importanza pratica essendo direttamente applicabile a distribuzioni empiriche e, quindi, anche ai risultati di indagini campionarie su specifici caratteri bidimensionali in una data popolazione statistica. La [3], invece, riguarderà prevalentemente modelli probabilistici di riferimento come, per es., quello gaussiano bidimensionale. Quest’ultimo è caratterizzato da una finzione di densità del tipo

[4] formula

in cui x=(x₁,x₂)∈ℝ², μ=(μ₁,μ₂) è un assegnato punto di ℝ² e

[5] formula

è una matrice definita postiva. In questo caso si ha

[6] formula

La funzione x₀→E(Y|X)_X=x0 che, in accordo con il teorema precedente, fornisce una soluzione del problema di stima formulato all’inizio, è anche nota come funzione di regressione di Y su X. Il teorema stesso viene talvolta richiamato come principio della regressione. Questa terminologia rimanda alle indagini pionieristiche degli statistici del XIX sec., che guardavano alla funzione di regressione come a uno strumento per lo studio della causalità nei fenomeni oggetto di osservazione. Non deve sfuggire, inoltre, il collegamento immediato fra principio della regressione e metodo dei minimi quadrati. Generalmente il calcolo della regressione presenta difficoltà e, quindi, si delimita la ricerca del minimo di [1] a sottoclassi proprie dell’insieme dei numeri aleatori h(X). Quando la classe prescelta è quella delle trasformazioni affini di X, allora si parla di regressione lineare. Ritornando al problema generale, si può notare che l’insieme dei numeri aleatori con momento secondo finito può essere riguardato come uno spazio di Hilbert L²(Ω,✄,P), (Ω,✄,P) denotando lo spazio di Kolmogorov su cui si suppongono definiti i numeri aleatori in questione. Allora, il sottoinsieme dei numeri aleatori h(X) espressi come funzione di un numero aleatorio X assegnato è un sottospazio lineare chiuso del precedente e, per ogni Y in L²(Ω,✄,P), E(Y|X) rappresenta la proiezione ortogonale di Y sul detto sottospazio.

→ Statistica