Previsioni del tempo
Previsioni del tempo
Prevedere il tempo è stato fin dall’antichità uno degli obiettivi dell’uomo per poter far fronte ai rischi che i fenomeni meteorologici comportano in tanti settori dell’attività economica e sociale. Le difficoltà incontrate hanno stimolato l’interesse di profani e studiosi, colpiti dall’evidente differenza tra i moti regolari degli astri e l’evoluzione capricciosa dell’atmosfera.
A partire dai primi decenni del Novecento, si è compreso che il metodo scientifico poteva essere applicato direttamente alla previsione meteorologica, purché si facesse ricorso a strumenti di calcolo che solo nella metà del secolo si sono resi disponibili, grazie all’enorme progresso dei calcolatori elettronici. Nel 1904 il grande meteorologo norvegese Vilhelm Bjerknes enunciò per la prima volta con chiarezza il principio, base della moderna previsione meteorologica, che definisce la previsione del tempo come un problema fisico ai valori iniziali. Scriveva infatti Bjerknes: «I fenomeni atmosferici si sviluppano da quelli che li precedono seguendo leggi precise, da cui consegue che le condizioni necessarie e sufficienti per effettuare una previsione meteorologica sono la conoscenza, con una precisione sufficiente, dello stato dell’atmosfera in un dato istante e la conoscenza delle leggi secondo cui uno stato dell’atmosfera si sviluppa a partire dallo stato precedente». Questa chiara enunciazione, se poneva i fondamenti teorici corretti della previsione meteorologica, ne preannunciava anche i limiti, derivanti sia dall’imperfetta conoscenza degli stati dell’atmosfera sia delle leggi che ne determinano l’evoluzione. Ma a quei tempi un ulteriore ostacolo si frapponeva all’attuazione della previsione basata esclusivamente su metodi matematici: le leggi del moto dell’atmosfera sono espresse mediante un sistema di equazioni differenziali non lineari alle derivate parziali, per il quale non si disponeva, né si dispone tuttora, di soluzioni generali analitiche.
Nella seconda metà del Novecento, via via che si sviluppavano modelli fisico-matematici sempre più complessi e cresceva la potenza informatica di cui essi potevano disporre, la meteorologia previsionale aumentava la propria accuratezzae allungava il periodo utile della previsione. Grandi centrimeteorologici nazionali e internazionali, come l’ECMWF (European Center for Medium range Weather Forecasting), iniziavano a emettere previsioni valide su tutto il globo, con parecchi giorni di anticipo utile.
A partire dagli anni Sessanta, la scienza dei sistemi complessi e caotici ha permesso sia di definire i limiti intrinseci della previsione meteorologica sia di migliorare le tecniche applicate all’assimilazione dei dati e alla previsione probabilistica. Si è quindi arrivati ai giorni nostri, con il perfezionamento dei modelli per effettuare, da un lato, previsioni su scala locale ad alto dettaglio spaziale e, dall’altro, per meglio stimare l’incertezza inerente in ogni previsione e aumentarne l’anticipo fino ai limiti teorici stabiliti. Il miglioramento delle reti di monitoraggio meteorologico del nostro pianeta, mediante osservazioni al suolo e in quota, comprese quelle da aerei e da satelliti, hanno costituito il presupposto necessario per rendere attendibili le previsioni globali che si spingono fino a circa una settimana. Allo stesso tempo fenomeni locali intensi, come forti temporali, tornado e alluvioni, iniziano a essere previsti, sia pure a breve termine e con notevoli incertezze, in maniera da permettere allerte utili per prevenire o limitare i danni che da essi possono derivare.
La previsione numerica e l’avvento del calcolo elettronico
Tra il 1916 e il 1922 la strada indicata da Bjerknes venne ripresa dal meteorologo (nonché fisico e matematico) inglese Lewis F. Richardson che, basandosi sulle osservazioni meteorologiche di un particolare giorno sull’Europa, effettuò il primo tentativo di previsione meteorologica mediante uno schema matematico numerico, finalizzato a risolvere le equazioni del moto dell’atmosfera. Le equazioni differenziali, valide per un mezzo continuo, furono convertite da Richardson in un sistema di equazioni algebriche alle differenze finite. Le equazioni algebriche furono ottenute previa definizione di un’opportuna griglia (o maglia) di punti, attribuendo a ogni punto (o nodo) della griglia un numero finito di variabili (pressione, temperatura, velocità e direzione del vento) che rappresentano lo stato medio di una piccola porzione di atmosfera. Il tentativo di Richardson in realtà non ebbe successo per due ragioni. La prima, come fu riconosciuto dallo stesso Richardson, era legata all’insufficiente precisione e copertura spaziale dei dati, specie quelli del vento, allora disponibili. La seconda ragione fu chiarita in seguito, nel 1928, dai matematici Richard Courant, Kurt Friedrichs e Hans Lewy, i quali stabilirono l’esistenza di condizioni piuttosto restrittive che legano il passo temporale Δt, utilizzato per integrare nel tempo le equazioni alle differenze finite, e il passo spaziale Δx, che rappresenta la distanza tra nodi adiacenti della griglia. Soluzioni stabili e realistiche si possono ottenere solo se Δt è inferiore a Δx/V, dove V rappresenta il valore massimo tra la velocità del fluido (che coincide con la velocità del vento nel caso dell’atmosfera) e la velocità di propagazione delle onde all’interno del fluido stesso. Questa è detta condizione CFL, dalle iniziali dei suoi scopritori. Ciò significa che, a parità di V, quanto più piccolo è Δx, ossia quanto migliore è la risoluzione spaziale della griglia, tanto più piccolo deve essere Δt, ossia tanto maggiore deve essere il numero di passi temporali necessari per ottenere la soluzione cercata, per una determinata lunghezza della previsione. Ora, le onde più veloci in atmosfera sono quelle sonore, che viaggiano a circa 330 m/s. Pertanto il passo temporale occorrente per soddisfare la condizione CFL nel caso, per esempio, di Δx=100 km è di soli 5 minuti. Se la condizione CFL non è soddisfatta, si va incontro a un’instabilità dell’algoritmo che compromette la soluzione, come in effetti capitò a Richardson per aver utilizzato passi temporali eccessivamente lunghi. Il numero di operazioni aritmetiche che sarebbero state necessarie a Richardson per effettuare una previsione realistica risulta essere talmente grande che nemmeno il servizio meteorologico numerico da egli stesso immaginato, e che avrebbe dovuto impiegare migliaia di persone addette ai calcoli, avrebbe potuto assolvere allo scopo.
Data la complessità dei calcoli da eseguire, la pre-visione meteorologica numerica non poteva diventare operativa se non dopo l’introduzione del calcolatore elettronico. Nel 1950 i meteorologi Jule G. Charney e Ragnar Fjörtoft e il matematico John Von Neumann produssero il primo tentativo riuscito di previsione con metodi numerici, utilizzando il prototipo di calcolatore elettronico ENIAC (Electronic numerical integrator and computer), sviluppato nel 1946 negli Stati Uniti. Charney aveva elaborato, sulle orme tracciate da Carl-Gustav Rossby nei due decenni precedenti, un sistema di equazioni per descrivere i moti atmosferici, detto quasi-geostrofico. Tale sistema era alquanto semplificato rispetto alle equazioni cosiddette primitive (quelle usate da Richardson) e in grado di eliminare (filtrare) le onde più veloci presenti in atmosfera. L’approssimazione su cui si basa il sistema quasi-geostrofico si fonda sull’ipotesi, valida per i moti a grande scala, che vi sia un quasi equilibrio tra le variazioni della pressione a un livello costante (per es., al livello del mare) e la forza di Coriolis. Il sistema quasi-geostrofico è efficace per una previsione dell’evoluzione della circolazione atmosferica fino a 2÷3 giorni, in quanto è in grado di descrivere gli aspetti fisici che ne dominano l’evoluzione su scale spaziali dell’ordine di 1000 km o più. In questo primo esempio di previsione basata esclusivamente su leggi fisiche veniva calcolata l’evoluzione del campo di geopotenziale al livello della superficie isobarica di 500 hPa (posta all’altezza di ca. 5500 m) sull’emisfero nord. Per associare all’evoluzione di questa variabile una previsione attendibile dei fenomeni meteorologici alla superficie era necessario continuare a fare affidamento su previsori esperti, che potessero interpretare le uscite del modello e correlarle con i parametri da prevedere, sulla base della loro esperienza. In effetti la previsione numerica divenne operativa solamente nel 1954, in Svezia, e l’anno successivo negli Stati Uniti, grazie anche all’accresciuta potenza e affidabilità dei calcolatori.
Per i successivi cinquant’anni di vita della previsione meteorologica numerica, i grandi avanzamenti cui si è assistito hanno beneficiato in misura comparabile sia dei progressi del calcolo sia di quelli della meteorologia dinamica e numerica, senza dimenticare l’apporto altrettanto importante derivato dall’incremento, in densità e precisione, delle osservazioni effettuate ogni giorno su tutto il globo. Il miglioramento dei modelli previsionali negli ultimi decenni è andato di pari passo con il potenziamento dei calcolatori. Alla fine degli anni Sessanta furono gradualmente abbandonate le equazioni filtrate in favore delle equazioni primitive, più accurate per descrivere i moti atmosferici di scala inferiore ai 1000km. Si iniziarono a sperimentare modelli globali, ossia in grado di rappresentare l’evoluzione dell’atmosfera sull’intero globo, mentre nuove tecniche di discretizzazione e soluzione delle equazioni, quali i metodi spettrali o agli elementi finiti, furono introdotte nei modelli stessi.
Al fine di estendere la previsione oltre il periodo di 1-2 giorni delle prime fasi operative, ma anche di aumentarne l’accuratezza, i modelli meteorologici sono stati via via corredati di schemi atti a simulare un numero di processi fisici sempre più elevato, quali: (a) gli scambi turbolenti vicino alla superficie terrestre, nello strato limite atmosferico (SLA); (b) i processi del ciclo dell’acqua e i cambiamenti di stato in atmosfera associati alla formazione delle nubi e delle precipitazioni; (c) la convezione associata alla formazione di nubi cumuliformi e temporali; (d) gli scambi di energia dovuti alla radiazione visibile e infrarossa. Per i processi sopra elencati si parla spesso di parametrizzazioni. Con questo termine si intende una rappresentazione mediante relazioni semplifi-cate di processi fisici che avvengono su scale spazialipiù piccole del passo di griglia, e che quindi non possono essere trattati nello stesso modo esplicito con cui sono trattate le variabili del moto su grande scala. Oltre alle parametrizzazioni dei processi non risolti, i modelli diprevisione meteorologica necessitano del calcolo degli scambi di massa (vapore) e di energia con la superficie, mediante l’accoppiamento dei modelli di atmosfera con modelli di suolo, che comprendono gli effetti della vegetazione, e di oceano.
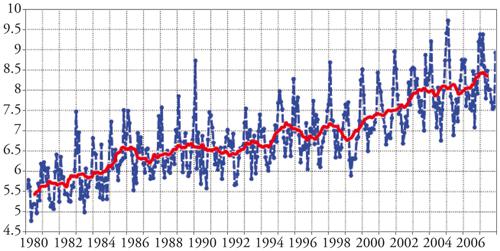
Il relativo successo delle prime previsioni meteorologiche numeriche, basate su modelli emisferici di bassa risoluzione spaziale (passi di griglia superiori ai 500 km e pochi livelli nella verticale), è dovuto al fatto che i moti meteorologici che dominano la circolazione atmosferica e la sua evoluzione a pochi giorni sono essenzialmente di grande scala. La ragione è da ricercare nei vincoli dinamici introdotti dalla rotazione terrestre e dalla stratificazione dell’atmosfera, oltre che nella distribuzione della radiazione solare incidente, che impone un gradiente di temperatura tra l’equatore e i poli. Tuttavia, a causa di processi come l’instabilità convettiva e la deviazione dei flussi da parte delle montagne, una parte dell’energia dei moti atmosferici si ritrova anche su scale di moto piccole e si trasferisce, sia pur lentamente, verso le scale grandi. Per questi motivi, e per ridurre le imprecisioni dovute alle parametrizzazioni, si è cercato di migliorare l’accuratezza delle previsioni aumentando la risoluzione spaziale dei modelli, ossia diminuendone il passo di griglia. Nei modelli globali si è passati da passi di griglia di oltre 500 km agli attuali 25÷30 km, con un centinaio di livelli nella verticale. Considerando sia l’aumento del numero di nodi della griglia sia quello del numero di variabili trattate, si ottiene che gli attuali modelli globali effettuano un numero di operazioni di calcolo che è di circa 100 milioni di volte maggiore di quello dei primi modelli. La potenza di calcolo è nel frattempo passata da circa 1 kiloflop (mille operazioni in virgola mobile al secondo) dell’ENIAC alle decine di teraflop (mille miliardi di operazioni in virgola mobile al secondo) degli attuali supercalcolatori paralleli. Mentre le prime previsioni a 24 ore richiedevano un tempo di esecuzione dell’ordine di una decina di ore (includendo il tempo di acquisizione dei dati), oggi i centri previsionali dotati di supercomputer paralleli, come l’ECMWF, all’incirca nello stesso tempo effettuano una previsione ad alta risoluzione e decine di previsioni a risoluzione inferiore, per un anticipo di 10-15 giorni. L’ECMWF, il più importante centro di meteorologia previsionale in Europa, è stato costituito nel 1973 a Reading (Regno Unito) da diciassette paesi europei, con lo scopo di effettuare previsioni a medio termine, ossia fino a 7-10 giorni. Nel corso dei quasi trent’anni di operatività del centro, si è assistito a un evidente progresso nell’attendibilità della previsione meteorologica. Le previsioni attuali sono in media utilizzabili fino a 7-8 giorni di anticipo, e sono circa equivalenti, come attendibilità, a quelle a 4-5 giorni effettuate all’inizio degli anni Ottanta (fig. 2). È interessante notare che la qualità delle previsioni può variare considerevolmente da un giorno all’altro, specie se si considerano regioni specifiche del globo.
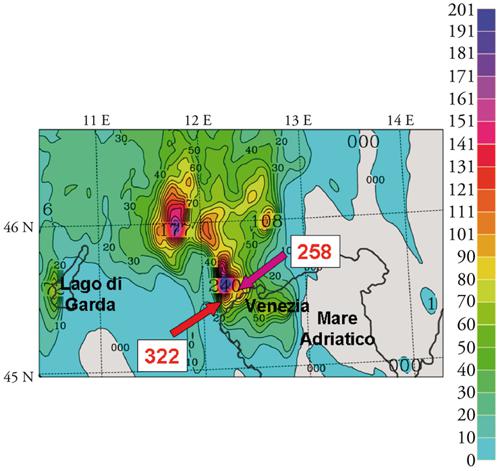
Si è parlato finora principalmente di modelli globali, perché essi sono gli unici che consentono di effettuare previsioni soddisfacenti oltre i 2-3 giorni, a causa delle forti interconnessioni che caratterizzano la circolazione su scala planetaria. Tuttavia, nel caso di previsioni a breve termine (1-3 giorni), per poter aumentare ulteriormente la risoluzione e ottenere quindi un maggiore dettaglio su aree specifiche di interesse, si ricorre ai modelli ad area limitata (LAM, Limited area model). I LAM richiedono che al bordo del volume di atmosfera considerato sia noto l’andamento nel tempo delle variabili atmosferiche, per cui è necessario in ogni caso disporre della previsione di un modello globale. In tal modo si possono effettuare previsioni operative spingendosi fino a un passo di griglia dell’ordine di pochi chilometri (fig. 3). La previsione della precipitazione e di fenomeni legati agli effetti dell’orografia e della superficie (venti orografici, brezze, convezione) beneficiano chiaramente dell’aumento di risoluzione. L’esigenza di migliorare la previsione delle alluvioni, per esempio, che richiede una più precisa quantificazione delle precipitazioni intense, ha stimolato l’utilizzo di modelli ad area limitata da parte di servizi nazionali e regionali. Se ci si vuole spingere a prevedere le precipitazioni su scala regionale oltre le poche ore consentite dai metodi basati sull’estrapolazione delle osservazioni (o nowcasting), i modelli ad alta risoluzione costituiscono l’unico strumento adatto.
I LAM, data l’esigenza di descrivere con maggiore dettaglio i sistemi meteorologici, utilizzano parametrizzazioni differenti e integrano equazioni più complesse di quelle dei modelli globali. Per spingersi a passi di griglia inferiori ai 5÷10 km, è necessario inoltre abbandonare l’approssimazione idrostatica, utilizzata normalmente nei modelli a grande scala, la quale semplifica la relazione che lega la diminuzione della pressione con la quota alla temperatura dell’aria. Si parla quindi di modelli non idrostatici, che, se operanti con risoluzioni di non oltre 2÷3km, permettono anche di risolvere, ossia di descrivere esplicitamente, i fenomeni di convezione organizzata, evitando di ricorrere a parametrizzazioni necessariamente approssimative. A tale scopo i modelli non idrostatici devono essere in grado di descrivere i rapidi processi di condensazione, ghiacciamento e produzione-trasformazione delle diverse forme di precipitazione liquida e solida che avvengono nelle nubi temporalesche, dove si incontrano moti verticali molto intensi. I modelli non idrostatici vengono usati operativamente solo da pochi anni, e tuttora a risoluzioni non del tutto sufficienti a descrivere i fenomeni convettivi. Non si tratta tuttavia solo di affrontare un problema di calcolo, poiché esistono limiti derivanti dalle osservazioni necessarie per definire le condizioni iniziali e limiti di predicibilità intrinseci, particolarmente severi per i fenomeni di piccola scala.
L’assimilazione dei dati meteorologici
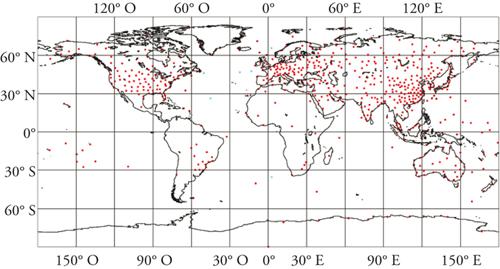
La qualità di una previsione meteorologica a breve e medio termine dipende in maniera essenziale dall’accuratezza con cui è descritto nel modello l’istante iniziale. Ci si basa innanzi tutto sui dati di osservazione che vengono raccolti in continuazione tramite il sistema globale del World Weather Watch, utilizzando reti di misura costituite dalle stazioni al suolo, dalle boe oceanografiche, dai sistemi di radiosondaggio (fig. 4), dagli aerei e dalle navi commerciali, dai radar meteorologici, dai satelliti in orbita polare o geostazionari. Tutti i dati forniti da questi strumenti di osservazione raggiungono rapidamente i centri di previsione numerica, dove vengono elaborati di continuo perché possano concorrere a definire le variabili appropriate sui punti di griglia dei modelli utilizzati per la previsione. La procedura utilizzata a tale scopo è denominata assimilazione dei dati meteorologici nei modelli.
Scopo dell’assimilazione è quello di produrre, a partire dalle osservazioni disponibili che campionano lo stato dell’atmosfera in maniera irregolare nello spazio e nel tempo e che sono affette da errori, una rappresentazione spaziale tridimensionale − o meglio quadridimensionale, considerando anche la dimensione tempo − dello stato dell’atmosfera, che sia il più possibile in accordo con le leggi della dinamica, e in cui l’errore derivante dall’imprecisione dei dati sia, in media, il più piccolo possibile. L’obiettivo è di ottenere uno stato completo dell’atmosfera (detto analisi) a partire da un numero limitato di osservazioni: sono necessarie pertanto informazioni aggiuntive, in genere costituite da un campo di base (background), che rappresenta la miglior stima disponibile a priori dello stato del sistema all’istante considerato. Il campo di background è costituito generalmente da una previsione dallo stesso modello numerico a partire da un istante precedente (per es., sei ore prima). La procedura di assimilazione è sostanzialmente continua nel tempo, o perlomeno viene ripetuta a intervalli frequenti e regolari, propagando in tal modo dinamicamente l’informazione contenuta nelle osservazioni ai tempi precedenti e combinandola con quella che perviene all’istante più recente. Il ciclo previsione-analisi-previsione va visto dunque come un sistema integrato, che deve cercare di minimizzare al contempo gli errori della previsione e dell’analisi.
La previsione probabilisticae di ensemble
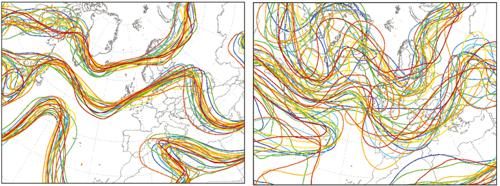
Una volta accertata l’impossibilità di effettuare previsioni deterministiche valide oltre un certo anticipo, si è cercato di rimediare in diversi modi, in particolare utilizzando dei criteri statistici e probabilistici nelle previsioni. Se infatti non possiamo prevedere se, per esempio, fra due giorni vi sarà in una data località una precipitazione di 150 mm su 24 ore, possiamo però tentare di valutare la probabilità che su tale località cada una precipitazione superiore a 100 mm. La semplice climatologia in questo ci aiuta poco, in quanto la frequenza di piogge di questo tipo è, almeno per le nostre regioni, piuttosto bassa. Né in tal caso ci può aiutare il criterio della persistenza, che pure per alcuni parametri (per es., la temperatura) viene considerato come un criterio di confronto (benchmark) da superare. L’unica via praticamente percorribile è quella di tener conto della sensibilità alle condizioni iniziali e alle diverse caratteristiche dei modelli per effettuare un insieme (ensemble, da cui la denominazione del metodo previsionale) che abbiano tutte, a priori, una ragionevole probabilità di verificarsi. A tal fine si introducono variazioni nelle condizioni iniziali, compatibili con l’incertezza con cui si ricavano le osservazioni e le successive analisi, e variazioni nei modelli, compatibili con le incertezze introdotte dagli schemi numerici impiegati, dal tipo e risoluzione delle griglie, dalle parametrizzazioni fisiche. In tal modo si genera un numero elevato di previsioni diversificate, nella speranza di ottenere delle informazioni sull’incertezza reale della previsione a un dato istante (fig. 5). Ritornando all’esempio precedente, si cerca di ricavare una stima della probabilità dell’occorrenza di una precipitazione che superi una certa soglia in un certo intervallo di tempo. A sua volta, la previsione di ensemble è soggetta a molti limiti e fallisce se gli errori dei diversi modelli e delle condizioni iniziali utilizzate non permettono di rappresentare in maniera soddisfacente la reale distribuzione di probabilità del fenomeno da prevedere. Può capitare per esempio che nessuna delle previsioni generate indichi l’occorrenza di precipitazione laddove in realtà pioverà abbondantemente. Quindi la previsione probabilistica, pur essendo in linea di principio più adeguata (e costosa in termini di risorse di calcolo) di quella deterministica per motivi teorici e pratici, è soggetta a sua volta a limitazioni. Certamente è più difficile valutare la bontà di una previsione probabilistica rispetto a una deterministica. Infatti la previsione deterministica vuole rispondere alla domanda: pioverà domani, e se sì, quanto? Facile quindi verificare quanto la previsione sia stata corretta o meno. La previsione probabilistica intende rispondere invece alla domanda: quale è la probabilità che domani cadano più di 5 mm di pioggia? Potremo quindi avere una valutazione precisa della bontà di un certo metodo probabilistico solo dopo aver accumulato un numero molto grande di previsioni di questo tipo e averne valutato le proprietà statistiche.
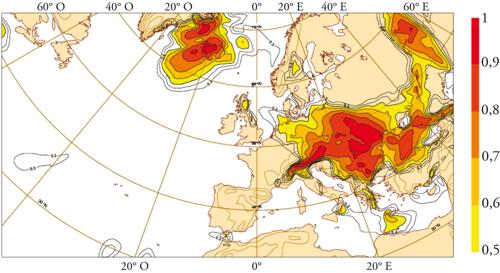
La previsione probabilistica operativa si basa, come si è detto, sulla possibilità di produrre un elevato numero di previsioni distinte variando le condizioni iniziali e i modelli che le generano. La realizzabilità dipende solamente dalle risorse di calcolo disponibili. L’introduzione di supercalcolatori ad architettura parallela ha facilitato questo approccio al problema, nei grandi centri come l’ECMWF si effettuano ogni giorno circa 50 previsioni che costituiscono i membri dell’ensemble. Tali previsioni, dati i limiti computazionali, sono effettuate a risoluzioni spaziali decisamente inferiori a quelle utilizzate per la previsione deterministica. Lo scopo più immediato di queste previsioni di ensemble è quello di fornire indicazioni sulla probabilità di occorrenza di fenomeni estremi o di forte impatto economico e sociale, come tempeste, uragani, piogge alluvionali, nevicate abbondanti (fig. 6). Un altro risultato della previsione probabilistica è definire un indice di attendibilità della previsione deterministica, in funzione di quanto differiscono tra loro i diversi membri dell’ensemble.
Una generazione del tutto casuale di una varietà di condizioni iniziali, al fine di ottenere un ensemble di previsioni, può non essere soddisfacente, per due ragioni, connesse con le proprietà dinamico-statistiche del sistema atmosferico. Innanzi tutto, l’attuale limitazione ad alcune decine di membri dell’ensemble non basta per fornire stime di probabilità accurate. Inoltre, non vi è garanzia che anche un alto numero di condizioni iniziali generate casualmente attorno a un’analisi centrale permetta di ottenere previsioni che realmente consentano di sondare la varietà delle possibili evoluzioni dell’atmosfera in maniera a priori equiprobabile. Per cercare di ovviare a questi problemi, negli ultimi dieci anni sono state introdotte tecniche finalizzate a generare condizioni iniziali che, tenendo conto delle particolari proprietà dinamiche costituite dal modello meteorologico e dal ciclo di assimilazione dei dati, possano fornire ensemble più rappresentativi delle possibili evoluzioni del sistema atmosferico. Esse si basano sull’individuazione, all’istante iniziale o in un suo intorno temporale, dei modi più instabili del sistema modello-assimilazione, ossia quelle strutture spaziali organizzate che tendono a crescere più rapidamente in un certo intervallo di tempo.
Prospettive attuali
Il sistema globale di osservazioni meteorologiche è stato oggetto di notevoli progressi, specie per quanto riguarda i mezzi di telerilevamento, ossia osservazione a distanza, delle proprietà atmosferiche. Sulla scala globale, gli sforzi maggiori sono attualmente concentrati sulle missioni satellitari da parte delle agenzie spaziali, che hanno intensificato negli ultimi anni gli investimenti nel settore delle osservazioni della Terra. Tra la strumentazione a bordo dei satelliti, predominano i sensori passivi, basati sulla rilevazione della radiazione elettromagnetica emessa dalla superficie terrestre, dalle nubi e dall’atmosfera in generale, per i quali si cerca di aumentare in particolare la risoluzione spettrale, ossia la capacità di distinguere le proprietà di frequenze vicine nello spettro della radiazione, utilizzando i metodi dell’interferometria. In questo modo si tende a ridurre gli errori nella valutazione della temperatura superficiale e dei diversi strati dell’atmosfera ricavando informazioni sulla sua composizione, includendo il vapore acqueo, e le nubi. Tutte queste informazioni sono vitali per inizializzare i modelli di previsione meteorologica e i metodi di assimilazione sono ora in grado di utilizzare senza intermediazioni le misure dirette di radiazione fornite dai satelliti.
I satelliti già utilizzano, e lo faranno in misura maggiore nei prossimi anni, anche strumenti attivi, ossia in grado di emettere segnali elettromagnetici e misurarne la componente riflessa dagli strati atmosferici e dalla superficie terrestre. Si tratta di radar e, nel caso in cui si utilizza la banda del visibile o dell’infrarosso, di lidar. Radar a bordo di satelliti sono già utilizzati per ricavare stime dell’altezza e delle proprietà delle onde marine, da cui si possono ottenere informazioni sul vento alla superficie del mare, e per rilevare la presenza di idrometeore nei sistemi che producono precipitazioni. Quest’ultima capacità è decisiva per lo studio della climatologia delle precipitazioni su vaste aree del pianeta scarsamente monitorate, quali in particolare gli oceani e i deserti. La stessa tecnologia consente anche di migliorare la previsione a breve termine con tecniche di assimilazione diretta della precipitazione nei modelli. I lidar a bordo di satelliti sono anche utilizzati per misurare il vapore acqueo e l’aerosol atmosferico, mentre altri metodi di misura della temperatura e dell’umidità atmosferica a livello globale sono basati sull’utilizzo dei segnali GPS (Global positioning system) e sugli effetti di rifrazione che tali segnali subiscono a causa delle variazioni della densità dell’aria.
Contemporaneamente alle osservazioni dallo spazio, si prevede un incremento di quelle da terra, che riguarderanno in particolare la messa in rete di strumenti relativamente costosi, e quindi attualmente non molto diffusi, come i radar meteorologici a doppia polarizzazione (per meglio distinguere le proprietà delle idrometeore) e basati sull’effetto Doppler (per ricavare la velocità del vento), e i profilatori di vento, ossia radar che operano con lunghezze d’onda relativamente grandi e che, puntando verso l’alto, permettono di ricavare la direzione e l’intensità dei moti atmosferici.
Il settore delle osservazioni a mesoscala (la mesoscala in meteorologia comprende l’intervallo di scale di moto tra 1 e 100 km) è finalizzato al miglioramento della previsione a breve e brevissimo termine con un dettaglio spaziale elevato, quale quello richiesto da fenomeni intensi come precipitazioni temporalesche e orografiche, tornado, venti forti associati ai flussi discendenti nei cumulonembi, shear del vento che mette a rischio gli atterraggi degli aerei ecc. È questo forse il campo della previsione su cui si concentrano molti sforzi ma che non produce miglioramenti rapidi. Le limitazioni tecniche attuali risiedono principalmente nella capacità di calcolo e nell’adeguatezza dei dati, ma occorre tener conto dei limiti intrinseci di predicibilità alle piccole scale.
Per quanto riguarda le risorse di calcolo, nonostante gli enormi progressi intervenuti nel settore, non è ancora possibile operare modelli completi con una risoluzione orizzontale inferiore al chilometro e su aree sufficientemente grandi, dell’ordine di 1000×1000 km. Si prevede tuttavia che questo sarà fattibile entro pochi anni. Riguardo all’adeguatezza dei dati, i problemi appaiono di più difficile soluzione data la dimensione degli investimenti necessari. Occorrerebbe infatti disporre di informazioni volumetriche delle principali variabili atmosferiche a elevata risoluzione spaziale (pochi chilometri) e frequenza temporale (dell’ordine delle decine di minuti), con estesa copertura spaziale. Il radar meteorologico è lo strumento che più si avvicina alle caratteristiche richieste, anche se non fornisce tutte le variabili necessarie e la sua precisione è spesso insoddisfacente. Reti integrate di radar meteorologici sono state sviluppate per ora solamente in paesi industrializzati.
Il vincolo forse più stringente all’accuratezza delle previsioni è associato ai limiti di predicibilità dell’atmosfera. Per quanto riguarda le scale relativamente grandi che governano i moti che influenzano la previsione a qualche giorno, gli errori raddoppiano nel corso di un paio di giorni. La causa di questo va ricercata principalmente nell’instabilità baroclina delle medie e alte latitudini. Tuttavia, i fenomeni di piccola scala sono spesso associati a un altro tipo di instabilità atmosferica, quella convettiva. Le nubi che segnalano la presenza di instabilità convettiva sono i cumuli, se l’instabilità è debole, e i cumulonembi (nubi temporalesche), se l’instabilità è forte. I tempi richiesti per la formazione e lo sviluppo di un cumulonembo − dai 15 ai 45 minuti − sono molto più brevi di quelli necessari per formare un ciclone, pari a 1÷2 giorni. Pertanto il tempo di raddoppio degli errori iniziali che comporta la modellistica dei fenomeni di instabilità convettiva è dell’ordine delle decine di minuti. Questo implica un limite di predicibilità al massimo di poche ore. Non possiamo dunque attenderci miglioramenti nella previsione meteorologica a mesoscala analoghi a quelli cui si è assistito negli ultimi anni per le grandi scale. Dato che tuttavia spesso i fenomeni convettivi sono associati all’evoluzione meteorologica a scala più grande, un miglioramento della previsione su tali scale comporta anche un miglioramento nella previsione di tali fenomeni locali (fig. 3).
Ritornando al tema delle osservazioni globali, una delle ricadute della previsione d’ensemble e della determinazione dei modi instabili dell’atmosfera è l’individuazione delle aree cosiddette sensibili. Si tratta delle zone della Terra nelle quali, in un dato istante, gli errori delle osservazioni tendono a crescere più rapidamente. La previsione operativa consente oggi di individuare le aree sensibili giorno per giorno, in funzione della particolare situazione meteorologica. Su questa base di recente si è proposto di effettuare osservazioni mirate su tali regioni, mettendo a punto un sistema di osservazioni adattive, ossia un sistema flessibile che si adatta alla particolare situazione meteorologica. Si tratta di una linea di sviluppo che si affinerà di pari passo con i miglioramenti delle tecniche di analisi e previsione e che promette risparmi sui costi delle osservazioni, migliorandone l’efficienza.
Bibliografia
Buizza 2001: Buizza, Roberto, Chaos and weather prediction. A review of recent advances in numerical weather prediction: ensemble forecasting and adaptive observation targeting,“Il Nuovo Cimento”, 24 C, 2001, pp. 273-301.
Charney 1950: Charney, Jule G. - Fjörtoft, Ragnar - von Neumann, John, Numerical integration of the barotropic vorticity equation, “Tellus”, 2, 1950, pp. 237-254.
Gleick 1987: Gleick, Jack, Chaos, New York, Viking, 1987 (trad. it.: Rizzoli, Milano, 1989).
Holton 1992: Holton, James R., An introduction to dynamic meteorology, 3. ed., San Diego, Academic Press, 1992.
Kalnay 2002: Kalnay, Eugenia, Atmospheric modeling, dataassimilation and predictability, Cambridge, CambridgeUniversity Press, 2002.
Lorenz 1963: Lorenz, Edward N., Deterministic nonperiodic flow, "Journal of atmospheric science”, 20, 1963, pp. 130-141.
Lorenz 1993: Lorenz, Edward N., The essence of chaos, London, UCL, 1993.
Navarra 1996: Navarra, Antonio, Le previsioni del tempo,Milano, Il Saggiatore, 1996.
Palmer 2000: Palmer, Tim N., Predicting uncertainty in forecasts of weather and climate, “Reports on progress in physics”, 63, 2000, pp. 71-116.
Palmer, Hagedorn 2006: Predictability of weather and climate, edited by Tim N. Palmer, Renate Hagedorn, Cambridge, Cambridge University Press, 2006.
Palmieri 2000: Palmieri, Sabino, Il mistero del tempo e delclima, Napoli, Cuen, 2000.
Tavola I
edward lorenz: atmosfera e caos
Verso la fine degli anni Cinquanta del Novecento, Edward Lorenz, professore di meteorologia al MIT (Massachusetts Institute of Technology) di Boston, si stava interessando del problema della previsione meteorologica basata su metodi puramente statistici. In quel periodo infatti si riteneva che il metodo statistico, basato sull’utilizzo di relazioni empiriche tra l’evoluzione delle variabili meteorologiche, potesse competere sia con il metodo sinottico tradizionale sia con i modelli numerici, che stavano dando risultati ancora insoddisfacenti. Poiché tuttavia non si disponeva di serie di dati meteorologici sufficientemente lunghe, Lorenz inventò un modello matematico alquanto semplificato della circolazione atmosferica, basato su dodici equazioni e altrettante variabili. Con tale modello egli poteva produrre lunghe serie temporali di dati simulati, sui quali mettere alla prova il metodo statistico. Per certi valori dei parametri il modello produceva stati stazionari o periodici nel tempo, per i quali il metodo di previsione statistico funzionava fin troppo bene, ma che evidentemente non rappresentavano la complessità dell’atmosfera reale. Lorenz notò tuttavia che, per altri valori di quei parametri, emergevano soluzioni dalle proprietà inaspettate, non periodiche nel tempo, ossia irregolari, e il cui andamento nel tempo non era prevedibile con il metodo statistico. Egli comprese che questo secondo tipo di soluzioni erano quelle che meglio rappresentavano il comportamento in gran parte non periodico della circolazione atmosferica. Ma la proprietà che lo colpì di più era la grande sensibilità alle condizioni iniziali: per quanto numericamente vicini fossero scelti due stati iniziali, inevitabilmente, nel caso di soluzioni irregolari, essi conducevano in breve a stati del sistema molto diversi tra loro. Come dire che due situazioni meteorologiche molto simili tra loro non portano a evoluzioni successive altrettanto simili, per cui la previsione del tempo basata sugli analoghi non funziona in maniera soddisfacente. Lorenz poco più tardi, durante un congresso a Tokio del 1960, dimostrò la stretta relazione esistente tra la sensibilità alle condizioni iniziali e il comportamento caotico.
Tre anni dopo, Lorenz pubblicò un altro lavoro fondamentale basato su un modello di sistema dinamico ancora più semplice, costituito da sole tre equazioni e tre incognite. Tale modello descriveva, in maniera idealizzata, il moto convettivo di un fluido riscaldato dal basso. Anche questo sistema, soggetto a forzatura e dissipazione (ossia a effetti di attrito), presentava un comportamento caotico e sensibilità alle condizioni iniziali, nonostante il numero di variabili (gradi di libertà) fosse estremamente ridotto (tre è in effetti il numero minimo di gradi di libertà che consente un comportamento caotico, come nel caso del problema dei tre corpi di Poincaré). La scoperta si rivelò essere di portata molto generale, con ricadute che si estendevano ben oltre il campo della meteorologia: si comprendeva che il caos non è necessariamente dovuto, come comunemente si riteneva fino ad allora, a effetti casuali (stocastici) associati all’esistenza di un grandissimo numero gradi di libertà, come nel caso del moto molecolare in un gas. Il comportamento caotico di un sistema deterministico (detto caos deterministico) è in effetti una proprietà intrinseca alla dinamica del sistema ed è strettamente associata alla sensibilità alle condizioni di partenza. Quest’ultima proprietà è a sua volta legata al concetto di impredicibilità: non possiamo prevedere con esattezza, e oltre un certo intervallo di tempo, il comportamento di un sistema caotico, dal momento che non ne possiamo conoscere con precisione infinita lo stato a un determinato istante, che definiamo come istante iniziale. Il limite nella predicibilità dipende dal fatto che errori nella definizione della condizione iniziale tendono a crescere tanto più rapidamente quanto più essi sono piccoli, per cui un miglioramento nella precisione della conoscenza dello stato iniziale non comporta un aumento proporzionale nell’accuratezza della previsione. Questo limite nella predicibilità di un sistema caotico vale anche per la previsione meteorologica.
La teoria del caos deterministico, come paradigma universale di moltissimi fenomeni anche molto lontani dalla meteorologia, nonché la teoria dei sistemi dinamici e dei frattali, ha ricevuto un grande impulso a partire dagli anni Settanta del secolo passato. Quello che spesso è poco noto è il ruolo giocato dal problema della previsione del tempo nel dare inizio a questo nuovo ramo della fisica e della matematica, con applicazioni che vanno dalla chimica all’ingegneria, dalla biologia alla medicina, dall’economia all’informatica e così via. È soltanto con lo sviluppo di questi strumenti concettuali che si è potuta dare una risposta scientifica rigorosa, anche se ancora incompleta, all’antico interrogativo: perché gli astri seguono (solitamente) leggi precise, che consentono la previsione delle loro orbite anche con secoli di anticipo, mentre non siamo in grado di prevedere a volte con nemmeno poche ore di anticipo i fenomeni dell’atmosfera? La risposta è venuta dalla scoperta delle proprietà dei sistemi dinamici. Il risvolto più sorprendente è che le differenze profonde non sono da ricercarsi tanto nella complessità degli elementi costitutivi dei due diversi sistemi, quanto nelle differenti proprietà matematiche delle leggi che ne regolano l’evoluzione.
I progressi della previsione meteorologica negli ultimi trent’anni, per quelli che sono gli aspetti non direttamente connessi con lo sviluppo dei modelli e dei sistemi osservativi, sono venuti in buona parte a seguito delle ricerche di Lorenz tra gli anni Sessanta e gli anni Novanta. Nel 1972 egli presentò quello che divenne un famoso principio dagli aspetti paradossali, con il titolo: Predicibilità: possono i battiti delle ali di una farfalla in Brasile scatenare un tornado nel Texas? Nella trattazione che seguiva, Lorenz non dava una risposta perentoria: così come certe perturbazioni molto piccole possono effettivamente cambiare l’evoluzione dell’atmosfera, altre possono non avere alcun effetto, e comunque non cambiano il clima, ossia la frequenza con cui i fenomeni meteorologici si manifestano. Che tuttavia l’atmosfera sia, in molte circostanze, instabile e quindi sensibile a perturbazioni infinitesime lo si può sperimentare mediante un modello numerico di circolazione globale: se si altera per esempio la temperatura anche in un solo punto di griglia e solamente di un centesimo di grado, dopo circa dieci-quindici giorni di simulazione, confrontando due esperimenti gemelli, quello perturbato con quello non perturbato, si osserveranno differenze di molti gradi, su regioni anche molto lontane da quella dove è stata introdotta la perturbazione.
Un altro contributo dovuto principalmente a Lorenz, nel corso degli anni Ottanta, è consistito nel definire i limiti di predicibilità dell’atmosfera, distinguendo la previsione deterministica delle variabili a un singolo istante e per una singola località dalla previsione di valori medi nel tempo e nello spazio, in termini di deviazioni rispetto all’andamento climatologico. La previsione meteorologica riguarda la prima modalità. In tal caso, il limite massimo non sembra poter eccedere i 15-20 giorni. Nonostante i recenti progressi, i limiti pratici attuali di previsione si collocano a circa la metà o poco più di tale valore. Essi sono dovuti, all’incirca in ugual misura, sia agli errori nei dati di osservazione sia ai difetti insiti nei modelli.