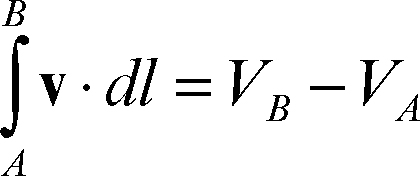vettore, potenziale di un

Enciclopedia della Matematica (2013)

vettore, potenziale di un


vettore, potenziale di un funzione ƒ: R3 → R le cui derivate rispetto agli assi coordinati sono le componenti del vettore v. Si ha perciò

formula

dove i, j, k sono i versori degli assi. Tale funzione, tradizionalmente indicata anche con V, esiste quando l’integrale di v lungo ogni linea chiusa è nullo. In tale caso, l’integrale di linea del vettore v tra due punti A e B, non dipende dalla particolare linea che collega i due punti e si ha

formula

dove l’operazione indicata è il prodotto scalare. I campi che ammettono potenziale sono tra i più importanti della fisica (per esempio: campo gravitazionale, campo elettrostatico ecc.) e sono detti campi conservativi perché per essi vale il principio di conservazione dell’energia.

Si dimostra che un campo conservativo è necessariamente irrotazionale, cioè rotv = 0, e vale il viceversa se il dominio in cui il campo è definito è semplicemente connesso.

Vedi anche
gradiente La variazione per unità di lunghezza che una grandezza subisce da un punto all’altro dello spazio lungo una certa direzione. In analisi vettoriale, data una funzione scalare del posto, U (x, y, z), regolare, si chiama g. di U il vettore v=gradU, di componenti cartesiane La funzione U si chiama potenziale ... forza viva In fisica, lo stesso che energia cinetica (➔ energia). Teorema delle forze v. Deduzione dai principi della dinamica secondo la quale in un sistema meccanico la variazione di energia cinetica è uguale al lavoro meccanico effettuato da, o sul, sistema stesso. onda Con riferimento a un dato mezzo fisico (acqua, aria ecc.), perturbazione determinatasi in un punto del mezzo che si propaga nello spazio trasportando energia ma non materia. Fisica Propagazione per onde Si parla di propagazione per o. di una perturbazione tutte le volte che in uno o più punti di un ... superconduzione In fisica, particolare tipo di conduzione, detto anche superconduttività, che alcuni elementi, alcuni composti e alcune leghe presentano nei riguardi della corrente elettrica. Il fenomeno fu scoperto nel 1911 da H. Kamerlingh Onnes nel mercurio e, in breve tempo, confermato in varie altre sostanze. Caratteri ...
Tag
Altri risultati per vettore, potenziale di un
  • potenziale
    Enciclopedia on line
    In fisica, funzione introdotta per caratterizzare particolari campi di forza posizionali ed estesa, sotto opportune condizioni, a campi vettoriali di natura qualsiasi. Per estensione, il complesso dei mezzi, delle capacità, delle risorse ecc. di cui si dispone o si può disporre per il conseguimento ...
  • potenziale
    Dizionario delle Scienze Fisiche (1996)
    potenziale [agg. e s.m. Der. del lat. potentialis, da potentia "potenza"] [LSF] (a) In contrapp. ad attuale, di ciò che ha la capacità di esplicarsi in qualcosa, ma non attuandosi ancora. (b) Funzione, inizialmente introdotta per esprimere l'energia p. (nel signif. precedente) di un oggetto in un campo ...
Vocabolario
potenziale
potenziale agg. e s. m. [dal lat. tardo potentialis, der. di potentia «potenza»]. – 1. agg. a. Nel linguaggio filos., che concerne la potenza, che è in potenza (nel senso partic. per cui potenza si contrappone ad atto): intelletto p., che...
vettóre
vettore vettóre s. m. [dal lat. vector -oris «conducente, portatore», der. di vehĕre «condurre, portare», part. pass. vectus]. – 1. Nel contratto di trasporto, colui che si obbliga, verso corrispettivo, a trasferire persone o cose da un...