ponti di Konigsberg, problema dei

ponti di Konigsberg, problema dei

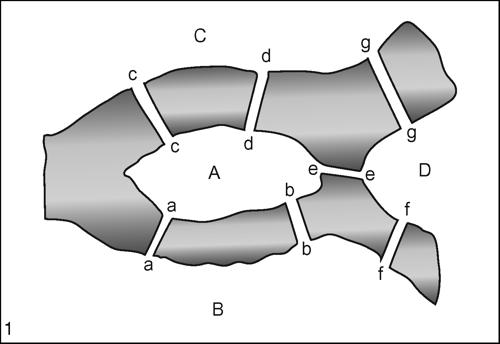
ponti di Königsberg, problema dei storico problema che la tradizione vuole legato alla città di Königsberg della Prussia orientale (oggi Kaliningrad, in Russia), nota per aver dato i natali a Immanuel Kant (1724-1804). Il problema riguarda la possibilità di compiere un percorso (cammino semplice) attraversando tutti i ponti della città e passando per ognuno di essi una (e una sola) volta. Alla semplicità dell’enunciato, nei termini in cui la tradizione vuole fosse posto dagli abitanti del luogo, non corrisponde un’altrettanto semplice soluzione matematica della questione. In termini moderni, il problema si risolve attraverso le proprietà di percorribilità di un → grafo, ma utilizzando prove empiriche, la maggior parte delle persone di quel tempo sembra propendesse per una risposta negativa. Fu Eulero a fornire la dimostrazione generale del problema nel trattato Solutio problematis ad geometriam situs pertinentis del 1741; nella sua soluzione si individua oggi l’origine della moderna teoria dei grafi: «Dato dunque un qualunque caso, si può immediatamente e molto facilmente riconoscere se la passeggiata, alle note condizioni, è possibile o meno, a causa della seguente regola: se le regioni alle quali conducono un numero dispari di ponti sono più di due, allora si può affermare con certezza che la passeggiata è impossibile. Se le regioni alle quale conducono un numero dispari di ponti sono solo due, allora la passeggiata è possibile, a patto che si parta da una di esse. Se infine un numero dispari di ponti non giunge ad alcuna regione, allora la passeggiata è possibile, qualunque sia la regione dalla quale si parte. E questa regola è del tutto sufficiente, qualunque siano le condizioni del problema posto». Eulero stabilì quindi le seguenti generalizzazioni:

• soltanto un grafo composto da nodi collegati da un numero pari di archi (nodi di ordine pari), può essere percorso toccando una e una sola volta tutti i nodi in modo da ritornare infine al punto di partenza; in pratica si effettua un percorso che è un → ciclo euleriano;

• se il grafo contiene nodi di ordine pari ma soltanto due nodi collegati con un numero dispari di archi (nodi di ordine dispari) esso è ancora percorribile, ma occorre partire da uno dei due nodi dispari ed arrivare all’altro nodo dispari; in questo caso non è quindi possibile giungere alla fine del percorso allo stesso nodo di partenza;

• se il grafo contiene più di due nodi di ordine dispari esso non è più definibile come ciclo euleriano, in quanto risulta impossibile percorrerlo senza dover attraversare archi già toccati in precedenza.

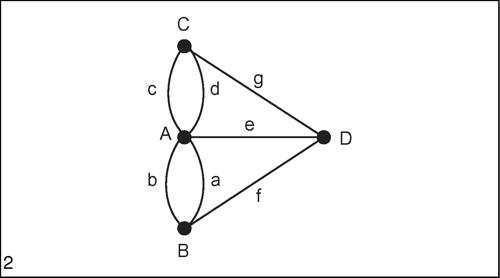
Analizzando il problema dei ponti di Königsberg con il formalismo dei grafi, il percorso può essere rappresentato con un grafo con 4 nodi, A, B, C, D collegati da 7 archi e aventi tutti ordine dispari, rispettivamente ordine 5, 3, 3, 3. Il problema, quindi, non ammette soluzione.