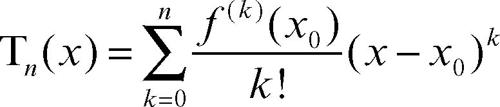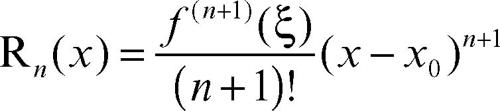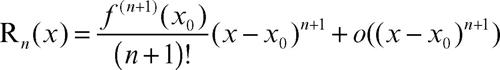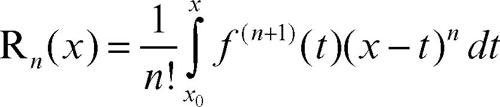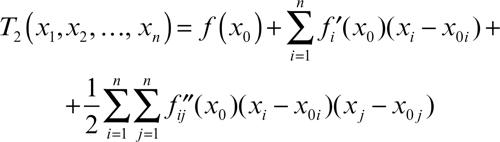Taylor, polinomio di
Taylor, polinomio di
Taylor, polinomio di (di grado n) per una funzione ƒ(x) dotata delle derivate fino all’ordine n-esimo in un punto x0 è il polinomio
che in x0 ha lo stesso valore di ƒ(x) e le stesse derivate fino all’ordine n.
Fra tutti i polinomi di grado non superiore a n, il polinomio di Taylor è quello che meglio approssima asintoticamente ƒ(x), nel senso che è l’unico il cui errore è o((x − x0)n) per x → x0 (si veda → o piccolo). Nel caso in cui x0 = 0, si parla più precisamente di polinomio di → Maclaurin.
La formula di Taylor ƒ(x) = Tn(x) + Rn(x) mostra che ƒ(x) si può sostituire con il suo polinomio di Taylor a meno di un resto Rn(x), detto resto della formula di Taylor o anche resto del polinomio di Taylor. Il resto assume diverse forme, di cui le più importanti sono quelle:
• di → Lagrange
• di → Peano
• e il resto integrale
valido se ƒ ammette derivata continua in [x0, x].
Se, al tendere di n all’infinito, il resto Rn tende a zero, si ha la serie di Taylor (→ Taylor, serie di).
Un’altra scrittura equivalente della formula di Taylor è:
che sinteticamente si può scrivere, usando i differenziali successivi, come
Quest’ultima espressione si generalizza a più variabili, usando l’espressione dei differenziali per tali funzioni. Per esempio, il polinomio di secondo grado relativo al punto x0 = (x01, x02, …, x0n) ha la forma:
