poligono
poligono
Le figure più elementari nelle due dimensioni
I poligoni, regolari o no, sono le figure di base della geometria del piano e la loro classificazione aiuta a capirne le proprietà. Triangoli e quadrilateri, pentagoni, esagoni e via dicendo, con le loro forme armoniose e compatte, hanno incuriosito i matematici e ispirato gli architetti
Poligoni e palazzi
Nella maggior parte dei casi la pianta di un edificio è formata da uno o più rettangoli uniti, ma esistono alcune eccezioni, come per esempio il Pentagono, il quartier generale del dipartimento statunitense della Difesa. Un altro edificio non rettangolare, nato per esigenze militari, è Castel del Monte, in provincia di Bari, a pianta ottagonale, fatto costruire a metà del 13° secolo dall’imperatore Federico II di Svevia.
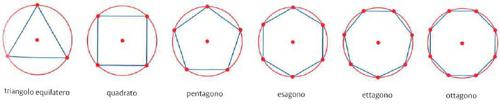
Il pentagono e l’ottagono usati come piante di questi edifici sono esempi di poligoni regolari, cioè di poligoni con tutti i lati e tutti gli angoli uguali. I poligoni regolari ricevono un nome particolare a seconda del numero di lati e, via via che esso aumenta, sempre più si avvicinano al cerchio, nel quale possono essere inscritti (v. fig.). I poligoni regolari fanno parte di una classe più ampia di figure piane, chiamate semplicemente poligoni. Disegniamo più segmenti, l’uno dopo l’altro; si ottiene così una linea spezzata.
Se la linea spezzata si chiude senza che i segmenti si intersechino tra loro, abbiamo ottenuto un poligono.
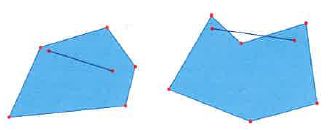
Possiamo così definire un poligono come una figura piana delimitata da segmenti (i suoi lati); esso divide il piano in due parti: la zona interna e quella esterna al poligono stesso. I poligoni che più interessano sono quelli convessi, che cioè non presentano ‘rientranze’. Più precisamente, un poligono è convesso quando, presi due punti qualsiasi al suo interno, il segmento che li unisce è tutto interno al poligono stesso (v. fig.).
Triangoli
I triangoli sono i poligoni con il minor numero di lati. Essi hanno una proprietà, molto importante per l’ingegneria e l’architettura: sono indeformabili perché la lunghezza dei lati determina l’ampiezza degli angoli (una deformazione implica sempre una variazione di ampiezza degli angoli). Gli altri poligoni, con lati di uguali misure, possono, invece, assumere diverse forme.
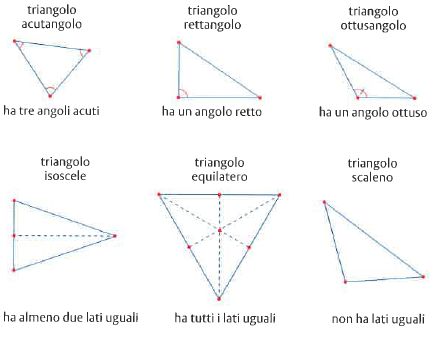
I triangoli si classificano in base agli angoli oppure ai lati (v. fig.). In base agli angoli si distinguono tre tipi di triangoli: acutangolo, rettangolo, ottusangolo.
Un triangolo non può avere più di un angolo ottuso (cioè di ampiezza maggiore di 90°) perché la somma dei suoi angoli equivale a un angolo piatto (la cui ampiezza è 180°).
In base ai lati si distinguono tre tipi di triangoli: isoscele, equilatero e scaleno. Il triangolo isoscele è simmetrico rispetto a un asse, mentre il triangolo equilatero è simmetrico rispetto a tre assi.
Quadrilateri
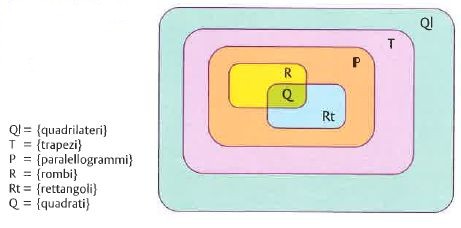
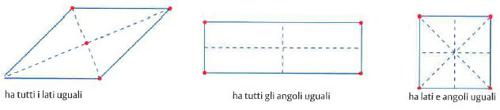
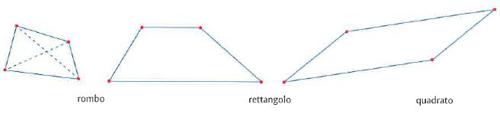
I quadrilateri sono i poligoni con quattro lati (v. fig.). Se due lati sono paralleli, il quadrilatero si chiama trapezio. Se sono paralleli anche gli altri due lati, il quadrilatero si chiama parallelogramma. I parallelogrammi, a loro volta, sono classificati in base all’uguaglianza di lati o angoli (v. fig.).
Si può osservare che il rombo è simmetrico rispetto alle sue diagonali, mentre il rettangolo è simmetrico rispetto alle linee che congiungono i punti medi dei lati opposti. Il quadrato ha tutte le proprietà sia del rombo (ha tutti i lati uguali ed è simmetrico rispetto alle diagonali) sia del rettangolo (ha tutti gli angoli uguali e retti ed è simmetrico rispetto alle linee mediane dei lati). Il quadrato è perciò un rombo che è anche rettangolo (v. fig.).