Reuleaux, poligoni di
Reuleaux, poligoni di
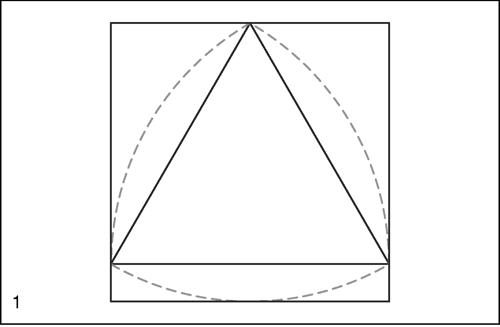
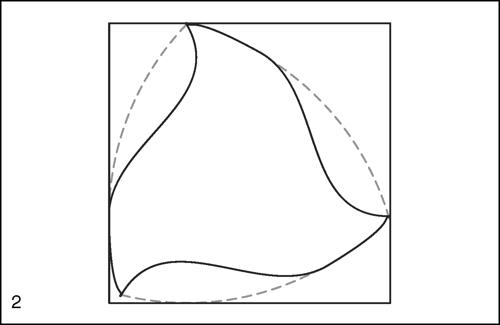
Reuleaux, poligoni di figure piane, ottenute a partire da poligoni convessi con un numero dispari di vertici, che hanno la caratteristica di essere curve con ampiezza costante. Una curva chiusa ha ampiezza costante quando, dato un punto qualunque della curva e considerata la sua distanza massima dagli altri suoi punti, tale distanza è indipendente dal punto scelto. Esempio banale di curva con ampiezza costante è la circonferenza (il diametro ha ampiezza 2r). La più semplice di tali figure, diversa dalla circonferenza, è il cosiddetto triangolo di Reuleaux, ottenuto a partire dal triangolo equilatero. Il nome è dovuto all’ingegnere meccanico Franz Reuleaux (1829-1905), docente a Zurigo e Berlino e autore di importanti contributi nel campo della storia della tecnica e delle costruzioni di macchine. Il triangolo di Reuleaux si ottiene tracciando da ogni vertice del triangolo un arco di circonferenza avente per raggio il lato del triangolo e per estremi i vertici opposti. La sua ampiezza costante è il lato d del triangolo. Il triangolo di Reuleaux ha la proprietà di essere inscrivibile in un quadrato di lato d e, ruotandolo comunque attorno al centro, è sempre tangente internamente al quadrato stesso. Per tale proprietà esso trova varie applicazioni. Per esempio, opportunamente sagomato, esso può fare da punta di un trapano per realizzare fori quadrati; anche i plettri per chitarra hanno la forma di un triangolo di Reuleaux. In modo analogo, a partire da un qualunque poligono regolare con un numero dispari di vertici, si costruiscono i poligoni di Reuleaux con 2n + 1 vertici, la cui ampiezza costante d è data dalla lunghezza delle 2n + 1 diagonali di lunghezza massima. È possibile costruire poligoni di Reuleaux anche a partire da poligoni convessi non regolari con un numero dispari di vertici purché le diagonali che uniscono ogni vertice ai vertici del lato opposto abbiano la stessa lunghezza. Il contorno di una curva con ampiezza costante d è πd (→ Barbier, teorema di).