podaria
podaria
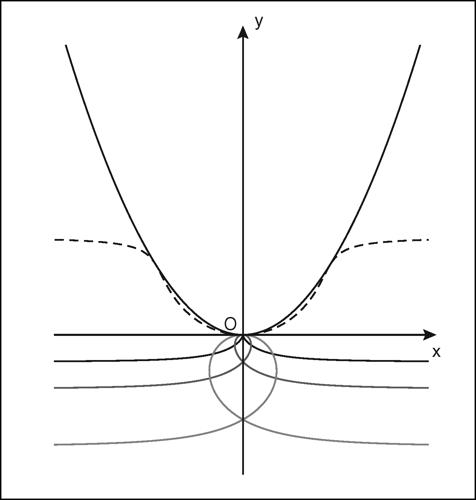
podaria in geometria, la podaria o pedale di una curva piana γ rispetto a un punto P è il luogo dei punti del piano formato dalle proiezioni di P sulle rette tangenti alla curva, cioè il luogo dei piedi delle perpendicolari condotte da P alle tangenti alla curva. Il punto P è detto polo e la curva γ antipodaria o podaria negativa o antipedale e può essere considerata come l’inviluppo delle perpendicolari condotte alle rette uscenti da P nei loro punti di intersezione con la curva data. La podaria di una circonferenza è una lumaca di → Pascal. La podaria di una parabola può assumere diverse configurazioni a seconda della posizione del polo; in particolare può risultare:
• una retta (la sua tangente nel vertice), se il polo è il fuoco della parabola;
• una → cissoide, se il polo è il vertice della parabola;
• una → trisettrice di Maclaurin, se il polo è il simmetrico del fuoco rispetto alla direttrice della parabola.
La podaria di un’ellisse rispetto a un suo fuoco è una circonferenza, con centro nel centro dell’ellisse e raggio uguale al diametro maggiore dell’ellisse. La podaria di un’iperbole rispetto a un suo fuoco è una circonferenza, con centro nel centro dell’iperbole e tangente a essa, mentre se il polo è il centro dell’iperbole la podaria è una → lemniscata con gli stessi assi di simmetria dell’iperbole.
Analogamente nello spazio si dice podaria o pedale di un punto rispetto a una superficie il luogo dei piedi delle perpendicolari condotte dal punto a tutti i piani tangenti alla superficie data.
Particolari podarie, secondo una classificazione che si basa sulla loro equazione, sono: a) (del terzo ordine) la → concoide di Sluse, l’→ ofiuride, la → cissoide di Diocle; b) (del quarto ordine) la lumaca di → Pascal, la lemniscata di → Booth; c) (del sesto ordine) lo → scarabeo.