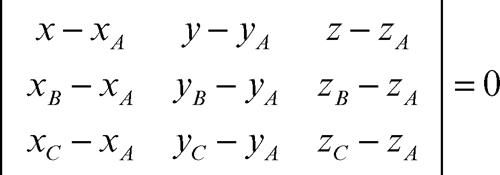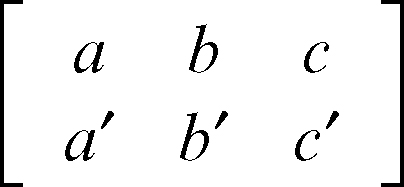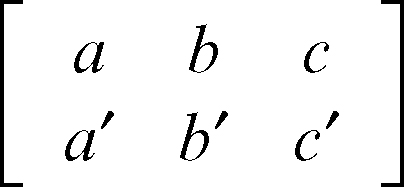piano

piano

piano concetto primitivo della geometria la cui natura è di volta in volta precisata mediante l’introduzione di opportuni sistemi di assiomi che collegano questa nozione alle altre nozioni fondamentali di punto, retta e spazio. Il termine è usato anche per denotare particolari insiemi dotati di struttura algebrica (→ piano affine reale; → piano vettoriale su un campo K; → piano proiettivo; → spazio proiettivo di dimensione 2).

Nella geometria euclidea è implicitamente definito attraverso gli assiomi (→ geometria euclidea; → definizione). Nell’ordinario spazio euclideo tridimensionale un piano è individuato da tre suoi punti non allineati (per tre punti che non appartengono alla stessa retta passa uno e un solo piano) oppure da una retta e un punto esterno a essa. Due piani possono essere paralleli o incidenti. Nel primo caso sono privi di punti comuni, oppure hanno tutti i punti in comune (coincidono). Nel secondo caso hanno una retta in comune. Due piani incidenti, in particolare, risultano perpendicolari se formano quattro diedri uguali. Un piano è detto punteggiato se lo si considera come un insieme di punti; è detto rigato se lo si considera come un insieme infinito di rette (per le accezioni del termine piano in geometria proiettiva si veda il lemma → forma). Se lo spazio è dotato di un sistema di riferimento Oxyz, l’equazione di un piano è del tipo ax + by + cz + d = 0, con a, b, c non tutti nulli. Dal punto di vista vettoriale un piano può essere assegnato come combinazione lineare di due vettori linearmente indipendenti applicati in uno stesso punto. Il piano individuato dai vettori linearmente indipendenti u e v, passante per il punto P₀, ha equazione vettoriale

L’equazione di un piano passante per tre punti distinti A(x_A, y_A, z_A), B(x_B, y_B, _,z_B), C(x_C, y_C, z_C) è invece

Una ulteriore rappresentazione di un piano si ha mediante un’equazione del tipo

detta equazione segmentaria, nella quale i coefficienti p, q, r, indicano, rispettivamente, le coordinate non nulle delle intersezioni del piano con l’asse x, con l’asse y, con l’asse z. A ogni piano di equazione ax + by + cz + d = 0 è associato il vettore giacitura (a, b, c) a esso perpendicolare. Questa proprietà permette di stabilire la posizione reciproca di due piani esaminando i rispettivi vettori giacitura. In particolare, dati due piani di rispettive equazioni ax + by + cx + d = 0 e a′x + b′y + c′z + d′ = 0, essi risultano:

• paralleli se e solo se i rispettivi vettori giacitura sono linearmente dipendenti (paralleli), cioè se la matrice

ha rango minore di 2;

• incidenti se e solo se i rispettivi vettori giacitura sono linearmente indipendenti (non paralleli), cioè se la matrice

ha rango 2. In particolare, i due piani sono perpendicolari se è nullo il prodotto scalare delle giaciture, cioè se risulta aa′ + bb′ + cc′ = 0.

In geometria differenziale il piano è una superficie avente entrambe le curvature fondamentali nulle (si veda anche → distanza di un punto da un piano; → distanza tra due piani paralleli).