Galilei, paradosso di
Galilei, paradosso di
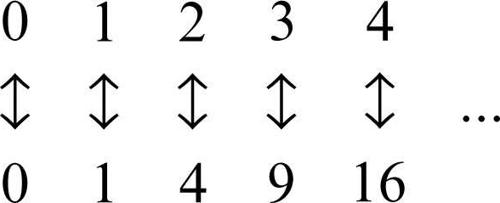
Galilei, paradosso di o paradosso dell’infinito, paradosso che consiste nella possibilità di porre in corrispondenza biunivoca un insieme infinito con un suo sottoinsieme proprio. Galileo osservò nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638) che è possibile stabilire una corrispondenza biunivoca tra l’insieme dei numeri naturali (escludendo 0) 1, 2, 3, 4, ... e l’insieme dei quadrati perfetti 1, 4, 9, 16, ... associando a ogni numero naturale il suo quadrato e, viceversa, a ogni quadrato perfetto la sua radice quadrata non negativa; la corrispondenza può essere completata associando a 0 sé stesso. Si ha, quindi, lo schema seguente:
L’insieme dei numeri naturali è così in corrispondenza biunivoca con una sua parte propria, cioè con un suo sottoinsieme proprio. Ciò appare paradossale se si considera il principio che «il tutto è sempre maggiore della parte». Tuttavia, questo principio è valido per gli insiemi finiti mentre per gli insiemi infiniti, come l’insieme dei naturali, esiste la possibilità di avere tanti elementi quanti sono quelli di un proprio sottoinsieme. Questa caratteristica è stata assunta da R. Dedekind (1888) proprio per definire che cosa si intenda per insieme infinito o, più precisamente, per infinità attuale di un insieme: «un insieme è infinito quando e soltanto quando può essere posto in corrispondenza biunivoca con una sua parte propria».