Bertrand, paradosso di
Bertrand, paradosso di
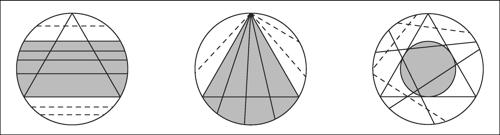
Bertrand, paradosso di problema di probabilità geometrica, la cui paradossalità consiste nell’avere differenti soluzioni a seconda del metodo di selezione casuale scelto. Il problema, posto da J.-L.-F. Bertrand nel 1888, consiste in questo: dato un triangolo equilatero inscritto in un cerchio, calcolare la probabilità che una corda del cerchio, scelta a caso, abbia lunghezza maggiore del lato del triangolo. Si esaminino diversi metodi di scelte a caso:
a) primo metodo di selezione casuale: si considerano tutte le corde parallele a un lato del triangolo; di queste sono più lunghe del lato del triangolo solo quelle che distano dal centro meno della metà del raggio. La probabilità cercata è perciò 1/2;
b) secondo metodo di selezione casuale: scelto un punto sulla circonferenza, si considerano tutte le corde del cerchio che hanno tale punto come estremo; di queste solo quelle parzialmente interne al triangolo che ha un vertice nel punto scelto sono più lunghe del lato. Tali corde hanno l’altro estremo su un arco che è 1/3 della circonferenza. La probabilità cercata è perciò 1/3;
c) terzo metodo di selezione casuale: scelto un punto qualunque del cerchio, si considerano le corde che hanno esso come punto medio; di tali corde sono maggiori del lato del triangolo solo quelle il cui punto medio cade nel cerchio inscritto al triangolo. Poiché l’area di tale cerchio è 1/4 di quella del cerchio circoscritto, la probabilità cercata è 1/4.
Le tre differenti soluzioni dipendono dall’indeterminatezza dell’espressione «scelta a caso», che, non specificando la particolare procedura di scelta, dà luogo a tre problemi differenti a seconda dell’interpretazione che se ne voglia dare.