paraboloide
paraboloide
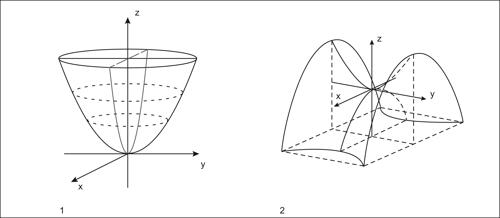
paraboloide quadrica non degenere e tangente al piano all’infinito. Il paraboloide è privo di centro di simmetria, ma è dotato in generale di due piani di simmetria ortogonali (piani principali) che si segano secondo una retta (che è un asse di simmetria) la cui intersezione propria col paraboloide è il suo vertice. In un riferimento cartesiano l’equazione canonica del paraboloide ha una delle sue seguenti forme:
a seconda che si tratti rispettivamente di paraboloide ellittico, detto così perché la sua intersezione con un piano di equazione z = k è un’ellisse, o di paraboloide iperbolico, così detto perché la sua generica intersezione con un piano di equazione z = k è un’iperbole; quest’ultimo è detto anche paraboloide a sella perché il suo vertice è un punto di sella. Nel primo caso la superficie è rotonda quando a = b, e può essere ottenuta facendo ruotare una parabola intorno al proprio asse. Il paraboloide ellittico è allora detto paraboloide circolare o paraboloide di rivoluzione.
Il paraboloide iperbolico può essere generato da una parabola che si muove mantenendosi parallela al suo piano in modo che il suo vertice sia vincolato su una seconda parabola fissa, posta su un piano perpendicolare a quello della prima parabola, ma con concavità nel verso opposto. Il paraboloide iperbolico è una superficie rigata formata da tutte le rette parallele a un dato piano che si appoggiano su due date rette sghembe; in particolare, è una quadrica doppiamente rigata perché per ogni suo punto passano due rette interamente appartenenti alla superficie. Le rette del paraboloide sono raggruppate in due distinti insiemi, detti schiere, ciascuno dei quali ricopre interamente la superficie.
Due rette appartenenti a una stessa schiera sono sghembe, mentre due rette appartenenti a schiere diverse sono incidenti o parallele.
Si chiama paraboloide finito la regione finita di spazio delimitata dalla superficie di un paraboloide ellittico e da un piano che interseca perpendicolarmente il suo asse. La distanza h del vertice del paraboloide dal piano di intersezione è l’altezza del paraboloide finito. Il volume di un paraboloide finito di parametri a e b e di altezza h è V = πabh /2.
Nella pratica, il paraboloide circolare, in virtù della proprietà focale della parabola, trova applicazione nella costruzione di antenne e specchi per fari o riflettori.