Cartesio, ovale di
Cartesio, ovale di
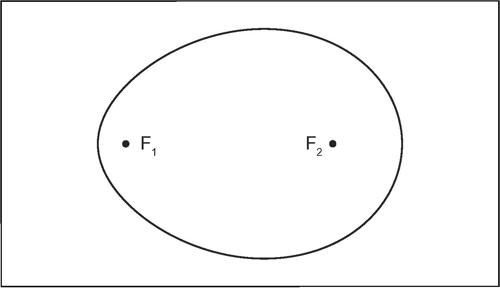
Cartesio, ovale di curva algebrica piana del quarto ordine ottenuta come luogo dei punti P del piano tali che le loro distanze da due punti fissi, moltiplicate per due numeri m e n dati, hanno somma costante. L’equazione si scrive
essendo F1 e F2 due punti fissi, detti fuochi, e m, n, k numeri reali non nulli. Può essere considerato una generalizzazione di conica a centro proprio; infatti, se risulta m = n e k è concorde con m e n, si ha un’ellisse o un insieme vuoto di punti, se invece risulta m = −n, si ha un’iperbole o un insieme vuoto di punti. In realtà, Cartesio la studiò nel caso particolare in cui m = 1 e n = 2; in tale caso la curva assume la forma di un uovo. Se si considera il caso generale, la relazione del luogo può essere scritta come
e, in un riferimento cartesiano (con i fuochi nei punti F1(1, 0) e F2(1, 0)), la sua equazione, con due successive elevazioni al quadrato, è
avendo posto c = a2 − b2 e d = a2 + b2. Occorre osservare che il luogo dei punti le cui coordinate soddisfano l’equazione algebrica precedente, poiché è stata ottenuta con successive elevazioni al quadrato, fornisce non uno ma due ovali, l’uno interno all’altro, e non descrive quindi esattamente il luogo così come è stato definito geometricamente. Gli ovali di Cartesio sono curve anallagmatiche, ovvero invarianti per inversioni circolari (→ anallagmatico).