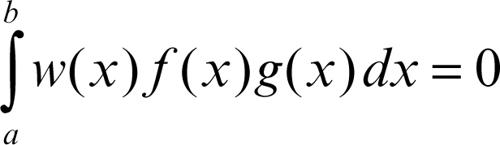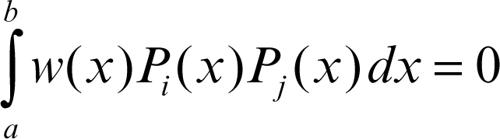ortogonalita

ortogonalita

ortogonalità in geometria elementare è sinonimo di → perpendicolarità. Nella sua accezione più semplice il termine è riferito a due rette di un piano che si intersecano formando quattro angoli retti e, a partire da questa definizione, viene esteso nel piano a segmenti e curve, nello spazio a rette, piani, curve e superfici. In generale si stabilisce la relazione di ortogonalità tra due oggetti geometrici a e b quando una opportuna retta o un opportuno piano associato all’oggetto a risulta ortogonale a una opportuna retta o a un opportuno piano associato all’oggetto b. La relazione di ortogonalità tra due oggetti geometrici non è una relazione di equivalenza. Nello spazio euclideo, una retta r e un piano π risultano ortogonali se hanno un punto A in comune e la retta r è ortogonale a ogni retta di π passante per A. Due piani π e π′ dello spazio euclideo sono ortogonali se esiste in uno dei due piani una retta ortogonale all’altro piano. Introdotto un riferimento cartesiano, si dicono condizioni di ortogonalità le relazioni numeriche esistenti tra i coefficienti delle equazioni di due rette, o di due piani che devono essere soddisfatte perché tali elementi siano tra loro perpendicolari. Due rette del piano, di rispettive equazioni ax + by + c = 0 e a′x + b′x + c′ = 0, sono ortogonali se e solo se risulta aa′ + bb′ = 0, condizione equivalente a mm′ + 1 = 0 se le rette sono assegnate mediante le equazioni esplicite y = mx + q e y =m′x + q′ e m e m′ sono quindi i loro coefficienti angolari.

Due vettori dello spazio euclideo sono ortogonali se e solo se il loro prodotto scalare risulta nullo. Due vettori v₁ = (x₁, y₁, z₁) e v₂ = (x₂, y₂, z₂) dello spazio euclideo sono pertanto ortogonali se e solo se risulta x₁x₂ + y₁y₂ + z₁z₂ = 0.

Ciò permette di caratterizzare analiticamente l’ortogonalità tra rette e piani. In particolare risultano ortogonali:

• due rette r e r′, di rispettivi parametri direttori (l, m, n) e (l′, m′, n′), se e solo se risulta ll′ + mm′ + nn′ = 0;

• una retta r di parametri direttori (l, m, n) e un piano π di equazione ax + by + cz + d = 0, se e solo se il rango della matrice formata dai tre parametri e dai tre coefficienti risulta uguale a 1;

• due piani, di rispettive equazioni ax + by +cz + d = 0 e a′x + b′y + c′z + d′ = 0, se e solo se risulta aa′ + bb′ + cc′ = 0.

La nozione di ortogonalità può essere estesa a curve e superfici riferendosi all’ortogonalità tra rette e piani a esse tangenti. In particolare due curve sono ortogonali in un punto P a esse comune se tali sono le rispettive tangenti in P; analogamente, due superfici si dicono ortogonali quando nei loro punti di intersezione i piani a esse tangenti, e quindi le loro normali, sono fra loro perpendicolari.

☐ In analisi matematica, due funzioni ƒ e g definite in un intervallo [a, b] a valori reali si dicono ortogonali nel senso di L²(a, b) (→ spazio L^p(Ω)) rispetto alla funzione peso w anch’essa definita nello stesso intervallo se vale la relazione:

Risultano poi di particolare importanza le famiglie {P_i} di polinomi ortogonali rispetto a una funzione peso w. Anche in questo caso si dice che i polinomi P_i sono ortogonali fra loro se vale la relazione:

per ogni i e j. In particolare, i polinomi di → Hermite sono ortogonali rispetto alla distribuzione normale di probabilità, i polinomi di → Čebyšëv rispetto alla funzione peso

nell’intervallo [−1, 1] e i polinomi di → Legendre rispetto alla distribuzione di probabilità uniforme nell’intervallo [−1, 1].

☐ In geometria cartesiana, un sistema di riferimento è ortogonale, se tali sono i suoi assi.

☐ In algebra lineare, è detta ortogonale una matrice quadrata invertibile la cui trasposta coincide con la sua inversa (→ matrice); due vettori sono detti ortogonali se il loro prodotto scalare è uguale a 0; una base di uno spazio vettoriale è ortogonale se i vettori che la compongono sono mutuamente ortogonali (si vedano → vettore; → prodotto hermitiano).

☐ Per altri diversi contesti si vedano: → involuzione ortogonale; → proiezione ortogonale; → sottospazio ortogonale; → traiettoria ortogonale.