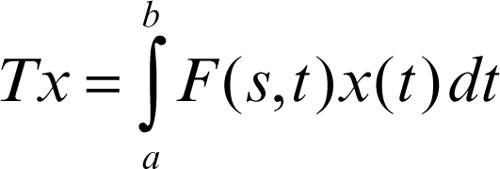operatore
operatore
operatore termine che, in senso lato, è sinonimo di funzione e può riferirsi a numeri, insiemi, funzioni, spazi ecc. Sono operatori tutte le funzioni, l’operatore derivata, l’operatore integrale e molti altri, ma anche una frazione può essere intesa come operatore quando, moltiplicata per un numero, lo trasforma.
Operatore lineare
Applicazione T di uno spazio vettoriale X in uno spazio vettoriale Y, entrambi sullo stesso campo K per la quale risulta
per tutti i punti x1 e x2 di X e per ogni scalare a, b di K. Se lo spazio Y è il campo K si parla di → funzionale. Se X e Y sono dotati di struttura topologica, l’operatore T si dice continuo in un punto x0 di X se per ogni intorno V di Tx0 esiste un intorno U di x0 tale che Tx appartiene a V per tutti gli x di X appartenenti a U. Un operatore è detto continuo in X se è continuo in tutti i punti di X. Un operatore lineare è detto limitato se trasforma insiemi limitati in insiemi limitati. Ogni operatore lineare continuo è limitato; il viceversa è vero se X è metrizzabile. Un operatore T: X → Y, dove X e Y sono spazi vettoriali topologici, si dice compatto se trasforma insiemi limitati in insiemi relativamente compatti, cioè in insiemi la cui chiusura è compatta (→ compattezza). In uno spazio di dimensione finita, ogni operatore continuo è compatto. Un esempio di operatore compatto in uno spazio di dimensione infinita (lo spazio delle funzioni continue nell’intervallo [a, b] dotato della norma uniforme) è fornito dall’operatore integrale
in cui F è una funzione continua assegnata.