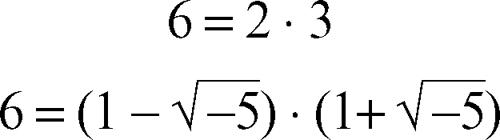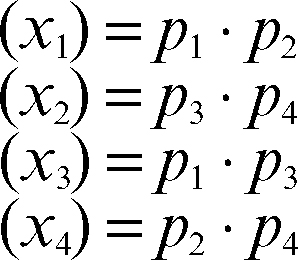numero ideale

numero ideale

numero ideale in teoria dei numeri, concetto introdotto da E.E. Kummer e che così si può precisare. Sia x un elemento dell’anello Z[z] con z numero complesso che ammetta due diverse fattorizzazioni in C, quali per esempio

Kummer dimostrò che gli elementi non nulli di Z[z] possono essere rappresentati come elementi di un semigruppo moltiplicativo D nel quale la scomposizione in fattori primi è però unica. Quindi, per ogni x non nullo di Z[z], la sua immagine (x) in D risulterà scomponibile in modo unico in fattori primi ideali, che non sono necessariamente immagini di qualche elemento di Z[z].

L’esistenza di due tali scomposizioni distinte può spiegarsi così: esistono dei numeri ideali p₁, p₂, p₃, p₄ tali che:

In tali espressioni le parentesi tonde indicano gli ideali principali generati dai rispettivi elementi e le due scomposizioni, che differiscono solo per l’ordine dei fattori, si scrivono