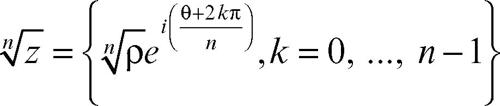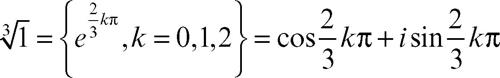numero complesso

numero complesso

numero complesso numero della forma x + iy, in cui x e y sono numeri reali e i, detto unità immaginaria, è un particolare numero complesso definito dalla relazione i ² = −1. I numeri immaginari, così chiamati da Cartesio, furono introdotti nella prima metà del xvi secolo da alcuni algebristi italiani, tra cui N. Tartaglia, S. Dal Ferro e R. Bombelli, come artifici utili per determinare le soluzioni reali di alcune equazioni di grado superiore al secondo; solo successivamente, soprattutto con A. de Moivre, Eulero e C.F. Gauss (cui si deve il termine numero complesso), se ne accettò la piena legittimità di numeri, soprattutto dopo che, con J.R. Argand, fu data una loro semplice ed esauriente interpretazione geometrica (→ Argand-Gauss, piano di).

L’insieme dei numeri complessi costituisce un campo, indicato con il simbolo C (→ C, insieme dei numeri complessi). Il campo dei numeri complessi è isomorfo al campo dei numeri reali, del quale esso è un’estensione; inoltre, non è ordinato, ossia non esiste nessuna relazione d’ordine, compatibile con le operazioni, che lo renda tale (non ha senso scrivere disuguaglianze tra numeri complessi). Se z = x + iy è un numero complesso, allora i numeri reali x e y sono detti rispettivamente parte reale di z, indicata con il simbolo Re(z), e parte immaginaria di z, indicata con il simbolo Im(z). Un numero complesso non nullo z della forma z = iy, cioè tale che Re(z) = 0, è detto puramente immaginario o immaginario puro o, semplicemente, numero immaginario. I numeri con parte immaginaria nulla si identificano con i numeri reali.

Come estensione delle operazioni tra i numeri reali, nell’insieme dei numeri complessi si definiscono addizione e moltiplicazione. Se z₁ = x₁ + iy₁ e z₂ = x₂ + iy₂ si ha:

• z₁ + z₂ = (x₁ + x₂) + i (y₁ + y₂)

• z₁ ⋅ z₂ = (x₁x₂ − y₁y₂) + i (x₁y₂ + y₁x₂)

L’opposto di z = x + iy è il numero −z = −x − iy mentre l’inverso moltiplicativo del numero z, diverso da 0, è

Due numeri complessi che abbiano uguali le parti reali e opposte le parti immaginarie sono detti coniugati: se z = x + iy, allora il coniugato di z è il numero complesso z̄ = x – iy. L’operazione che a un numero complesso z associa il suo coniugato è detta coniugio e gode delle seguenti proprietà, dove z e w indicano due arbitrari numeri complessi:

• z + z̄ = 2Re(z)

• z − z̄ = 2Im(z)

• z̄ = z se e solo se Im(z) = 0, cioè se e solo se z è un numero reale

• zz̄ è un numero reale positivo o nullo

• zz̄ = 0 se e solo se z = 0.

La rappresentazione geometrica dei numeri complessi in un piano dotato di riferimento cartesiano si ottiene associando al numero complesso z = x + iy il punto del piano di coordinate (x, y). Secondo tale corrispondenza, i numeri reali sono rappresentati dai punti dell’asse delle ascisse mentre i numeri puramente immaginari dai punti dell’asse delle ordinate; il prodotto zz̄ coincide con la norma del vettore (x, y) nel piano, vale cioè l’uguaglianza zz̄ = x ² + y ².Si definisce pertanto la norma del numero complesso z (indicata con il simbolo ‖z‖) come il numero reale positivo x ² + y ² e il modulo di z (indicato con il simbolo |z|) come il modulo del vettore (x, y), vale a dire come il numero reale positivo

Se nel piano di Argand-Gauss, dotato di un sistema di riferimento Oxy, si fissa un sistema di coordinate polari centrato nell’origine, con l’asse polare coincidente con il semiasse reale positivo, allora ogni numero complesso non nullo z = x + iy ha una rappresentazione polare e può essere scritto nella forma goniometrica z = ρ(cosθ + i senθ), dove

è il modulo di z e dove θ è l’anomalia del punto (x, y), più propriamente detta in questo caso argomento di z. È bene osservare che, dato un numero complesso z ≠ 0, il suo argomento è definito a meno di un multiplo di 2π: ci si restringe allora all’intervallo (−π, π] e si parla di argomento principale di z, indicato con Arg(z). In particolare, dato un numero complesso non nullo z = x + iy, si ha:

• per x = 0 e y > 0: Arg(z) = π/2

• per x = 0 e y < 0: Arg(z) = −π/2

• per x > 0: Argz = arctan(y/x)

• per x < 0 e y > 0: Arg(z) = Arg(−z) + π

• per x < 0 e y < 0: Arg(z) = Arg(−z) −π

In modo più intrinseco, la scrittura goniometrica di un numero complesso può essere espressa ricorrendo alla funzione esponenziale nel campo complesso ristretta all’asse immaginario: essa ha infatti la descrizione parametrica e^it = cos(t) + isin(t), dove t indica un parametro reale, ed è dunque periodica di periodo 2π. Pertanto, se z è un arbitrario numero complesso non nullo e se ρ e θ indicano rispettivamente il suo modulo e il suo argomento, si può riscriverne la forma goniometrica in modo compatto nella forma z = ρe^iθ.

La rappresentazione goniometrica è molto utile per descrivere la moltiplicazione tra numeri complessi: se infatti

allora vale

cioè il modulo del prodotto è il prodotto dei moduli e l’argomento del prodotto è la somma degli argomenti.

In particolare, se z = ρe ^{i θ} e se n è un arbitrario numero intero, vale allora zⁿ = ρⁿe ⁱⁿθ e si definisce così la potenza di un numero complesso a esponente naturale, che può essere estesa a qualunque esponente razionale.

Come s’è detto, l’unità immaginaria i soddisfa la fondamentale relazione i ² = −1. Per questa ragione si scrive anche i = √(−1). Da questo fatto segue che ogni numero complesso (e in particolare ogni numero reale, positivo o negativo che sia) ammette due radici quadrate complesse. In virtù del teorema fondamentale dell’algebra, ogni numero complesso z ammette n radici n-esime; se inoltre esso è diverso da 0, allora le sue n radici n-esime sono distinte. Sfruttando la rappresentazione goniometrica, è possibile dare un’elegante descrizione dell’insieme delle radici n-esime di un numero complesso z. Se infatti z = ρe ^{i θ}, vale allora:

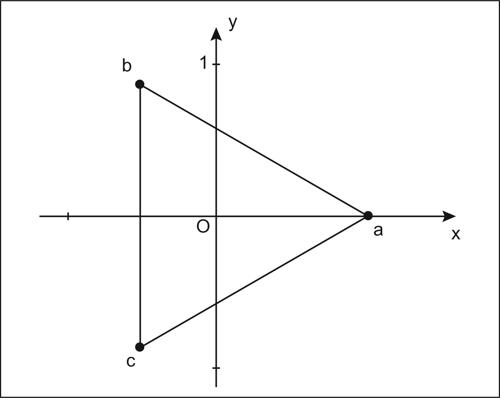
Ciò significa che, nel piano di Argand-Gauss, le → radici n-esime dell’unità sono disposte ai vertici di un poligono regolare di n vertici, il primo dei quali ha coordinate (1, 0). Per le radici cubiche di 1 si ha così:

che nel piano di Argand-Gauss sono rispettivamente rappresentate dai punti vertici di un triangolo equilatero.