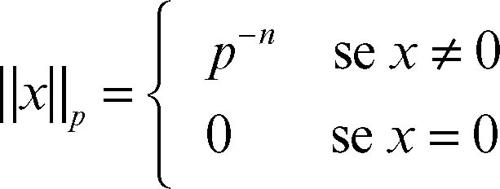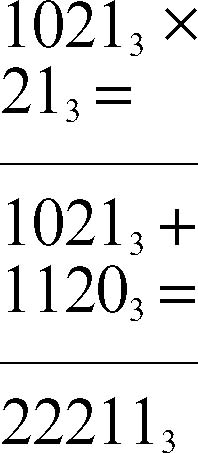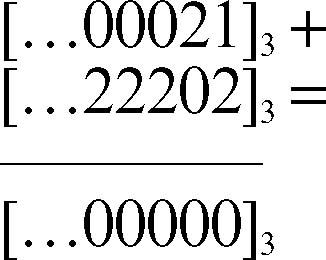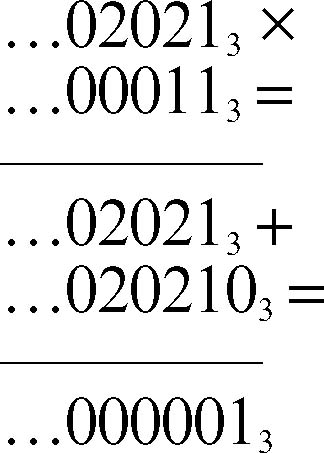numeri p-adici, insieme dei
numeri p-adici, insieme dei
numeri p-adici, insieme dei in algebra e in teoria dei numeri, insieme numerico, costruibile a partire da Q, insieme dei numeri razionali, per ogni numero primo p. Tale insieme è indicato con Qp ed è un campo che estende il campo Q dei razionali in modo differente dall’estensione che si effettua con il campo dei numeri reali R. Esso è infatti definito come il completamento metrico di Q rispetto a una opportuna metrica dp definita su Q a partire da p, e non, come R, rispetto all’ordinaria metrica euclidea (per la quale d(x, y) = |x − y|). La costruzione di tale insieme è resa possibile dal fatto che, in base al teorema fondamentale dell’aritmetica, dati un numero razionale x non nullo e un numero primo p, esiste un unico n ∈ Z tale che
essendo a e b interi non nulli e non divisibili per p. Per esempio, considerando il numero primo p = 3, si ha
oppure
oppure, ancora:
Dato un numero primo p, si definisce allora la funzione ‖...‖p: Q → R+
che soddisfa gli assiomi di una norma su Q ed è detta norma p-adica; la distanza dp associata a tale norma (definita da dp(x, y) = ‖x − y‖p) è detta distanza p-adica. L’insieme dei numeri p-adici Qp si definisce quindi come il completamento metrico di Q rispetto a tale distanza p-adica; tale insieme eredita da Q una naturale struttura di campo che estende quella già definita su Q. Se si considera il completamento metrico di Z rispetto alla distanza p-adica, si ottiene l’insieme degli interi p-adici Zp, i quali hanno tutti norma minore di 1. Tale sottoinsieme di Qp eredita da Z una naturale struttura di anello rispetto alla quale Qp ne è il campo dei quozienti. Il simbolo con cui è denotato l’anello degli interi p-adici è lo stesso con il quale spesso è denotato l’anello delle classi resto modulo p; tuttavia essi sono oggetti ben distinti.
Ogni numero p-adico ammette un’unica espansione p-adica come serie formale del tipo:
in cui m ∈ Z e ai è una cifra del sistema posizionale in base p, cioè ai ∈ N, con 0 ≤ ai ≤ p − 1 e, da un certo indice in poi, gli ai possono essere tutti uguali a 0 (→ sistema di numerazione posizionale). In notazione posizionale, la precedente serie si esprime mediante la successione dei suoi coefficienti come
vale a dire con un numero in base p il quale possiede finite cifre a destra dopo la virgola e possibilmente infinite cifre a sinistra prima della virgola. Tale scrittura è unica a meno di zeri a sinistra (possibilmente infiniti) e a destra; solitamente tali zeri vengono omessi e se m > 0 allora si omette la virgola. Se dunque nella precedente scrittura si suppone am ≠ 0, allora la norma p-adica di x si definisce come il numero ‖x‖p = p−m. All’interno delle precedenti somme formali, gli interi p-adici coincidono con le somme prive di termini negativi, vale a dire senza cifre dopo la virgola: un numero p-adico è un intero p-adico se e solo se la sua norma p-adica è minore o uguale di 1. Se x è un numero intero non negativo, la sua notazione p-adica si ricava immediatamente dalla sua scrittura posizionale in base p. Così, per esempio, con p = 3 e indicando l’espansione p-adica tra parentesi quadre, si ottengono 2510 = 2 ⋅ 32 + 2 ⋅ 31 + 1 ⋅ 30 = 2213 = [...000221]3 e, con ogni primo p, 0 = [...0000]p. I numeri p-adici corrispondenti agli interi non negativi sono tutti privi di virgola e hanno tutti infiniti zeri alla loro sinistra: essi coincidono con le somme finite prive di termini negativi.
Dati due numeri p-adici, si possono definire le operazioni di addizione e sottrazione e, conseguentemente, di moltiplicazione tenendo tuttavia conto che le operazioni vanno eseguite in base p e che occorre continuare l’operazione sulla sinistra, considerando gli eventuali riporti.
Per esempio, la moltiplicazione 34 per 7 in modalità p-adica può essere eseguita in questo modo (se p = 3):
• si riscrive 34 in modalità 3-adica: 34 = 1 ⋅ 33 + 0 ⋅ 32 + 2 ⋅ 31 + 1 ⋅ 30 = 10213 = [...0001021]3;
• si riscrive 7 in modalità 3-adica: 7 = 2 ⋅ 31 + 1 ⋅ 30 = 213 = [...00021]3;
• si effettua la moltiplicazione in colonna con l’ordinario algoritmo, ma tenendo conto che si opera in base 3 (in tale base 2 ⋅ 2 = 4 = 113 e quindi va scritto 1 in corrispondenza della colonna e riportato 1 a sinistra):
La sequenza [...00022211]3 è naturalmente il corrispondente 3-adico di 238 = 34 ⋅ 7.
L’immagine p-adica di un numero intero negativo −n si ottiene considerando che deve essere n + (− n) = 0. Perciò, per esempio, la rappresentazione 3-adica di −7, si ottiene tenendo conto che 7 = [...00021]3 e quindi −7 = [...22202]3. Infatti:
Anche i numeri razionali non interi possono essere espressi come numeri p-adici. Per far ciò si considerano dapprima le frazioni unitarie 1/n, con n intero positivo, e si tiene conto che n · (1/n) = 1, che, in notazione p-adica, è [...0001]p. Per esempio, poiché la rappresentazione 3-adica di 4 = 1 · 31 +1 · 30 è [...00011]3, in forma 3-adica la frazione 1/4 = [...a3a2a1a0]3 deve essere tale che:
Il numero 3-adico corrispondente a 1/4 è quindi [...2020202021]3, numero p-adico periodico con periodo (a sinistra) uguale a 20. Infatti,
Dalla moltiplicazione di 1/4 per 3 (che in forma 3-adica è [...00010]3) si ottiene che il corrispondente 3-adico di 3/4 è [...20202020210]3, anch’esso periodico di periodo 20.
Può accadere che un numero razionale x sia un intero p-adico: questo accade ogni qual volta x = a /b con b non divisibile per p. Ogni numero razionale di tale forma si scrive in notazione p-adica come un numero privo di virgola, finito (nel qual caso coincide con un numero intero) o infinito periodico (nel qual caso coincide con un numero non intero). Se invece x = a /b ha norma p-adica pm maggiore di 1 (vale a dire con m > 0), allora x si scrive in notazione p-adica nella forma
dove le cifre posizionali ai sono periodiche da un certo indice in poi. I numeri p-adici non razionali coincidono dunque con quei numeri p-adici (possibilmente con virgola) che sono infinti a sinistra ma non periodici.
I numeri p-adici furono introdotti da K. Hensel nel 1897 in un articolo riguardante lo sviluppo in serie di potenze dei numeri algebrici e trovano applicazione nella risoluzione delle equazioni diofantee e in altri problemi di teoria dei numeri.