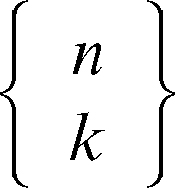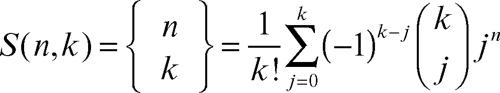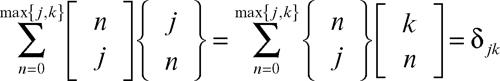Stirling, numeri di

Stirling, numeri di

Stirling, numeri di numeri che legano le potenze di un numero x (non necessariamente intero) con i corrispondenti simboli di → Pochhammer discendenti x_(n) = x(x − 1)(x − 2) … (x − n + 1). Precisamente i numeri di Stirling di prima specie s(n, k), 1 ≤ k ≤ n, sono i coefficienti dello sviluppo

mentre i numeri di seconda specie S(n, k), 0 ≤ k ≤ n, forniscono lo sviluppo inverso

(Si noti che i simboli di Pochhamer sono a volte indicati in modo diverso nei diversi contesti; quello che qui interviene è il simbolo “discendente”).

I numeri di prima specie hanno segni alternati; i loro moduli |s(n, k)| = (−1)^n−ks(n, k) si designano talvolta con il simbolo

I numeri di seconda specie sono tutti positivi, si indicano anche con

e sono dati dalla formula

Valgono inoltre le relazioni

che esprimono il fatto che le due matrici triangolari inferiori s e S formate dai numeri di Stirling fino a un prefissato intero N sono una l’inversa dell’altra.