normale
normale
normale in geometria, sinonimo di perpendicolare, dall’etimo di «norma», che significa «squadra». Espressioni quali «retta normale a un’altra retta» o «retta normale a un piano» riprendono questo significato elementare.
Nel piano, la normale a una curva in un suo punto P è la perpendicolare alla tangente alla curva in P, passante per tale punto. Se la curva piana è riferita a un sistema di riferimento cartesiano Oxy, il segmento PN in cui la normale n in P interseca l’asse delle ascisse si dice segmento di normale o più semplicemente normale; mentre il segmento PQ avente un estremo in P e l’altro nell’intersezione tra l’asse dell’ascisse e la perpendicolare a esso passante per P, è detto sottonormale. Indicata con y = ƒ(x) l’equazione della curva, la normale PN risulta essere
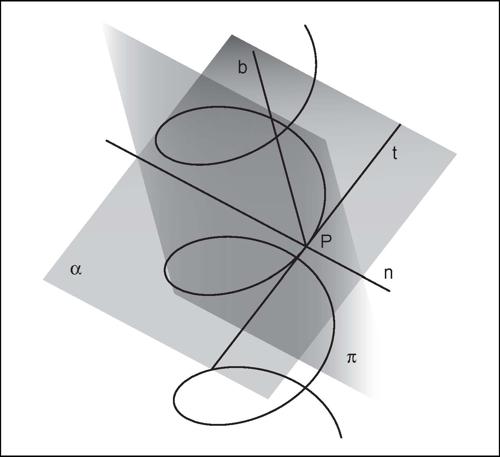
Nel caso di una curva sghemba, tutte le rette passanti per un suo punto P e perpendicolari alla tangente alla curva in P si dicono normali alla curva in P; esse costituiscono il piano normale alla curva in P. Tra le infinite normali ve ne sono due particolari: la normale principale, che appartiene al → piano osculatore alla curva in P, e la → binormale che è perpendicolare al piano osculatore alla curva in P (→ terna intrinseca).
Se il punto P appartiene a una superficie regolare S, si parla di normale per P alla superficie per indicare la normale (cioè perpendicolare) al piano tangente a S in P.
Se S è descritta da un’equazione in forma implicita come ƒ(x, y, z) = 0, la normale ha la direzione del vettore gradiente di ƒ in P. Per esempio, la normale all’ellissoide di equazione
nel suo punto A(2, 1, −2) è diretta come il vettore gradƒ(A) = (1/4)i + (1/2)j − (1/2)k; il versore è n = (i + 2j − 2k)/3.
Se le equazioni di S sono date in forma parametrica x = x(u, v), y = y(u, v), z = z(u, v), un vettore normale è dato dal prodotto vettoriale dei vettori tangenti tu = (∂x/∂u)i + (∂y/∂u)j + (∂z/∂u)k e tv = (∂x/∂v)i + (∂y/∂v)j + (∂z/∂v)k. Per esempio, data la superficie di equazioni x = u 2 + v 2, y = u 2 − v 2, z = uv, nel punto B(5, 3, 2) corrispondente a u = 2 e v = 1, si hanno i vettori tu = 4i + 4j + k, tv = 2i − 2j + 2k, il cui prodotto vettoriale è tu × tv = 10i − 6j − 16k; il versore normale è dunque (5i − 3j − 8k)/(7√(2)).
In generale, quindi, se la superficie ha equazioni parametriche xi = σi (u, v), il versore normale è dato da
denotando con σu e σv i vettori delle derivate parziali delle σi calcolate rispetto a u e a v, con × il prodotto vettoriale e con ‖...‖ la norma euclidea.
□ L’aggettivo «normale» è frequentemente utilizzato nella teoria delle equazioni per indicare, tra le infinite forme equivalenti che una equazione può assumere, quella scelta in base a criteri di semplicità o di opportunità in relazione al problema che si deve risolvere. Così, si dice che sono scritte in forma normale le equazioni ax + b = 0 o ax 2 + bx + c = 0. Anche nel calcolo degli enunciati si parla di forma normale (congiuntiva o disgiuntiva) per indicare una particolare scrittura che risponde a criteri di regolarità e semplicità.
□ In teoria dei gruppi, il sottogruppo normale è un sottogruppo con particolari proprietà; per la sua definizione si veda il lemma → sottogruppo.
□ In statistica, il termine è frequentemente utilizzato come forma abbreviata di → curva normale (si veda anche → distribuzione normale).