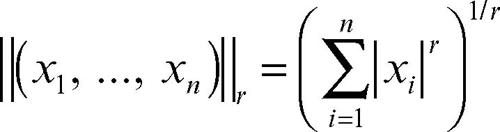norma

norma

norma applicazione ‖...‖: V → [0, +∞) definita su uno spazio vettoriale reale o complesso e caratterizzata dalle seguenti proprietà:

• ‖v‖ ≥ 0, ∀v ∈ V e ‖v‖ = 0 se e solo se v = 0;

• ‖k ⋅ v‖ = |k| ⋅ ‖v‖, ∀v ∈ V e per ogni scalare k;

• ‖u + v‖ ≤ ‖u‖ + ‖v‖, ∀u, v ∈ V.

Lo spazio V dotato di norma viene detto spazio vettoriale normato. Negli spazi vettoriali R e C la funzione valore assoluto (modulo) è una norma. Per l’insieme C si veda il lemma → numero complesso, norma di un. L’esempio tipico di norma nello spazio Rⁿ è la norma euclidea, così definita:

Ogni prodotto scalare definito positivo induce una norma mediante

In uno stesso spazio possono essere definite più norme; per esempio in Rⁿ e in Cⁿ si può introdurre per ogni 1 ≤ r < +∞ la seguente norma:

che per r = 2 coincide con la norma euclidea.

Se lo spazio vettoriale ha dimensione finita si dimostra che queste norme sono tutte equivalenti: precisamente, due norme ‖...‖ e ‖...‖* sullo stesso spazio si dicono equivalenti se esistono due costanti k e K, positive, tali che k‖v‖ ≤ ‖v‖* ≤ K‖v‖ per ogni elemento v dello spazio vettoriale. Per esempio, in R ⁿ e C ⁿ si può definire, oltre alle già citate r-norme, anche una norma infinito:

In uno spazio normato V resta naturalmente definita una metrica definendo la distanza mediante d(u, v) = ‖u − v‖, ∀u, v ∈ V, e quindi una topologia, definendo come intorno di v qualsiasi insieme contenente una palla (→ disco topologico) aperta B_k = {u ∈ V : ‖u − v‖ < k}, con k > 0.

Tutte le norme definibili in uno stesso spazio vettoriale di dimensione n sono equivalenti e definiscono la stessa struttura topologica, equivalente alla topologia standard euclidea di Rⁿ.

Norma di una matrice

Nello spazio vettoriale delle matrici reali quadrate di ordine n, una norma è detta compatibile con una assegnata norma vettoriale in Rⁿ se:

• ‖Av‖ ≤‖A ‖ ⋅·‖v‖ per ogni matrice A e ogni vettore v;

• ‖AB ‖ ≤‖A ‖ ⋅·‖B‖.

A una stessa norma vettoriale possono essere associate diverse norme con essa compatibili. Una norma compatibile è detta indotta dalla norma vettoriale se per ogni A esiste un v ≠ 0 tale che la prima delle due disuguaglianze precedenti valga come uguaglianza. Per ogni norma vettoriale esiste almeno una norma indotta,

detta norma naturale: per esempio la norma euclidea induce la norma naturale

dove AT indica la trasposta di A e λ è il massimo autovalore della matrice ATA. Ogni norma naturale costituisce una limitazione superiore per il raggio spettrale di A: λ(A) ≤‖A ‖.

Norma in statistica

In statistica il termine norma è sinonimo di → moda, è cioè il valore più frequente in una distribuzione di dati.

Norma in analisi funzionale

Il concetto di norma è anche utilizzato in questa branca dell’analisi dove si studiano le proprietà degli spazi normati e completi nella metrica indotta dalla norma (spazi di Banach). In particolare, negli spazi di dimensione infinita si studiano le proprietà delle applicazioni lineari, non lineari e le proprietà di compattezza, cioè le condizioni che garantiscono la convergenza, per esempio, di successioni limitate; infatti, in dimensione infinita gli insiemi chiusi e limitati non sono in generale insiemi compatti.