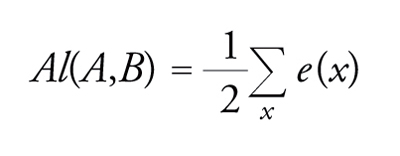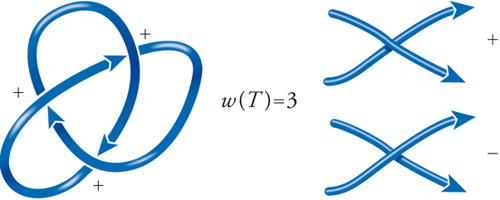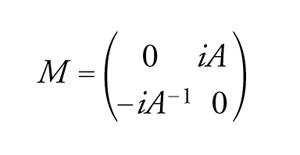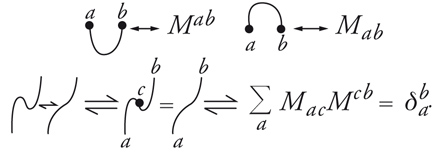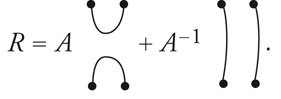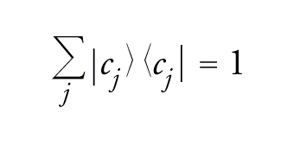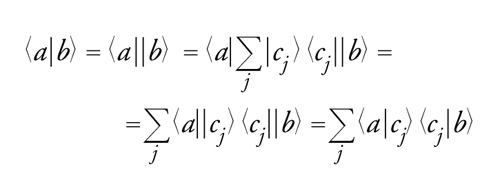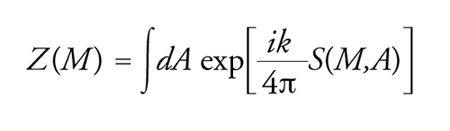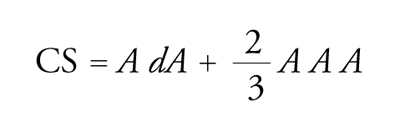Nodi e fisica
Nodi e fisica
Nel secolo scorso lord Kelvin (William Thomson) ideò la cosiddetta teoria degli atomi vortice in cui gli atomi erano visti come mulinelli nell'etere, che si supponeva riempisse lo spazio. I mulinelli tridimensionali avrebbero dovuto soddisfare alcune condizioni per essere considerati atomi: in particolare, avrebbero dovuto essere stabili nel tempo e interagire tra loro in modo da originare molecole. Lord Kelvin immaginava questi mulinelli come anelli di fumo in tre dimensioni: un anello di fumo ha la forma di una ciambella, che si muove e ruota su se stessa mentre si sposta nello spazio. Nel caso più generale, egli suppose che più ciambelle fossero annodate singolarmente o, eventualmente, l'una all'altra. La possibilità di un annodamento reciproco corrispondeva al caso in cui singoli atomi si legassero tra loro per formare molecole; la forma a laccio chiuso ne garantiva la stabilità.
Lord Kelvin scrisse numerosi articoli sulla teoria degli atomi vortice e coinvolse i matematici Peter G. Tait, T. P. Kirkwood e Charles N. Little in un progetto per la compilazione di tavole di tutti i nodi topologicamente distinti. Si trattava di un compito enorme e, ovviamente, infinito, a meno di non introdurre alcune restrizioni. Tait, Kirkwood e Little si limitarono a nodi la cui proiezione nel piano avesse al più dieci incroci; esistono tuttavia ben 49 nodi con nove incroci e oltre 100 con dieci. Essendo i primi matematici a occuparsi di nodi, essi compilarono le loro tavole per tentativi ed errori: non possedevano infatti procedimenti di calcolo per determinare se un nodo fosse effettivamente annodato o se due nodi fossero realmente distinti. Queste tecniche vennero sviluppate molto più tardi, ma l'esigenza di distinguere i nodi dal punto di vista topologico nacque proprio dal loro tentativo di enumerazione degli atomi vortice di lord Kelvin.
La teoria degli atomi vortice scomparve quando la teoria della relatività speciale di Einstein dimostrò l'inutilità dell'etere. Tuttavia, i vortici annodati continuano a essere oggetto di studio e di recente il fisico Herbert Jehle ha anche suggerito che le particelle elementari possano essere modellate da un flusso elettromagnetico annodato e quantizzato. Anche nella teoria delle stringhe le particelle elementari sono viste come anelli chiusi, ma parlare di annodamento di questi anelli in senso tridimensionale è problematico, perché la loro condizione naturale è quella di vagare in spazi con più di tre dimensioni.
Di seguito si tratteggeranno alcune delle tecniche fondamentali della teoria dei nodi (sconosciute a Tait, Kirkwood e Little) e la loro relazione con alcuni aspetti della fisica moderna. Tale correlazione fu stabilita all'inizio degli anni Ottanta del secolo scorso, quando l'autore riuscì a trovare il modo di descrivere il polinomio di Alexander (e più tardi il polinomio di Jones) nella forma di una funzione di partizione della meccanica statistica, e Vaughan F.R. Jones scoprì invarianti del tutto nuovi di nodi e link direttamente correlati a problemi di meccanica statistica. Pochi anni più tardi, Edward Witten mostrò come tutte queste costruzioni potessero essere comprese in termini di teoria quantistica dei campi, dando con ciò origine al nuovo settore di studio della topologia quantistica e della teoria topologica dei campi quantizzati.
Come fissare un nodo: le mosse di Reidemeister
Cominciamo ora a costruire qualche nodo. Considereremo in particolare il nodo detto gassa d'amante, piuttosto utile nella pratica per esempio per chi voglia fissare la briglia di un cavallo a una staccionata o una barca a un molo. Il lettore potrebbe forse già avere familiarità con le convenzioni delle figure, con cui si rappresentano le istruzioni per annodare una corda: le soluzioni di continuità in una linea indicano dove la linea passa al di sotto di un'altra, cosicché l'incrocio di due tratti di corda è indicato come nella fig. 2A. Abbiamo così costruito un linguaggio, quello dei diagrammi di nodo, che gode della notevole proprietà di contenere implicitamente tutte le proprietà fisiche e topologiche del nodo che rappresenta, le quali tuttavia non divengono immediatamente evidenti a meno che non si costruisca effettivamente il nodo con un pezzo di corda.
In questo lavoro ci concentreremo sui metodi per ottenere le informazioni topologiche sui nodi direttamente dai loro diagrammi. Una proprietà di un nodo è detta topologica, se non dipende dal materiale con cui il nodo è costruito, né da quanto questo materiale sia stirato o piegato, purché non venga lacerato. Poiché non vogliamo rischiare di perdere il nodo nel corso di questo processo di deformazione, come succederebbe a causa di uno scivolamento sopra un estremo del pezzo di spago, adottiamo la convenzione, usuale nella teoria dei nodi, che il nodo si trovi su un anello chiuso. Il nodo a trifoglio, mostrato nella fig. 2B, è il primo esempio di anello chiuso annodato. Un nodo presentato come anello chiuso è un oggetto robusto, che può essere spostato e rigirato nello spazio in molte forme diverse ma topologicamente equivalenti. Per esempio, il lettore non dovrebbe avere difficoltà a riconoscere che il nodo mostrato nella fig. 2C è topologicamente equivalente al nodo a trifoglio della fig. 2B.
Trovandoci di fronte a questo numero potenzialmente infinito di versioni di un dato nodo o link, vediamo qui emergere un vero problema matematico. Dire che un anello è annodato significa dire che nessuna delle infinite forme che esso può assumere è quella di un anello non annodato. Il risultato chiave che sta alla base di una teoria combinatoria dei nodi è il teorema di Kurt Reidemeister, secondo il quale due diagrammi rappresentano lo stesso tipo di nodo se e soltanto se si possono ottenere l'uno dall'altro tramite una successione finita di deformazioni speciali, dette mosse di Reidemeister (fig. 3). Le mosse descritte nella fig. 3 sono rappresentative di modificazioni che si possono eseguire in diagrammi più grandi; come mostrato nella figura, esse modificano il diagramma solo localmente. Per esempio, la fig. 4A mostra una successione di mosse di Reidemeister che trasforma l'uno nell'altro due diagrammi del nodo a trifoglio. Reidemeister ha dimostrato che queste mosse colgono in modo combinatorio la nozione di isotopia ambiente dei nodi nello spazio tridimensionale. Questo significa che, pensando ai diagrammi di nodo come a fotografie istantanee, se due nodi si possono trasformare l'uno nell'altro, allora anche le loro istantanee possono essere trasformate l'una nell'altra tramite una sequenza finita di mosse di Reidemeister.
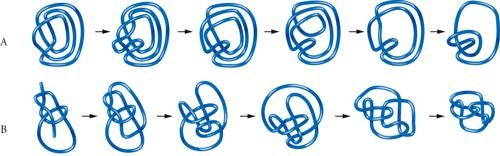
Concludiamo questo argomento con un'altra illustrazione. Prendiamo la gassa d'amante e chiudiamola a formare un anello. Una deformazione rivela allora che questa forma chiusa della gassa d'amante è topologicamente equivalente a due trifogli reciprocamente agganciati, come mostrato nella fig. 4B. Questa deformazione è stata scoperta chiudendo ad anello la corda con la quale si era costruita una gassa d'amante e giocandoci fino a che non sono apparsi due trifogli agganciati. Dopo averla scoperta, c'è voluto qualche tempo per trovare il cammino grafico dalla gassa d'amante chiusa alla coppia di trifogli agganciati mostrato nella fig. 4B, che non è difficile espandere in una successione di mosse di Reidemeister. In questi termini possiamo pensare al modello di corda del nodo come a un calcolatore analogico, che può suggerire, a chi si occupa di teoria dei nodi, successioni di deformazioni che potrebbero essere altrimenti trascurate.
Abbiamo in questo modo curiosamente capovolto il punto di vista originale: l'oggetto fisico che all'inizio era l'argomento di studio è divenuto uno strumento di calcolo per ottenere informazioni sulla matematica dei nodi. Naturalmente si tratta di un percorso a doppio senso: la chiave di questa corrispondenza risiede in quella tra il modello matematico dei nodi e le proprietà topologiche di un nodo reale. In questo senso possiamo anche vedere i nodi come analoghi ai numeri interi: così come siamo portati a credere che l'enumerazione di collezioni di oggetti stabili nel mondo sensibile obbedisca alle leggi dell'aritmetica, così dobbiamo credere che le proprietà topologiche delle corde annodate nella realtà sperimentale seguano le leggi della topologia dei nodi.
Invarianti di nodi e link: un primo passo
Utilizzare le mosse di Reidemeister come base tecnica per sviluppare la teoria dei nodi è un compito laborioso: da principio non è affatto chiaro come ottenere informazioni che siano invarianti rispetto alle mosse. Ed è l'invarianza quello che ci sta a cuore: vorremmo poter calcolare numeri (o entità algebriche come polinomi) a partire da un qualsiasi diagramma di un link, in modo tale che questi numeri non cambino quando un diagramma è modificato tramite una mossa di Reidemeister. Trovare siffatti invarianti significa trovare le informazioni topologiche sui nodi o sui link. L'esempio più semplice di un tale invariante è il numero di allacciamento di due curve: esso misura quante volte una curva orientata si avvolge intorno a un'altra. Se le curve A e B sono rappresentate in un diagramma di link a due componenti, il numero di allacciamento Al è definito dalla formula
[1] formula,
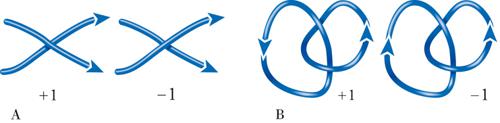
dove la somma è eseguita al variare degli incroci x di A con B, ed e(x) indica il segno dell'incrocio, definito come +1 o −1 secondo la convenzione descritta nella fig. 5A. Naturalmente, due anelli allacciati semplicemente hanno numero di allacciamento +1 o −1, come mostrato nella fig. 5B.
È facile vedere che il numero di allacciamento è in effetti invariante rispetto alle mosse di Reidemeister: non varia certamente con la prima mossa, giacché gli incroci di una componente con sé stessa non compaiono nella somma; la seconda mossa crea o distrugge due incroci di segno opposto; la terza mossa, infine, permuta una configurazione d'incroci senza modificarne i segni. In forza di queste osservazioni abbiamo dunque dimostrato che gli anelli allacciati semplicemente sono in effetti allacciati: non può esistere nessuna successione di mosse di Reidemeister che trasformi due anelli allacciati in due anelli separati, poiché il numero di allacciamento di due anelli separati è nullo.
Il polinomio di Jones
Discutiamo in questo paragrafo di un invariante di nodi e link di natura alquanto diversa. Si tratta di un invariante polinomiale scoperto da Vaughan F.R. Jones: questo invariante, indicato generalmente con VK(t), è un polinomio nella variabile t1/2 e nella sua inversa t−1/2 (ciò si esprime dicendo che VK(t) è un polinomio di Laurent in t1/2).
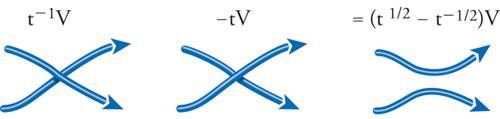
Assiomi per il polinomio di Jones. (a) Se due link orientati, K e K′, sono collegati da una isotopia ambiente, allora VK(t)=VK′(t); (b) se U è un anello snodato, allora VU(t)=1; (c) siano K+, K− e K0 tre link orientati con diagrammi che differiscono, come specificato nella fig. 6, solo in una piccola regione del piano, nella quale K+ e K− hanno un incrocio e K0 non ne ha; allora vale la formula
[2] t −1 ∙VK+(t) − t ∙VK−(t) = (t1/2−t−1/2)VK0(t).
Si noti che nella figura, invece che limitarci a specificare esattamente cosa siano K+, K− e K0, abbiamo simbolicamente espresso la formula che lega i valori di V, tracciando soltanto piccole regioni dei diagrammi con la convenzione che essi coincidano nelle parti non mostrate. Un fatto che ha reso fin da subito il polinomio di Jones una scoperta estremamente eccitante per i teorici dei nodi è che esso permette di individuare la differenza tra molti nodi e le loro immagini speculari. In seguito sono emerse altre interessanti proprietà: per esempio, esso è stato uno strumento chiave per la dimostrazione di proprietà dei link alternanti (e di loro generalizzazioni) che erano state congetturate già nel secolo scorso. A tutt'oggi, non sono noti esempi di nodi di cui il polinomio di Jones non riconosca l'annodamento. Ciò suggerisce la seguente congettura: se un singolo anello di un nodo K è effettivamente annodato, allora VK(t) non è uguale a 1.
In altre parole, è concepibile che il polinomio di Jones sia capace di determinare la proprietà di effettivo annodamento. È tuttavia noto che esso non è uno strumento di classificazione completo: esistono coppie di nodi che hanno il medesimo polinomio di Jones ma che non possono essere collegati da una isotopia ambiente, ovvero sono topologicamente diversi. Una tale coppia è costituita dai nodi di Kinoshita-Terasaka e di Conway, ed è illustrata nella fig. 7.
Il calcolo del polinomio di Jones, a partire dai suoi assiomi, non spiega perché questo invariante funzioni. L'analisi di questo metodo di calcolo permette di dimostrare che esso non dipende dalle scelte fatte e che fornisce informazioni sul nodo o sui link in esame. Un metodo alternativo porta a un'elegante formulazione del polinomio di Jones in termini di una somma sugli stati del diagramma. In tale formulazione il polinomio è ben definito fin dall'inizio ed è evidente che l'invarianza topologica nasce dall'aggiustamento di alcuni parametri di funzioni ben definite.
Il polinomio di Kauffman come somma sugli stati
Secondo gli sviluppi più recenti della teoria, si tende a considerare il diagramma di un nodo come analogo a un sistema fisico, del quale viene calcolata una funzione di partizione o somma sugli stati. La funzione di partizione è una somma di certe valutazioni su tutti i possibili stati del sistema, dove il termine stato andrà inteso in modo opportuno. Gli stati non sono le varie configurazioni che vengono assunte nel corso di un'evoluzione (deformazione topologica) a partire da una data situazione: sono invece modi di configurare la situazione presente. La funzione di partizione fornisce informazioni sulle evoluzioni topologiche del sistema, senza che queste compaiano effettivamente. Per fornire un esempio di come si possa mettere in pratica questa idea della valutazione, descriviamo ora la più semplice somma sugli stati per nodi e link che risulti significativa: il polinomio bracket (il termine bracket indica le particolari parentesi ad angolo introdotte da Paul A.M. Dirac). Prendiamo in considerazione nodi e link non orientati, e a ogni incrocio di un diagramma associamo due stati che identifichiamo con le etichette A e B, come mostrato nella fig. 8. Nello stato A vengono connesse tra loro le regioni del piano spazzate da una rotazione in senso antiorario dell'arco che sta sopra, mentre nello stato B vengono connesse quelle spazzate da una rotazione in senso orario del medesimo arco.
Uno stato S di un diagramma K consiste nella scelta di uno stato locale per ciascuno dei suoi incroci, cosicché un diagramma con n incroci avrà 2n stati. Due stati S e S′ del diagramma del nodo a trifoglio sono indicati nella fig. 9.
Utilizzeremo due valutazioni per uno stato S, indicate rispettivamente con ⟨K ∣S⟩ e con ∣∣S∣∣. Quest'ultima è chiamata norma dello stato ed è definita come il numero di curve chiuse che compongono S meno uno; così nell'esempio di cui sopra si ha ∣∣S∣∣=1 e ∣∣S′∣∣=0. La valutazione ⟨K ∣S⟩ è definita come il prodotto di tutte le etichette A o B nello stato; nell'esempio precedente si ha allora ⟨K ∣S⟩=A3 e ⟨K ∣S′⟩=A2B. Utilizzando variabili A, B e d definiamo la somma sugli stati associata al diagramma K mediante la formula seguente:
[3] formula.
In altre parole, per ogni stato S prendiamo il prodotto delle etichette che si trovano in S moltiplicato per d, elevato alla potenza ∣∣S∣∣. Si può dimostrare che questa somma sugli stati è invariante rispetto alla seconda e terza mossa di Reidemeister, purché si scelga B=1/A e d=−(A2+B2). Abbiamo dunque quasi trovato un invariante di nodo nel senso stretto del termine. Cosa succede ora se si considera la prima delle mosse di Reidemeister? Scopriamo facilmente che il bracket non è invariante rispetto alla prima mossa, il che potrebbe sembrare un inconveniente ma in ultima analisi non lo è affatto. Prima di tutto, non è difficile sistemare le cose con un piccolo aggiustamento: sia K un nodo o link orientato e definiamo l'avvolgimento (writhe) di K, denotato con w(K), come la somma di tutti i segni degli incroci di K. Come mostrato nella fig. 10, il nodo a trifoglio destrogiro ha avvolgimento 3. L'avvolgimento ha il seguente comportamento rispetto alle mosse di Reidemeister: (a) è invariante rispetto alla seconda e alla terza mossa; (b) cambia di +1 o −1 rispetto alla prima delle mosse, come illustrato di seguito:
[4] formula
Ne deduciamo che l'avvolgimento, che pure abbiamo definito in modo assolutamente elementare, si comporta in modo parallelo a quello del bracket, e possiamo combinare i due oggetti in un nuovo calcolo il cui risultato sia invariante rispetto a tutte e tre le mosse di Reidemeister. Questo nuovo invariante completo, che sarà chiamato f-polinomio, viene definito per un nodo o link orientato K tramite la seguente formula:
[5] fK (A) = (−A3)−w(K) ∙ ⟨ K ⟩(A)
dove, ricordiamo, w(K) è la somma dei segni degli incroci di K, e ⟨K⟩ è il bracket calcolato sul nodo o link ottenuto da K ignorando l'orientazione. A meno di questa normalizzazione, il bracket fornisce un modello per il polinomio di Jones originale, cui è legato dalla seguente relazione:
[6] VK (t) = fK(t−1/4).
Meccanica quantistica e topologia
Nel precedente paragrafo abbiamo stabilito come il modello bracket del polinomio di Jones sia ottenuto considerando il nodo come un sistema fisico. Questo approccio alla teoria dei nodi è suscettibile di diverse interpretazioni e in questo paragrafo ne illustreremo qualitativamente una. Immaginiamo che lo spazio sia bidimensionale, invece che tridimensionale come quello in cui viviamo. Poiché lo spazio occupa due sole dimensioni, possiamo immaginare lo spazio-tempo come tridimensionale, generato da un piano che si muove, e le tracce di punti in moto nel piano diventano le linee di universo dei punti nello spazio-tempo. Consideriamo alcuni esempi semplici. Potrebbe accadere di vedere due particelle che girano l'una attorno all'altra: nella descrizione spazio-temporale di questo moto vediamo le due linee di universo che si avvolgono l'una intorno all'altra a formare una treccia semplice. Ancora, può accadere che l'energia dello spazio vuoto dia origine a due particelle: la linea di universo corrispondente alla creazione di una coppia di particelle, come si vede nella fig. 11A, appare come una coppa, ovvero una curva con un minimo a un determinato istante. Ma può anche accadere che due particelle si annichilino a vicenda: nello spazio-tempo tridimensionale la sparizione di una coppia di particelle è rappresentata da un cappello, come mostrato nella fig. 11B, vale a dire da una curva che presenta un massimo a un determinato istante. Qualsiasi processo elementare di interazione si riflette, nel nostro spazio-tempo a tre dimensioni, in un attorcigliamento (a destra o a sinistra), una coppa o un cappello, il cui susseguirsi determina, sempre nello spazio-tempo, nodi e link come mostrato nella fig. 12.
Nella meccanica quantistica ci si può porre la domanda: qual è l'ampiezza di probabilità (non si tratta di una vera e propria probabilità, ma piuttosto di una generalizzazione della probabilità che i fisici chiamano ampiezza) che certe particelle appaiano dal vuoto, si muovano nello spazio-tempo tridimensionale seguendo il cammino corrispondente a un certo nodo o link e poi se ne tornino nel vuoto? La risposta a questa domanda è che tale ampiezza è proprio un valore del polinomio bracket del nodo. Possiamo ora descrivere il modello del bracket come ampiezza di probabilità specificandone le matrici. Si tratta delle matrici (Mab)=(Mab)=M, dove M è la matrice 2×2 seguente:
[7] formula,
dove i2=−1. Si noti che MM=I, dove I è la matrice identità. Queste matrici rappresentano la coppa e il cappello nel senso seguente: le particelle possono avere due colori (chiamiamoli 0 e 1) e allora Mab e Mab rappresentano l'ampiezza di probabilità per la creazione simultanea e per l'annichilazione reciproca, rispettivamente, di due particelle con colore a e b. La condizione MM=I è richiesta dalla topologia, come illustrato dalle relazioni
[8] formula.
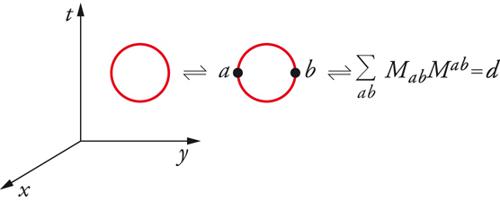
Si noti che l'ampiezza del cerchio risulta essere:
[9] ∑ MabMab = ∑ MabMab =∑ M2ab =
= (iA)2 + (−iA−1)2 = −A2 −A−2
come illustrato nella fig. 13. Definiamo ora una matrice R tramite l'equazione:
[10] Rcdab = AMabMcd + AIca Idb
dove Ica denota la matrice identità. Possiamo anche definire la matrice R diagrammaticamente nel modo seguente:
[11] formula
Dunque diagrammaticamente identifichiamo R con l'incrocio (fig. 2A) e, quindi, l'equazione che definisce R si può riscrivere simbolicamente nella forma:
[12] formula
Questa equazione, presa insieme al valore −A2−A−2 dell'anello chiuso, può essere vista come un algoritmo ricorrente per il calcolo dell'ampiezza e in questa forma ritroviamo il modello del bracket come somma sugli stati per il polinomio di Jones (non normalizzato). Da questo modo di intendere un invariante di nodo come ampiezza quantistica segue una ricca teoria dei nodi legata alla fisica teorica. Si tratta di sviluppi ancora in corso e la speranza è che, attraverso questa teoria, la fisica e la matematica possano aiutarsi a vicenda e progredire parallelamente.
La vita propria della notazione e l'integrale di Feynman
La notazione di Dirac è dotata di vita propria. Sia
[13] P = ∣y⟩ ⟨x∣ , ⟨x ∣∣y⟩ = ⟨x ∣y⟩.
Allora
[14] PP= ∣y⟩ ⟨x∣∣y⟩ ⟨x∣= ∣y⟩ ⟨x∣y⟩ ⟨x∣=⟨x∣y⟩P.
A meno di moltiplicazione per uno scalare, P è un operatore di proiezione. In questo linguaggio, la completezza di un determinato insieme di stati intermedi si esprime con il fatto che una certa somma di proiezioni sia l'identità. Infatti, supponiamo che
Allora si ha:
[16] formula.
Illustriamo ora come l'iterazione di questo processo di espansione su un insieme di stati completo conduca alla forma più primitiva dell'integrale di Feynman. Immaginiamo che lo stato iniziale a e quello finale b definiscano punti rispettivamente delle rette x=0 e x=n+1 del piano (x,y) e che (k,c(k)j(k)) sia un dato punto (stato) sulla retta x=k per k=1,…,n e 0⟨j(k)≤m, in modo tale che la somma dei proiettori in ogni livello intermedio sia completa. Supponiamo cioè che la somma seguente risulti sempre uguale a 1 per k che varia da 1 a n:
[17] ∣c(k)1⟩ ⟨c(k)1∣+...+∣c(k)m⟩ ⟨c(k)m∣=1.
Applicando la condizione di completezza iterativamente si ottiene allora, per l'ampiezza ⟨a∣b⟩, la seguente espressione:
[18] ⟨a∣b⟩ =∑ ∑ ...∑ ⟨a∣c(1)j(1)⟩⟨c(1)j(1)∣c(2)j(2)⟩
⟨c(2)j(2)∣c(3)j(3)⟩...⟨c(n−1)j(n−1)∣c(n)j(n)⟩⟨c(n)j(n)∣b⟩
in cui la somma è eseguita su tutti i valori di j(k) tra 1 e m, mentre k varia da 1 a n. Ciascuno dei termini della somma può essere pensato come un cammino combinatorio da a a b nello spazio bidimensionale del piano (x,y). Pertanto, l'ampiezza di probabilità della transizione da a a b risulta uguale alla somma dei contributi di tutti i cammini che uniscono a e b. Richard P. Feynman utilizzò questa descrizione per ottenere il suo famoso integrale sui cammini per l'espressione delle ampiezze in meccanica quantistica. Questo integrale prende la forma
[19] ∫dPexp(iS).
L'integrale è eseguito su tutti i cammini dal punto a al punto b e S è l'azione associata al fatto che una particella viaggi da a a b secondo un certo cammino. Per la meccanica quantistica associata a una particella classica (newtoniana), l'azione S è data dall'integrale lungo il cammino della differenza T−V, dove T e V sono rispettivamente l'energia cinetica e l'energia potenziale classiche della particella. L'eleganza dell'approccio di Feynman alla meccanica quantistica risiede nella straordinaria chiarezza con cui fa emergere il rapporto tra il punto di vista classico e quello quantistico. Il moto classico corrisponde alle regioni dove tutti i cammini tra loro vicini contribuiscono costruttivamente alla somma e, dunque, il corrispettivo cammino corrisponde alla variazione nulla dell'azione. La ricerca dei cammini per cui la variazione di azione è nulla è un tipico problema del calcolo delle variazioni e conduce direttamente alle equazioni del moto di Newton. Dunque, tramite un'opportuna scelta dell'azione, il punto di vista classico e quello quantistico risultano unificati.
La debolezza di questo approccio sta nel fatto che sino a ora non è stata sviluppata una teoria della misura adatta a formalizzare l'integrale di Feynman in tutte le situazioni possibili. In conclusione, la notazione di Dirac pone in risalto il legame tra l'interpretazione probabilistica dell'ampiezza e la struttura di spazio vettoriale dello spazio degli stati di un sistema quantistico. La strategia che utilizzeremo nel seguito per mettere in evidenza le relazioni tra la teoria dei quanti e la topologia ruota intorno al bracket di Dirac, che funge da intermediario tra la notazione e l'algebra lineare. Dunque la connessione tra la meccanica quantistica e la topologia si ottiene effettivamente estendendo la notazione di Dirac.
Teoria topologica dei campi: primi passi
Per giustificare l'idea dell'estensione della notazione di Dirac, consideriamo il seguente scenario. Sia M una varietà tridimensionale e sia F una superficie chiusa orientata in M, che divide M in due parti, M1 e M2; queste due parti sono varietà tridimensionali con bordo, che si incontrano lungo F. Consideriamo ora un'ampiezza ⟨M1∣M2⟩=Z(M), la cui forma sia una generalizzazione delle considerazioni precedenti in questo senso: la superficie F introduce la distinzione tra le parti M1 e M2, e consente di interpretarle rispettivamente come preparazione e risultato. Possiamo dire che si tratta di una generalizzazione dell'ampiezza di Dirac ⟨a∣b⟩, in cui la linea verticale rappresenta uno strumento di distinzione topologica nello spazio M. Se Z(M) è un invariante topologico di M essa viene chiamata ampiezza topologica; si noti che l'ampiezza topologica non dipende dalla superficie F che divide M.
Dal punto di vista fisico l'indipendenza dell'ampiezza topologica dalla particolare superficie di divisione delle 3-varietà è la proprietà più importante. Nelle 3-varietà viene introdotta la distinzione tra due parti e l'ampiezza emerge interpretandone una come osservatore e l'altra come osservato. Se l'ampiezza deve fornire informazioni fisiche (ovvero topologiche) sulla sottostante varietà, allora non deve dipendere dalla particolare suddivisione in osservatore e osservato. Le stesse considerazioni si applicano alle varietà di dimensione quattro e hanno stretti rapporti con la teoria della relatività. La questione delle ampiezze quadridimensionali è attualmente oggetto di ricerca, mentre nel caso tridimensionale sono già noti numerosi esempi di ampiezza topologica; per questo ci siamo concentrati soprattutto su tale caso. Notiamo ancora però che l'idea che un'ampiezza debba essere indipendente dalla distinzione che la produce è antecedente alla topologia. L'invarianza topologica delle ampiezze è un modo comodo e fondamentale per produrre questa indipendenza.
L'improvviso emergere del concetto di ampiezza topologica ha il suo complemento nella fisica matematica. Witten ha proposto un modello per la costruzione di una classe di invarianti di 3-varietà, consistente in integrali di Feynman generalizzati della forma seguente:
[20] formula.
In questa espressione M denota una 3-varietà senza bordo e A è un campo di gauge (detto anche potenziale di gauge o connessione di gauge) definito su M. Il campo di gauge è una 1-forma su M a valori in una rappresentazione di un'algebra di Lie e il gruppo di Lie corrispondente a tale algebra è detto gruppo di gauge del campo. Nell'integrale si considera come azione S(M,A) l'integrale su M della traccia della 3-forma di Chern-Simons,
[21] formula,
dove il prodotto è il prodotto esterno di forme differenziali. Invece che essere esteso a tutti i cammini, l'integrale che compare in Z(M) è calcolato su tutti i campi di gauge a meno di equivalenza di gauge. L'espressione formale dell'integrale e la sua logica interna hanno fatto ritenere che nel modello proposto esista un'ampia classe di invarianti topologici di varietà tridimensionali e, associati a essi, anche invarianti di nodi e linkin 3-varietà.
In effetti sono state trovate rigorose descrizioni combinatorie degli invarianti associati a questo integrale. Restano tuttavia ancora aperte domande e congetture di notevole interesse legate alla formulazione degli invarianti come integrali. Inoltre, molti problemi affascinanti sono scaturiti dall'introduzione dell'integrale funzionale di Witten. Notiamo che a questo integrale si possono dare interpretazioni fisiche e da queste interpretazioni dedurre risultati che forniscono approssimazioni dell'effettivo comportamento dell'integrale. Questo processo è del tutto analogo all'approssimazione con cui si ottiene la meccanica classica come caso limite dell'usuale integrale sui cammini di Feynman. Questa cosiddetta approssimazione di fase stazionaria suggerisce una straordinaria serie di congetture sul comportamento delle versioni dell'integrale definite in modo rigoroso, e queste congetture sono state in effetti verificate numericamente in molti casi particolari.
Bibliografia
Dirac 1958: Dirac, Paul A.M., The principles of quantum mechanics, 4. ed., Oxford, Clarendon, 1958 (1. ed.: 1930).
Feynman, Hibbs 1965: Feynman, Richard P. - Hibbs, Albert R., Quantum mechanics and path integrals, New York, McGraw-Hill, 1965.
Freed 1991: Freed, Daniel S. - Gompf, Robert E., Computer calculations of Witten's 3-manifold invariants, "Communications in mathematical physics", 141, 1991, pp. 79-117.
Jones 1983: Jones, Vaughan F.R., Index for subfactors, "Inventiones mathematicae", 72, 1983, pp. 1-25.
Jones 1985: Jones, Vaughan F.R., A polynomial invariant for links via von Neumann algebras, "Bulletin of the American Mathematical Society", 12, 1985, pp. 103-112.
Kauffman 1983: Kauffman, Louis H., Formal knot theory, Princeton (N.J.), Princeton University Press, 1983.
Kauffman 1987: Kauffman, Louis H., State models and the Jones polynomial, "Topology", 26, 1987, pp. 395-407.
Kauffman 1990: Kauffman, Louis H., Statistical mechanics and the Jones polynomial, in: New problems, methods and techniques in quantum field theory and statistical mechanics, edited by Mario G. Rasetti, Singapore-London, World Scientific, 1990, pp. 175-222.
Kauffman 1994: Kauffman, Louis H. - Lins, Sóstenes L., Temperley-Lieb recoupling theory and invariants of 3-manifolds, Princeton (N.J.), Princeton University Press, 1994.
Murasugi 1987: Murasugi, Kunio, The Jones polynomial and classical conjectures in knot theory, "Topology", 26, 1987, pp. 297-307.
Reidemeister 1932: Reidmeister, Kurt, Knotentheorie, Berlin, Springer, 1932.
Reshetikhin, Turaev 1991: Reshetikhin, Nicolai Y. - Turaev, Vladimir G., Invariants of 3-manifolds via link polynomials and quantum groups, "Inventiones mathematicae", 103, 1991, pp. 547-597.
Tait 1898: Tait, Peter G., On knots I, II, III, in: Scientific papers, Cambridge, Cambridge University Press, 1898-1900, 2 v.; v. I, pp. 273-347.
Thomson (Lord Kelvin) 1867: Thomson, William, On vortex atoms, "Philosophical magazine", 34, 1867, pp. 15-24.
Turaev, Viro: 1992: Turaev, Vladimir G. - Viro, Oleg Y., State sum invariants of 3-manifolds and quantum 6j symbols, ‟Topology", 31, 1992, pp. 865-902.
Witten 1989: Witten, Edward, Quantum field theory and the Jones polynomial, "Communications in mathematical physics", 121, 1989, pp. 351-399.