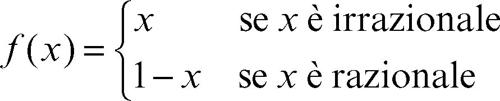monotonia
monotonia
monotonia termine utilizzato per indicare genericamente la proprietà di una funzione o di una successione di essere crescente o decrescente. Più precisamente, una funzione definita in un insieme ordinato E a valori in un insieme ordinato F è monotona se per ogni coppia di punti x1 e x2 di E, con x1 < x2, si ha ƒ(x1) ≤ ƒ(x2) (ƒ è una funzione crescente anche detta a volte monotona non decrescente), oppure ƒ(x2) ≤ ƒ(x1) (ƒ è una funzione decrescente anche detta a volte monotona non crescente). Per una funzione reale di variabile reale si parla di monotonia stretta quando le disuguaglianze sono strette e allora la funzione è rispettivamente strettamente crescente o decrescente.
L’ipotesi di monotonia stretta di una funzione garantisce l’esistenza della sua funzione inversa. Tuttavia è una condizione solo sufficiente, come mostra l’esempio della funzione così definita per casi:
Questa funzione, infatti, è invertibile in R senza essere monotona su alcun intervallo. Per funzioni continue in un intervallo [a, b], tuttavia, la monotonia è anche necessaria per l’invertibilità. L’ipotesi di monotonia è inoltre una semplice ipotesi che garantisce l’esistenza del limite (finito o infinito) per x tendente a ±∞. Una funzione monotona in un intervallo [a, b] ammette solo discontinuità di prima specie (cioè dei salti), in numero finito o numerabile di punti. La nozione di monotonia per una successione di numeri reali è analoga: la successione {an} è monotona crescente (decrescente) se risulta an ≤ an+1 (an ≥ an+1) per ogni numero naturale n. Anche in questo caso se le disuguaglianze sono strette, sarà tale anche la monotonia crescente o decrescente. Le successioni monotone sono regolari, ossia ammettono limite, finito o infinito.